第十四章 整式的乘法和因式分解 单元测试----初中数学人教版八年级上册
试卷更新日期:2021-11-14 类型:单元试卷
一、单选题
-
1. (﹣3)0等于( )A、0 B、1 C、3 D、﹣32. 计算(a+3)(﹣a+1)的结果是( )A、﹣a2﹣2a+3 B、﹣a2+4a+3 C、﹣a2+4a﹣3 D、a2﹣2a﹣33. 下列各式由左到右的变形中,属于因式分解的是( )A、a(m+n)=am+an B、a2﹣b2﹣c2=(a+b(a﹣b)﹣c2 C、10x2﹣5x=5x(2x﹣1) D、x2﹣16+6x=(x+4)(x﹣4)+6x4. 如果(x-4)(x+3)=x2+mx-12,则m的值为( )A、1 B、-1 C、7 D、-75. 如图,现有足够多的型号为①②③的正方形和长方形卡片,如果分别选取这三种型号卡片若干张,可以拼成一个不重叠、无缝隙的长方形,小星想用拼图前后面积之间的关系.解释多项式乘法 ,则其中②和③型号卡片需要的张数各是( )
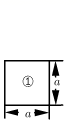

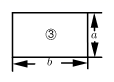 A、3张和7张 B、2张和3张 C、5张和7张 D、2张和7张6. 若 ,则 的值是( )A、 B、 C、 D、7. 若 的乘积中不含 项,则 的值为( )A、5 B、 C、 D、-58. 为了求 的值,可设 ,等式两边同乘以 ,得 ,所以得 ,所以 ,即: = .仿照以上方法求 的值为( )A、 B、 C、 D、9. 在矩形ABCD内,将两张边长分别为a和b( )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为 ,图2中阴影部分的面积为 .当 时, 的值是( )
A、3张和7张 B、2张和3张 C、5张和7张 D、2张和7张6. 若 ,则 的值是( )A、 B、 C、 D、7. 若 的乘积中不含 项,则 的值为( )A、5 B、 C、 D、-58. 为了求 的值,可设 ,等式两边同乘以 ,得 ,所以得 ,所以 ,即: = .仿照以上方法求 的值为( )A、 B、 C、 D、9. 在矩形ABCD内,将两张边长分别为a和b( )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为 ,图2中阴影部分的面积为 .当 时, 的值是( )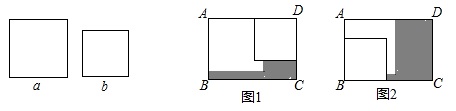 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 分解因式: .11. 若 ,则 .12. 若 , ,则代数式 的值等于 .13. 公元9世纪,阿拉伯数学家阿尔•花拉子米在他的名著《代数学》中用图解一元二次方程,他把一元二次方程 写成 的形式,并将方程左边的 看作是由一个正方形(边长为 )和两个同样的矩形(一边长为 ,另一边长为 )构成的矩尺形,它的面积为 ,如图所示.于是只要在这个图形上添加一个小正方形,即可得到一个完整的大正方形,这个大正方形的面积可以表小为: ,整理,得 ,因为 表示边长,所以 .

三、计算题
-
14. 计算:(1)、(-a3)2·a3-4a2·a7(2)、(2a+1)(-2a+1)
四、解答题