14.2.2 完全平方公式 同步练习----初中数学人教版八年级上册
试卷更新日期:2021-11-14 类型:同步测试
一、单选题
-
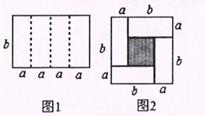
1. 下列运算中,计算正确的是( )A、(﹣2b2)3=﹣8b6 B、4a4÷2a2=2a C、2a•4a=8a D、(a+b)2=a2+b22. 若 , ,则 ( )A、5 B、10 C、13 D、223. 已知 , , ,那么 的值等于( )A、0 B、1 C、2 D、34. 已知 ,则代数式 的值是A、 B、 C、 D、5. 如图,有三种规格的卡片共25张,其中边长为a的正方形卡片9张,边长为b的正方形卡片4张,长,宽分别为a,b的长方形卡片12张,现使用这25张卡片拼成一个大的正方形,则这个大正方形的边长为( )
 A、 B、 C、 D、6. 若多项式 是一个完全平方式,则m的值为( )A、12 B、±12 C、6 D、±67. 观察“赵爽弦图”(如图),若图中四个全等的直角三角形的两直角边分别为a , b , ,根据图中图形面积之间的关系及勾股定理,可直接得到等式( )
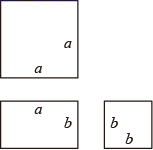
A、 B、 C、 D、6. 若多项式 是一个完全平方式,则m的值为( )A、12 B、±12 C、6 D、±67. 观察“赵爽弦图”(如图),若图中四个全等的直角三角形的两直角边分别为a , b , ,根据图中图形面积之间的关系及勾股定理,可直接得到等式( ) A、 B、 C、 D、8. 不论x、y为什么实数,代数式x2+y2+2x﹣4y+7的值( )A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数
A、 B、 C、 D、8. 不论x、y为什么实数,代数式x2+y2+2x﹣4y+7的值( )A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数二、填空题
-
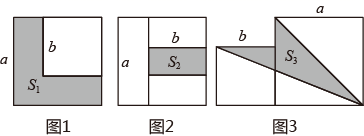
9. 计算 的结果为10. 已知a﹣b=7,ab=2,则(a+b)2= .11. 如果代数式x2+mx+9=(x+b)2 , 那么m的值为.12. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为 ;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为 .若 ,则 + = ;当 + =40时,则图3中阴影部分的面积 .
三、解答题