14.2.1 平方差的公式 同步练习----初中数学人教版八年级上册
试卷更新日期：2021-11-14 类型：同步测试
一、单选题
-
1. 下列运算一定正确的是（ ）.A、 B、 C、 D、2. 在下列各式中，一定能用平方差公式因式分解的是（ ）．A、 B、 C、 D、3. 如果一个数等于两个连续奇数的平方差，那么我们称这个数为“幸福数”.下列数中为“幸福数”的是（ ）A、205 B、250 C、502 D、5204. 记 则x+1=（ ）A、一个奇数 B、一个质数 C、一个整数的平方 D、一个整数的立方5. 如图，阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形，小佳将阴影部分通过剪拼，拼成了图①、图②、图③三种新的图形，其中能够验证平方差公式的是（ ）
A、①② B、①③ C、②③ D、①②③6. 用简便方法计算，将98×102变形正确的是（ ）A、98×102＝1002+22 B、98×102＝（100﹣2）2 C、98×102＝1002﹣22 D、98×102＝（100+2）27. 若A＝(2＋1)(22＋1)(24＋1)(28＋1)＋1，则A的末位数字是（ ）A、2 B、4 C、6 D、88. 如图，大正方形的边长为 ，小正方形的边长为 ， ， 表示四个相同长方形的两边长（ ）.则① ；② ；③ ；④ ，中正确的是（ ）
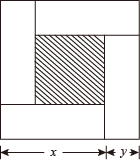A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
9. 计算 ．10. 当a＝﹣1时，代数式（2a+1）（2a﹣1）＝.11. 如图1，将边长为a的大正方形剪去一个边长为b的小正方形，并沿图中的虚线剪开，拼接后得到图2，请根据图形的面积写出一个含字母a，b的等式.
12. 若代数式x2-a在有理数范围内可以因式分解，则整数a的值可以为（写出一个即可）13. 定义：若一个正整数能表示为两个连续自然数的平方差，那么就称这个正整数为“平方差数”.例如： ，因此1，3，5这三个数都是“平方差数”.则不大于200的所有“平方差数”之和为.14. 将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限，如图中方式叠放，则按图示规律排列的所有阴影部分的面积之和为.
三、解答题
-
15. 如图所示，小刚家门口的商店在装修，他发现工人正在一块半径为R的圆形板材上，冲去半径为r的四个小圆，小刚测得R＝6.8dm，r＝1.6dm，他想知道剩余阴影部分的面积，你能利用所学过的因式分解的知识帮助小刚计算吗？请写出求解过程（结果保留π）.
16. 能被2整除的数叫做偶数，不能被2整除的整数叫做奇数．引入负数后，如1，-3等是奇数，0，-2等是偶数．任意两个连续整数的平方差能确定是奇数还是偶数吗？写出你的判断并证明．四、综合题
-
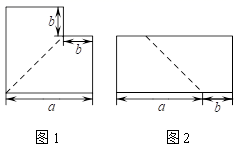
17. 乘法公式的探究及应用.
(1)、如图1，可以求出阴影部分的面积是 （写成两数平方差的形式）；(2)、如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是 ， 长是 ， 面积是.（写成多项式乘法的形式）(3)、比较两图的阴影部分面积，可以得到乘法公式.（用式子表达）(4)、运用你所得到的公式，计算下列各题：①10.3×9.7；
②（2m+n﹣p）（2m﹣n+p）.