浙教版数学九上第4章 相似三角形优生综合题特训
试卷更新日期:2021-11-13 类型:复习试卷
一、综合题
-
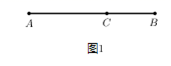
1. 如图1所示,点C把线段 分成 与 ,若 ,则称线段 被点C黄金分割(goldensection),点C叫做线段 的黄金分割点, 与 的比叫做黄金比.
 (1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C .
(1)、根据上述定义求黄金比;(2)、在图2中,利用尺规按以下步骤作图,井保留作图痕迹.①作线段 的垂直平分线,得线段 的中点M;②过点B作 垂线l;③以点B为圆心,以 为半径作圆交l于N;④连接 、 ,以N为圆心,以 为半径作圆交 于P;⑤以点A为圆心,以 为半径作圆交 于C . (3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.2. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.
(3)、证明你按以上步骤作出的C点就是线段 的黄金分割点.2. 定义:如图1,点P为线段AB上一点,如果 =k,那么我们称点P是线段AB的黄金分割点, 叫做黄金分割数.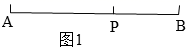
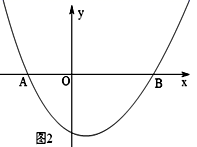 (1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.3. 如图,在一块长为a(cm),宽为b(cm)(a>b)的矩形黑板的四周,镶上宽为x(cm)的木板,得到一个新的矩形.
(1)、理解:利用图1,运用一元二次方程的知识,求证:黄金分割数 ;(2)、应用:如图2,抛物线y=x2+nx+2n(n<0)的图象与x轴交于A、B两点(OA<OB),若原点O是线段AB的黄金分割点,①求线段AB的长;②直接写出点A和点B的坐标.3. 如图,在一块长为a(cm),宽为b(cm)(a>b)的矩形黑板的四周,镶上宽为x(cm)的木板,得到一个新的矩形.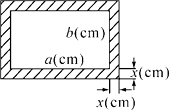 (1)、试用含a,b,x的代数式表示新矩形的长和宽;
(1)、试用含a,b,x的代数式表示新矩形的长和宽;
(2)、试判断原矩形的长、宽与新矩形的长、宽是不是比例线段,并说明理由.
4. 已知线段a,b,c满足 ,且a+2b+c=26.(1)、判断a,2b,c,b2是否成比例;(2)、若实数x为a,b的比例中项,求x的值.5. (问题情境)如图①,小区 、 位于一条笔直的道路 的同侧,为了方便 , 两个小区居民投放垃圾,现在 上建一个垃圾分类站 ,使得 与 , 的距离之比为 .
 (1)、(初步研究)
(1)、(初步研究)
在线段 上作出点 ,使 .如图,做法如下:

第一步:过点 作射线 ,
以 为圆心,任意长为半径画弧,交 于点 ;
以 为圆心, 长为半径画弧,交 于点 ;
以 为圆心, 长为半径画弧,交 于点 .
第二步:连接 ,作 ,交 于点 .
则点 即为所求.
请证明所作的点 满足 .
(2)、(深入思考)
如图,点 在线段 上,点 在直线 外,且 .求证: 是 的平分线.
 (3)、(问题解决)
(3)、(问题解决)
如图,已知点 , 和直线 ,点 在线段 上,且 .用直尺和圆规完成下列作图.(保留作图痕迹,不写作法)(ⅰ)在直线 上作出点 (异于点 ),使 ;
(ⅱ)在直线 上作出点 ,使 .
 6. 如图,已知等边 ,在 , 边分别取点 , ,使 ,连接 , 相交于点 .
6. 如图,已知等边 ,在 , 边分别取点 , ,使 ,连接 , 相交于点 .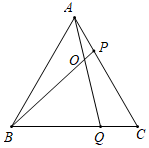 (1)、求证: ≌ .(2)、若 .
(1)、求证: ≌ .(2)、若 .①求 的值.
②设 的面积为 ,四边形 的面积为 ,求 的值.
7. 如图,在平面直角坐标系中,抛物线 : 经过点 和 . (1)、求抛物线 的对称轴.(2)、当 时,将抛物线 向左平移2个单位,再向下平移1个单位,得到抛物线 .
(1)、求抛物线 的对称轴.(2)、当 时,将抛物线 向左平移2个单位,再向下平移1个单位,得到抛物线 .①求抛物线 的解析式.
②设抛物线 与 轴交于 , 两点(点 在点 的右侧),与 轴交于点 ,连接 .点 为第一象限内抛物线 上一动点,过点 作 于点 .设点 的横坐标为 .是否存在点 ,使得以点 , , 为顶点的三角形与 相似,若存在,求出 的值;若不存在,请说明理由.
8. 已知一次函数 的图象与反比例函数 的图象在第一象限交于点 ,与 轴交于点 ,与 轴交于点 ,若 ,且 . (1)、求反比例函数与一次函数的解析式;(2)、直接写出 的解集;(3)、若点 为 轴上一点,求使 的点 的坐标.9. 综合问题:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)、求反比例函数与一次函数的解析式;(2)、直接写出 的解集;(3)、若点 为 轴上一点,求使 的点 的坐标.9. 综合问题:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线. (1)、如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.(2)、在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.(3)、如图2,△ABC中,AC=2,DC= - ,BD= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求CB长.10. 如图,一次函数 的图象与反比例函数 的图象交于点 、 两点,与 轴、 轴分别交于 、 两点,且点 的坐标为 .
(1)、如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.(2)、在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.(3)、如图2,△ABC中,AC=2,DC= - ,BD= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求CB长.10. 如图,一次函数 的图象与反比例函数 的图象交于点 、 两点,与 轴、 轴分别交于 、 两点,且点 的坐标为 .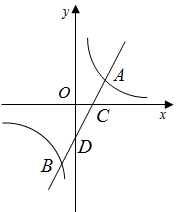 (1)、求一次函数和反比例函数的表达式.(2)、求 的面积.(3)、点 为反比例函数图象上的一个动点, 轴于 ,是否存在以 、 、 为顶点的三角形与 相似,若存在,直接写出 点的坐标,若不存在,请说明理由.11. 如图所示,在平面直角坐标系中,点 的坐标为 ,动点 在 轴上,点 是线段 的中点.将线段 绕着点 顺时针方向旋转 ,得到线段 ,连结 、 .
(1)、求一次函数和反比例函数的表达式.(2)、求 的面积.(3)、点 为反比例函数图象上的一个动点, 轴于 ,是否存在以 、 、 为顶点的三角形与 相似,若存在,直接写出 点的坐标,若不存在,请说明理由.11. 如图所示,在平面直角坐标系中,点 的坐标为 ,动点 在 轴上,点 是线段 的中点.将线段 绕着点 顺时针方向旋转 ,得到线段 ,连结 、 . (1)、写出点 的坐标;(2)、当 时,试问:以 为顶点的四边形能否为平行四边形?若能,求出相应的 的值?若不能,请说明理由;(3)、当 为何值时,△ 与△ 相似?12. 如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
(1)、写出点 的坐标;(2)、当 时,试问:以 为顶点的四边形能否为平行四边形?若能,求出相应的 的值?若不能,请说明理由;(3)、当 为何值时,△ 与△ 相似?12. 如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB. (1)、求 的值.(2)、若E为x轴上的点,且S△AOE= ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?(3)、若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.13. 在平面直角坐标系中,抛物线 ( )与 轴的两个交点分别为A、B,与 轴相交于点C,点A( ,0), ,连接BC,tan∠OCB=2.
(1)、求 的值.(2)、若E为x轴上的点,且S△AOE= ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?(3)、若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.13. 在平面直角坐标系中,抛物线 ( )与 轴的两个交点分别为A、B,与 轴相交于点C,点A( ,0), ,连接BC,tan∠OCB=2. (1)、求该抛物线的解析式;(2)、设点P是抛物线上在第一象限内的动点(不与C、B重合),过点P做PD⊥BC,垂足为点D.
(1)、求该抛物线的解析式;(2)、设点P是抛物线上在第一象限内的动点(不与C、B重合),过点P做PD⊥BC,垂足为点D.①点P在运动过程中,线段PD的长度是否存在最大值?若存在,请求出点D的坐标;若不存在,请说明理由;
②以P、D、C为顶点的三角形与△COA相似时,求出点P的坐标.
14. 如图在平面直角坐标系中,点O为坐标原点,直线y x+b分别交x轴,y轴于点A、B , OA=4,∠OBA的外角平分线交x轴于点D .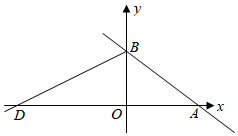 (1)、求点D的坐标;(2)、点P是线段BD上一点(不与B、D重合),过点P作PC⊥BD交x轴于点C , 设点P的横坐标为t , △BCD的面积为S , 求S与t之间的函数解析式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,PC的延长线交y轴于点E , 当PC=PB时,将射线EP绕点E旋转45°交直线AB于点F , 求F点坐标.15. 已知正方形 中,点 是边 上一点(不与 、 重合),将 绕点 顺时针旋转 得到 ,如图1,连接 ,分别交 、 于点 、 .
(1)、求点D的坐标;(2)、点P是线段BD上一点(不与B、D重合),过点P作PC⊥BD交x轴于点C , 设点P的横坐标为t , △BCD的面积为S , 求S与t之间的函数解析式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,PC的延长线交y轴于点E , 当PC=PB时,将射线EP绕点E旋转45°交直线AB于点F , 求F点坐标.15. 已知正方形 中,点 是边 上一点(不与 、 重合),将 绕点 顺时针旋转 得到 ,如图1,连接 ,分别交 、 于点 、 .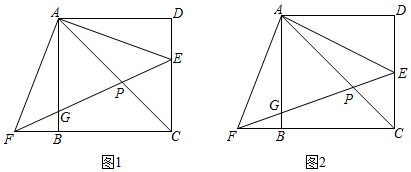 (1)、求证: ;(2)、求证: ;(3)、如图2,当点 是边 的中点时, ,求 的长.16. 如图,已知抛物线 的图象与 轴交于 , 两点,与 轴交于点 ,抛物线的对称轴与 轴交于点 .点 从 点出发,以每秒1个单位长度的速度向 运动,过 作 轴的垂线,交抛物线于点 ,交 于 .
(1)、求证: ;(2)、求证: ;(3)、如图2,当点 是边 的中点时, ,求 的长.16. 如图,已知抛物线 的图象与 轴交于 , 两点,与 轴交于点 ,抛物线的对称轴与 轴交于点 .点 从 点出发,以每秒1个单位长度的速度向 运动,过 作 轴的垂线,交抛物线于点 ,交 于 . (1)、求点 和点 的坐标;(2)、设当点 运动了 (秒 时,四边形 的面积为 ,求 与 的函数关系式,并指出自变量 的取值范围;(3)、在线段 上是否存在点 ,使得 成为以 为一腰的等腰三角形?若存在,求出点 的坐标,若不存在,说明理由.17. 学完“探索三角形相似的条件”之后,小明所在的学习小组尝试探索四边形相似的条件,以下是他们的思考,请你和他们一起完成探究过程.
(1)、求点 和点 的坐标;(2)、设当点 运动了 (秒 时,四边形 的面积为 ,求 与 的函数关系式,并指出自变量 的取值范围;(3)、在线段 上是否存在点 ,使得 成为以 为一腰的等腰三角形?若存在,求出点 的坐标,若不存在,说明理由.17. 学完“探索三角形相似的条件”之后,小明所在的学习小组尝试探索四边形相似的条件,以下是他们的思考,请你和他们一起完成探究过程.(定义)四边成比例,且四角分别相等的两个四边形叫做相似四边形.
(1)、(初步思考)小明根据探索三角形相似的条件所获得的经验,考虑可以从定义出发逐步弱化条件探究四边形相似的条件.他考虑到“四角分别相等的两个四边形相似”可以举出反例“矩形”,“四边成比例的两个四边形相似”可以举出反例.所以四边形相似的条件必须再添加条件,于是,可以从“四边成比例,且一角对应相等的两个四边形相似”,“三边成比例,且两角分别相等的两个四边形相似”,“两边成比例,且三角分别相等的两个四边形相似”来探究.
(2)、(深入探究)学习小组一致认为,“四边成比例,且一角对应相等的两个四边形相似”是真命题,请结合图形完成证明.
已知:四边形 和四边形 中, , .
求证:四边形 四边形 .证明:
 (3)、对于“三边成比例,且两角分别相等的两个四边形相似”,学习小组得到如下的四个命题:
(3)、对于“三边成比例,且两角分别相等的两个四边形相似”,学习小组得到如下的四个命题:①“三边成比例,两邻角分别相等且只有一角为其中两边的夹角的两个四边形相似”;
②“三边成比例,两邻角分别相等且都不是其中两边的夹角的两个四边形相似”;
③“三边成比例及其两夹角分别相等的两个四边形相似”;
④“三边成比例,两对角分别相等的两个四边形相似”.
其中真命题是.(填写所有真命题的序号)
(4)、请你完成“两边成比例,且三角分别相等的两个四边形相似”的探究过程.18. 如图所示,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,其对称轴 与 轴相交于点 ,点 为抛物线的顶点. (1)、求抛物线的表达式.(2)、若直线 交 轴于点 ,求证: .(3)、若点 是线段 上的一个动点,是否存在以点 、 、 为顶点的三角形与 相似.若存在,求出点 的坐标;若不存在,请说明理由.19. 如图, 中, ,P是斜边 上一个动点,以 为直径作 交 于点D,与 的另一个交点E,连接 .
(1)、求抛物线的表达式.(2)、若直线 交 轴于点 ,求证: .(3)、若点 是线段 上的一个动点,是否存在以点 、 、 为顶点的三角形与 相似.若存在,求出点 的坐标;若不存在,请说明理由.19. 如图, 中, ,P是斜边 上一个动点,以 为直径作 交 于点D,与 的另一个交点E,连接 .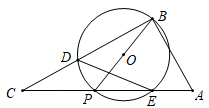 (1)、当 时,
(1)、当 时,①若 ,求 的度数;
②求证 ;
(2)、当 , 时,是否存在点P,使得 是等腰三角形,若存在,求出所有符合条件的 的长.20. 如图,点 的坐标为 ,点 的坐标为①以点 为旋转中心,将 顺时针方向旋转90°,得到 ;
②以点 为位似中心,将 放大 ,使相似比为 ,且点 在第三象限.
(1)、在图中画出 和 ;(2)、请直接写出点 的坐标:( , )(3)、在上面的(2)问下,直接写出在线段 上的任意动点 的对应点 的坐标:( , ). 21. (1)在正方形方格纸中,我们把顶点均在“格点”上的三角形称为“格点三角形”,如图△ABC是一个格点三角形,点A的坐标为(-2,2).
21. (1)在正方形方格纸中,我们把顶点均在“格点”上的三角形称为“格点三角形”,如图△ABC是一个格点三角形,点A的坐标为(-2,2). (1)、点B的坐标为 , △ABC的面积为;(2)、在所给的方格纸中,请你以原点O为位似中心,将△ABC缩小为原来的一半(仅用直尺);(3)、在(2)中,若P(a,b)为线段AC上的任一点,则缩小后点P的对应点P1的坐标为.(4)、按要求作图,不要求写作法,但要保留作图痕迹.
(1)、点B的坐标为 , △ABC的面积为;(2)、在所给的方格纸中,请你以原点O为位似中心,将△ABC缩小为原来的一半(仅用直尺);(3)、在(2)中,若P(a,b)为线段AC上的任一点,则缩小后点P的对应点P1的坐标为.(4)、按要求作图,不要求写作法,但要保留作图痕迹.我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.
请运用上述性质,只用直尺(不带刻度)作图.
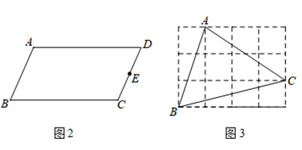
①如图2,在平行四边形ABCD中,E为CD的中点,作BC的中点F.
②如图3,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH.
 22. 如图所示,身高1.5米的小明从路灯下的A点经过,测量得身后的影子 的长5米,沿 所在的直线行走10米到B点时,身后的影子 长为2米.
22. 如图所示,身高1.5米的小明从路灯下的A点经过,测量得身后的影子 的长5米,沿 所在的直线行走10米到B点时,身后的影子 长为2米. (1)、请你确定路灯P的位置(2)、求路灯P距到地面的距离.23. 以下是一个合作学习小组在一次数学实验中的过程记录,请阅读后完成下列问题.(1)、(度量操作)
(1)、请你确定路灯P的位置(2)、求路灯P距到地面的距离.23. 以下是一个合作学习小组在一次数学实验中的过程记录,请阅读后完成下列问题.(1)、(度量操作)如图1,AB⊥PQ ,垂足为A,AB=3,E为射线AQ上一个动点(点E与点A不重合),∠AEB=∠BEC,BC⊥BE,过点C作CD⊥PQ,垂足为点D.在探究线段AB、线段AE、线段AD三者之间的关系时,通过画图、度量,收集到一组数据如下表:(单位:cm)

AE
1
1.5
1.8
2
2.25
3
4
4.5
5
AD
9
6
5
4.5
4
3
2.25
2
1.8
根据学习函数的经验,选取上表中 和 的数据进行分析:
①设 , ,以 为坐标,在图2所示的坐标系中描出对应的点;
②连线.
(2)、(观察思考)结合表中的数据,猜想:当AB=3时, .
(3)、进一步猜想:AB⊥PQ,垂足为A,E为射线AQ上一个动点(点E与点A不重合),∠AEB=∠BEC,BC⊥BE,过点C作CD⊥PQ,垂足为点D.则线段AB、AE、AD三者之间的关系为.(4)、(推理证明)请利用图1证明上述(4)中的猜想.
(5)、(逆向运用)如图3为一张四边形ABCD纸片,∠BAD=∠ADC=90°, , AD=2,请通过折纸的方法在AD边上找一个点E,使得BE平分∠AEC.(答题要求:简单叙述折纸的方法即可,不需要证明.)

图3
24. 如图1是一块内置量角器的等腰直角三角板,它是一个轴对称图形.已知量角器所在的半圆O的直径DE与AB之间的距离为1,DE=4,AB=8,点N为半圆O上的一个动点,连结AN交半圆或直径DE于点M.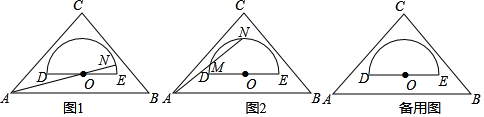 (1)、当AN经过圆心O时,求AN的长;(2)、如图2,若N为量角器上表示刻度为90°的点,求△MON的周长;(3)、当 时,求△MON的面积.
(1)、当AN经过圆心O时,求AN的长;(2)、如图2,若N为量角器上表示刻度为90°的点,求△MON的周长;(3)、当 时,求△MON的面积.