浙教版数学九上第3章 圆的基本性质优生综合题特训
试卷更新日期:2021-11-13 类型:复习试卷
一、综合题
-
1. 如图,在等腰 中, , ,垂足为D,点E为 边上一点,连接 并延长至F,使 ,以 为底边作等腰 .
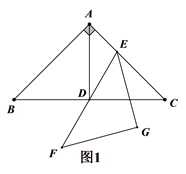
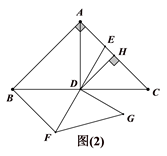
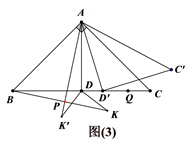 (1)、如图1,若 , ,求 的长;(2)、如图2,连接 , ,点M为 的中点,连接 ,过D作 ,垂足为H,连接 交 于点N,求证: ;(3)、如图3,点K为平面内不与点D重合的任意一点,连接 ,将 绕点D顺时针旋转 得到 ,连接 , ,直线 与直线 交于点P, 为直线 上一动点,连接 并在 的右侧作 且 ,连接 ,Q为 边上一点, , ,当 取到最小值时,直线 与直线 交于点S,请直接写出 的面积.2. 如图,抛物线 与直线 交于 , 两点,直线 : 交 轴于点 .点 是直线 上的动点,过点 作 轴交 于点 ,交抛物线于点 .
(1)、如图1,若 , ,求 的长;(2)、如图2,连接 , ,点M为 的中点,连接 ,过D作 ,垂足为H,连接 交 于点N,求证: ;(3)、如图3,点K为平面内不与点D重合的任意一点,连接 ,将 绕点D顺时针旋转 得到 ,连接 , ,直线 与直线 交于点P, 为直线 上一动点,连接 并在 的右侧作 且 ,连接 ,Q为 边上一点, , ,当 取到最小值时,直线 与直线 交于点S,请直接写出 的面积.2. 如图,抛物线 与直线 交于 , 两点,直线 : 交 轴于点 .点 是直线 上的动点,过点 作 轴交 于点 ,交抛物线于点 . (1)、求抛物线 的表达式.(2)、连接 , ,当四边形 是平行四边形时,求点 的坐标.(3)、①在 轴上存在一点 ,连接 , ,当点 运动到什么位置时,以 , , , 为顶点的四边形是矩形?求出此时点 , 的坐标.
(1)、求抛物线 的表达式.(2)、连接 , ,当四边形 是平行四边形时,求点 的坐标.(3)、①在 轴上存在一点 ,连接 , ,当点 运动到什么位置时,以 , , , 为顶点的四边形是矩形?求出此时点 , 的坐标.②在①的前提下,以点 为圆心, 长为半径作圆,点 为 上一动点,求 的最大值.
3. 在 中, , ,点 在边 上, ,将线段 绕点 顺时针旋转至 ,记旋转角为 ,连接 , ,以 为斜边在其一侧制作等腰直角三角形 .连接 .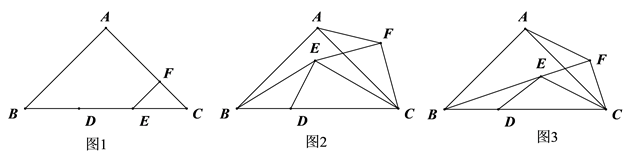 (1)、如图1,当 时,请直接写出线段 与线段 的数量关系;(2)、当 时,
(1)、如图1,当 时,请直接写出线段 与线段 的数量关系;(2)、当 时,①如图2,(1)中线段 与线段 的数量关系是否仍然成立?请说明理由;
②如图3,当 , , 三点共线时,连接 ,判断四边形 的形状,并说明理由.
4. 数学兴趣小组活动中,小明进行数学探究活动,将边长为 的正方形 与边长为 的正方形 按图1位置放置, 与 在同一条直线上, 与 在同一条直线上.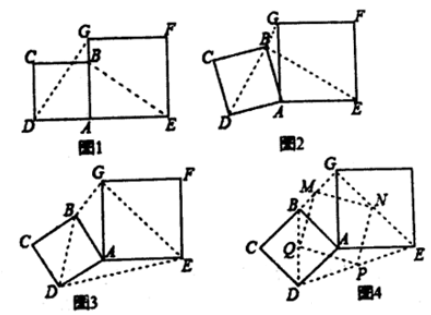 (1)、小明发现 ,请你帮他说明理由.(2)、如图2,小明将正方形 绕点 逆时针旋转,当点 恰好落在线段 上时,请你帮他求出此时 的长.(3)、填空:
(1)、小明发现 ,请你帮他说明理由.(2)、如图2,小明将正方形 绕点 逆时针旋转,当点 恰好落在线段 上时,请你帮他求出此时 的长.(3)、填空:①在旋转过程中,如图3,连接 , , , ,则四边形 的面积最大值为 .
②如图4,分别取 , , , 的中点 , , , ,连接 , , , ,则四边形 的形状为 .
5. 数学课上,有这样一道探究题.如图,已知 中,AB=AC=m,BC=n, ,点P为平面内不与点A、C重合的任意一点,将线段CP绕点P顺时针旋转a,得线段PD,E、F分别是CB、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究 的值和 的度数与m、n、α的关系,请你参与学习小组的探究过程,并完成以下任务:
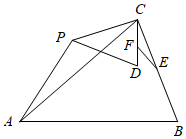 (1)、问题发现:
(1)、问题发现:小明研究了 时,如图1,求出了 , ;
小红研究了 时,如图2,求出了 , ;
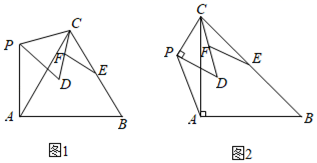 (2)、类比探究:
(2)、类比探究:他们又共同研究了α=120°时,如图3,也求出了 ;
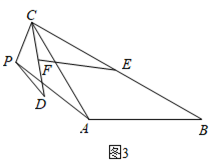
归纳总结:
最后他们终于共同探究得出规律:
(用含m、n的式子表示); (用含α的式子表示).
(3)、求出 时 的值和 的度数.6. 如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形边CB、CD上,连接AF , 取AF中点M , EF的中点N , 连接MD、MN .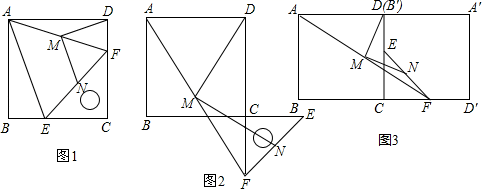 (1)、连接AE , 则△AEF是三角形,MD、MN的数量关系是 .(2)、如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则MD、MN的数量关系还成立吗?若成立,请加以证明;若不成立,请说明理由.(3)、将图1中正方形ABCD及直角三角板ECF同时绕点C顺时针旋转90°,如图3,其他条件不变,则MD、MN的数量关系还成立吗?若成立,请加以证明;若不成立,请说明理由.7. 如图, 为 的外接圆, 为 的直径,点D为 的中点.
(1)、连接AE , 则△AEF是三角形,MD、MN的数量关系是 .(2)、如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则MD、MN的数量关系还成立吗?若成立,请加以证明;若不成立,请说明理由.(3)、将图1中正方形ABCD及直角三角板ECF同时绕点C顺时针旋转90°,如图3,其他条件不变,则MD、MN的数量关系还成立吗?若成立,请加以证明;若不成立,请说明理由.7. 如图, 为 的外接圆, 为 的直径,点D为 的中点.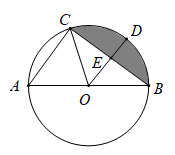 (1)、连接 .求证: .(2)、设 交 于E,若 , .求阴影部分面积.8. 如图
(1)、连接 .求证: .(2)、设 交 于E,若 , .求阴影部分面积.8. 如图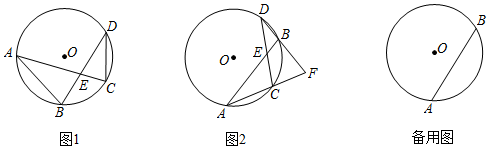 (1)、如图1,在半径为1的 中,弦 , ,且 、 交于点 ,则 .(2)、如图2,在半径为2的 中, ,点 是弧 上任意一点,且 , 与 交于点 ,延长 、 交于点 .
(1)、如图1,在半径为1的 中,弦 , ,且 、 交于点 ,则 .(2)、如图2,在半径为2的 中, ,点 是弧 上任意一点,且 , 与 交于点 ,延长 、 交于点 .①若点 是 的中点,求 的度数.
②若点 不是 的中点, 的度数是否变化?如果变化,请说明理由;如果不变化,请求出 的度数.
9. 如图,在 中,AC为 的直径, AB为 的弦,点 E 是 的中点,过点 E 作 AB 的垂线,交 AB 于点 M ,交 于点 N ,分别连接 EB , CN .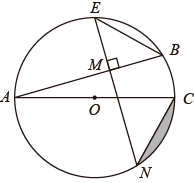 (1)、 与 的数量关系是;(2)、求证: ;(3)、若 , ,求阴影部分图形的面积.10. 如图,在⊙ 中, 是直径, ,垂足为P,过点 的 的切线与 的延长线交于点 , 连接 .
(1)、 与 的数量关系是;(2)、求证: ;(3)、若 , ,求阴影部分图形的面积.10. 如图,在⊙ 中, 是直径, ,垂足为P,过点 的 的切线与 的延长线交于点 , 连接 .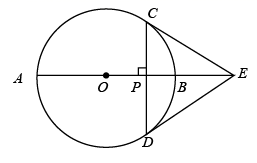 (1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .11. 如图,在 中, ,以 为直径的 交 边于点 , 为 中点,连接 .
(1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .11. 如图,在 中, ,以 为直径的 交 边于点 , 为 中点,连接 .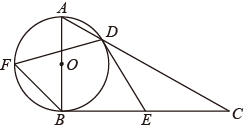 (1)、求证: 与 相切;(2)、 为 的中点,连接 , ,若 , ,求劣弧 的长.12. 如图,AB是⊙O的直径,AC是⊙O的一条弦,点P是⊙O上一点,且PA=PC,PD∥AC,与BA的延长线交于点D.
(1)、求证: 与 相切;(2)、 为 的中点,连接 , ,若 , ,求劣弧 的长.12. 如图,AB是⊙O的直径,AC是⊙O的一条弦,点P是⊙O上一点,且PA=PC,PD∥AC,与BA的延长线交于点D. (1)、求证:PD是⊙O的切线.(2)、若tan∠PBA= ,AC=12,求直径AB的长.13. 已知,⊙O过矩形ABCD的顶点D,且与AB相切于点E,⊙O分别交BC,CD于H,F,G三点.
(1)、求证:PD是⊙O的切线.(2)、若tan∠PBA= ,AC=12,求直径AB的长.13. 已知,⊙O过矩形ABCD的顶点D,且与AB相切于点E,⊙O分别交BC,CD于H,F,G三点.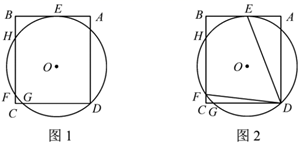 (1)、如图1,求证:BE-AE=CG;(2)、如图2,连接DF,DE.若AE=3,AD=9,tan∠EDF= ,求FC的值.14. 如图, 为半圆 的直径, 为切线, 交半圆 于点 , 为 上一点,且 ,BE的延长线交 于点 ,连结 .
(1)、如图1,求证:BE-AE=CG;(2)、如图2,连接DF,DE.若AE=3,AD=9,tan∠EDF= ,求FC的值.14. 如图, 为半圆 的直径, 为切线, 交半圆 于点 , 为 上一点,且 ,BE的延长线交 于点 ,连结 .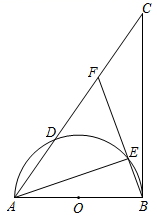 (1)、求证: .(2)、若 , ,求 的长.15. 如图,在 中, , 是边 上一动点,且不与 , 两点重合,连结 ,过点 作 交边 于点 , 的外接圆交边 于另一点 ,连结 .
(1)、求证: .(2)、若 , ,求 的长.15. 如图,在 中, , 是边 上一动点,且不与 , 两点重合,连结 ,过点 作 交边 于点 , 的外接圆交边 于另一点 ,连结 .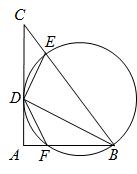 (1)、求证: .(2)、当 , 时.
(1)、求证: .(2)、当 , 时.①若 ,求 的长.
②当线段 , , 中有两条相等时,求出所有符合条件的 的值.
(3)、若 平分 , , ,则 .16. 如图,BC是⊙O的直径,AD是⊙O的弦,AD交BC于点E,连接AB,CD,过点E作EF⊥AB,垂足为F,∠AEF=∠D.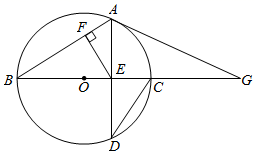 (1)、求证:AD⊥BC;(2)、点G在BC的延长线上,连接AG,∠DAG=2∠D.
(1)、求证:AD⊥BC;(2)、点G在BC的延长线上,连接AG,∠DAG=2∠D.①求证:AG与⊙O相切;
②当 ,CE=4时,直接写出CG的长.
17. 如图,⊙O 的半径为 1,弦AB= ,弦AC , BD 交于点E , 且EA=EB , F是 的中点.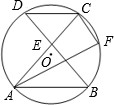 (1)、求证:△CDE 是等腰三角形.(2)、若∠B=50°,求∠F 的度数.(3)、若CF∥BD , 求证:CD=CF ,18. 在平面直角坐标系中,抛物线C1: (m为常数)的顶点为M,与y轴交于点N.(1)、若点P( ,a)在抛物线C1上,求a的值;(2)、当点M到x轴的距离是 时,求m的值;(3)、在(2)的条件下,且m取有理数时,将抛物线C1绕点M旋转180°得到抛物线C2 , 设C2与x轴交于A、B两点(点A在点B的左侧),问在抛物线C2的对称轴上是否存在点Q,使∠AQB=∠ANB?若存在,求点Q的坐标,若不存在,请说明理由.19. 定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做“青竹三角形”.如图1,在△ 和 中,若 ,且 ,则△ 和 是“青竹三角形”.
(1)、求证:△CDE 是等腰三角形.(2)、若∠B=50°,求∠F 的度数.(3)、若CF∥BD , 求证:CD=CF ,18. 在平面直角坐标系中,抛物线C1: (m为常数)的顶点为M,与y轴交于点N.(1)、若点P( ,a)在抛物线C1上,求a的值;(2)、当点M到x轴的距离是 时,求m的值;(3)、在(2)的条件下,且m取有理数时,将抛物线C1绕点M旋转180°得到抛物线C2 , 设C2与x轴交于A、B两点(点A在点B的左侧),问在抛物线C2的对称轴上是否存在点Q,使∠AQB=∠ANB?若存在,求点Q的坐标,若不存在,请说明理由.19. 定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做“青竹三角形”.如图1,在△ 和 中,若 ,且 ,则△ 和 是“青竹三角形”.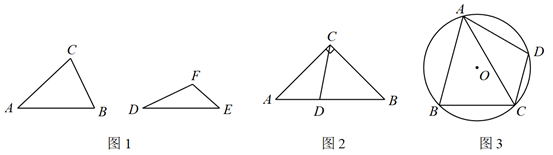 (1)、以下四边形中,一定能被一条对角线分成两个“青竹三角形”的是;(填序号)
(1)、以下四边形中,一定能被一条对角线分成两个“青竹三角形”的是;(填序号)①平行四边形;②矩形;③菱形;④正方形.
(2)、如图2,△ , , ,点D是 上任意一点(不与点A、B重合),设AD、BD、CD的长分别为a、b、c,请写出图中的一对“青竹三角形”,并用含a、b的式子来表示 ;(3)、如图3,⊙O的半径为4,四边形ABCD是⊙O的内接四边形,且△ABC和△ADC是“青竹三角形”.①求 的值;
②若 , ,求△ABC和△ADC的周长之差.
20. 如图,四边形 是⊙ 的内接矩形,过点 的切线与 的延长线交于点 ,连接 与 交于点 , , . (1)、求证: ;(2)、设 ,求 的面积(用 的式子表示);(3)、若 ,求 的长.21. 如图1,四边形 内接于 , 为直径,过点 作 于点 ,连接 .
(1)、求证: ;(2)、设 ,求 的面积(用 的式子表示);(3)、若 ,求 的长.21. 如图1,四边形 内接于 , 为直径,过点 作 于点 ,连接 .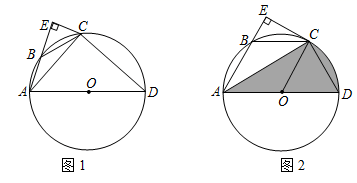 (1)、求证: ;(2)、若 是 的切线, ,连接 ,如图2.
(1)、求证: ;(2)、若 是 的切线, ,连接 ,如图2.①请判断四边形ABCO的形状,并说明理由;
②当AB=2时,求AD , AC与 围成阴影部分的面积.
22. 小明对教材“课题学习”中的“用一张正方形折出一个正八边形”的问题进行了认真的探索。他先把正方形ABCD沿对角线AC对折,再把∠BAC对折,使点B落在AC上,记为点E,然后沿CE的中垂线折叠,得到折痕PQ,如图1,类似地,折出其余三条折痕GH,IJ,KO,得到八边形GHIJKOPQ,如图2。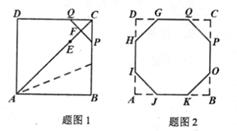 (1)、求证:△CPQ是等腰直角三角形。(2)、若AB=a,求PQ的长。(用含a的代数式表示)(3)、我们把八条边长相等,八个内角都相等的八边形叫做正八边形.试说明八边形GHIJKOPQ是正八边形,请把过程补充完整。
(1)、求证:△CPQ是等腰直角三角形。(2)、若AB=a,求PQ的长。(用含a的代数式表示)(3)、我们把八条边长相等,八个内角都相等的八边形叫做正八边形.试说明八边形GHIJKOPQ是正八边形,请把过程补充完整。解:理由如下:
①

∴∠GQP=135°
同理可得:∠QPO=∠POK=∠OKJ=∠KJI=∠JIH=∠IHG=∠HGQ=135°。
②

∴PQ=QG。
同理可得:QG=GH=HI=IJ=JK=KO=PO=PQ
∴八边形GHIJKOPQ是正八边形。
23. 如图,四边形ABCD中,∠B=∠C=90°,点E为BC中点,AE⊥DE于点E.点O是线段AE上的点,以点O为圆心,OE为半径的⊙O与AB相切于点G,交BC于点F,连接OG.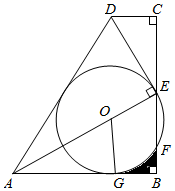 (1)、求证:△ECD∽△ABE;(2)、求证:⊙O与AD相切;(3)、若BC=6,AB=3 ,求⊙O的半径和阴影部分的面积.24. 如图,已知圆O是正六边形ABCDEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x , EH=y .
(1)、求证:△ECD∽△ABE;(2)、求证:⊙O与AD相切;(3)、若BC=6,AB=3 ,求⊙O的半径和阴影部分的面积.24. 如图,已知圆O是正六边形ABCDEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x , EH=y .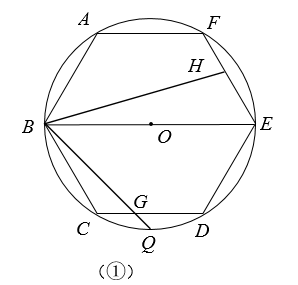
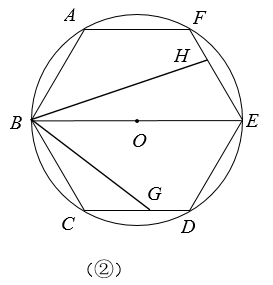
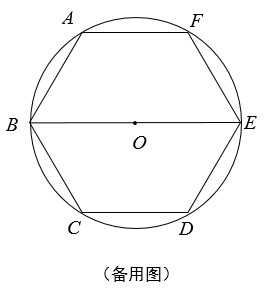 (1)、如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;(2)、如图②,当点G在边CD上时,试写出y关于x的函数关系式,
(1)、如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;(2)、如图②,当点G在边CD上时,试写出y关于x的函数关系式,并写出x的取值范围;
(3)、联结AH、EG , 如果△AFH与△DEG相似,求CG的长.