浙江省湖州市长兴县2021-2022学年九年级上学期数学月考试卷(一)
试卷更新日期:2021-11-12 类型:月考试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 二次函数y=2x2的图象一定过点( )A、(1,﹣2) B、(﹣1,﹣2) C、(﹣1,2) D、(1,0)2. 下列成语或词语所反映的事件中,发生的可能性最小的是( )A、瓜熟蒂落 B、守株待兔 C、旭日东升 D、瓮中捉鳖3. 二次函数y=x2﹣2x+4图象的顶点坐标是( )A、(1,3) B、(1,﹣3) C、(﹣1,3) D、(﹣1,﹣3)4. 二次函数y=(x+2)2﹣1的图象大致为( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )
5. 如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )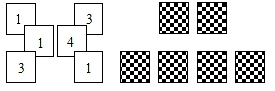 A、 B、 C、 D、6. 小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( )
A、 B、 C、 D、6. 小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( ) A、4.4 B、3.4 C、2.4 D、1.47. 已知(﹣3,y1),(﹣2,y2),(1,y3)是抛物线y=﹣3x2﹣12x+m上的点,则对y1 , y2和y3的大小关系判断正确的是( )A、y3<y2<y1 B、y3<y1<y2 C、y2<y3<y1 D、y1<y3<y28. 如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A、4.4 B、3.4 C、2.4 D、1.47. 已知(﹣3,y1),(﹣2,y2),(1,y3)是抛物线y=﹣3x2﹣12x+m上的点,则对y1 , y2和y3的大小关系判断正确的是( )A、y3<y2<y1 B、y3<y1<y2 C、y2<y3<y1 D、y1<y3<y28. 如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )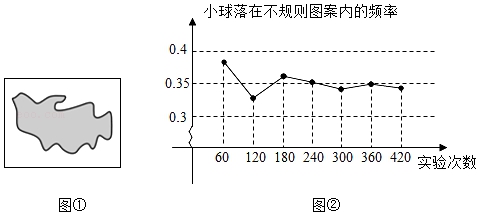 A、6m2 B、7m2 C、8m2 D、9m29. 如图,已知y= 与y=x2﹣7的图象的交点A(﹣2,﹣3),B(﹣1,﹣6),C(3,2),则不等式x2> +7的解集为( )
A、6m2 B、7m2 C、8m2 D、9m29. 如图,已知y= 与y=x2﹣7的图象的交点A(﹣2,﹣3),B(﹣1,﹣6),C(3,2),则不等式x2> +7的解集为( ) A、x<﹣2或x>3 B、﹣2<x<﹣1或0<x<3 C、﹣2<x<﹣1或x>3 D、x<﹣2或﹣1<x<0或x>310. 学校卫生间的洗手盘台面上有一瓶洗手液(如图①).小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是( )
A、x<﹣2或x>3 B、﹣2<x<﹣1或0<x<3 C、﹣2<x<﹣1或x>3 D、x<﹣2或﹣1<x<0或x>310. 学校卫生间的洗手盘台面上有一瓶洗手液(如图①).小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是( )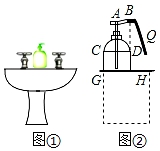 A、﹣ B、 C、﹣ D、
A、﹣ B、 C、﹣ D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 二次函数y=ax2﹣2x+1的图象与y轴的交点坐标是 .12. 将二次函数y=x2的图象平移后经过点(2,0),则平移后所得图象对应的函数解析式可能是.(写出一个符合要求的答案即可)13. 有的同学认为:抛掷两枚均匀硬币,硬币落地后,朝上一面只可能有以下三种情况:
⑴全是正面;⑵一正一反;⑶全是反面.
出现一正一反的概率是.
14. 二次函数y=ax2+bx+c的部分对应值如下表:x
…
﹣3
﹣2
0
1
3
5
…
y
…
7
0
﹣8
﹣9
﹣5
7
…
则当x=2时对应的函数值y= .
15. 如图,在平面直角坐标系xOy中,正方形OABC的顶点B在第一象限内,A,C分别在x轴和y轴上,抛物线y= (x﹣a)2+b经过B,C两点,顶点D在正方形OABC内部.若点D在直线y=x+2上,则a+b的值是. 16. 某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y= x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为元.
16. 某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y= x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为元.三、解答题(本题有8小题,共66分)
-
17. 用配方法把二次函数y= x2﹣4x+5化为y=a(x﹣m)2+k的形式,并写出该函数图象的顶点坐标.18. 某路口南北方向红绿灯的设置时间为:红灯40s、绿灯60s、黄灯3s.司机A随机地由南往北开车到达该路口,问:(1)、他遇到红灯的概率大还是遇到绿灯的概率大?(2)、他遇到绿灯的概率是多少?19. 已知抛物线y=ax2+bx+1经过点(1,﹣2),(﹣2,13).(1)、求a,b的值;(2)、若(5,n),(m,n)是抛物线上不同的两点,求m的值.20. 一只不透明袋子中装有1个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
摸球的次数
200
300
400
1000
1600
2000
摸到白球的频数
72
93
130
334
532
667
摸到白球的频率
0.3600
0.3100
0.3250
0.3340
0.3325
0.3335
(1)、该学习小组发现,摸到白球的频率在一个常数附近摆动,这个常数是 . (精确到0.01),由此估出红球有个.(2)、现从该袋中一次摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球,1个红球的概率.21. 如图,已知抛物线经过点A(﹣1,0),B(3,0),与y轴交于点C,顶点D的纵坐标为4. (1)、求抛物线的函数表达式.(2)、连结BC,CD,BD,请判断△BCD的形状,并说明理由.22. 某植物园有一块足够大的空地,其中有一堵长为6米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图所示的两种方案:
(1)、求抛物线的函数表达式.(2)、连结BC,CD,BD,请判断△BCD的形状,并说明理由.22. 某植物园有一块足够大的空地,其中有一堵长为6米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图所示的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)、若按方案甲施工,且围成面积为25平方米的花圃,则AD的长是多少米?(2)、按哪种方案施工,可以围成的矩形花圃的面积最大?最大面积是多少?23. 如图1,地面OB上两根等长立柱AO,CB之间悬挂一根近似成抛物线y= x2﹣ x+3的绳子.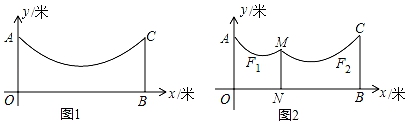 (1)、求绳子最低点离地面的距离;(2)、因实际需要,在离AO为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;(3)、保持(2)中点N的位置不变,将立柱MN的长度提升为3米,发现抛物线F1和F2的形状和大小都一样,测得抛物线F1和F2的最低点到地面的高度相差0.5米,求抛物线F1对应函数的二次项系数.24. 如图,在平面直角坐标系xOy中,已知抛物线y=﹣ (x﹣m)2+4的顶点为A,与y轴的交点B,异于点A的点C(1,n)在该抛物线上,直线AC与y轴和x轴分别交于点D,E.
(1)、求绳子最低点离地面的距离;(2)、因实际需要,在离AO为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;(3)、保持(2)中点N的位置不变,将立柱MN的长度提升为3米,发现抛物线F1和F2的形状和大小都一样,测得抛物线F1和F2的最低点到地面的高度相差0.5米,求抛物线F1对应函数的二次项系数.24. 如图,在平面直角坐标系xOy中,已知抛物线y=﹣ (x﹣m)2+4的顶点为A,与y轴的交点B,异于点A的点C(1,n)在该抛物线上,直线AC与y轴和x轴分别交于点D,E. (1)、当m=﹣3时,求n的值;(2)、若点A在第一象限,当∠AEO=45°时,求证:AC=CE;(3)、当在线段OD上时,求m的取值范围.
(1)、当m=﹣3时,求n的值;(2)、若点A在第一象限,当∠AEO=45°时,求证:AC=CE;(3)、当在线段OD上时,求m的取值范围.