贵州省遵义市2021-2022学年七年级上学期数学第一次月考试卷
试卷更新日期:2021-11-12 类型:月考试卷
一、单选题
-
1. 一实验室检测A、B、C、D四个零件的质量(单位∶克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的零件是( )A、
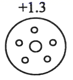 B、
B、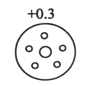 C、
C、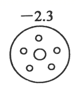 D、
D、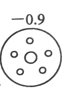 2. 的相反数是( )A、2021 B、-2021 C、 D、3. 2020年1~10月份,全国规模以上工业企业实现营业收入83.78万亿元,其中83.78万亿用科学记数法可表示为( )A、 83.78×1012 B、8.378×1013 C、0.8378×1014 D、8.378×1054. 下列说法正确的是( )A、 表示一个负数 B、正整数和负整数统称整数 C、 表示一个奇数 D、非负数包括零和正数5. 如果 ,那么 的取值范围是( )A、x≤2; B、x≥2; C、x<2; D、x>2;6. 下列各式中正确的是( )A、+5﹣(﹣6)=11 B、﹣7﹣|﹣7|=0 C、﹣5+(+3)=2 D、(﹣2)+(﹣5)=77. 下列说法正确的有( )A、有理数不是负数就是正数 B、任何有理数都有相反数 C、任何有理数都有倒数 D、绝对值等于相反数的数是负数8. 0.2的倒数是( )A、5 B、 C、 D、29. 如图 的正方形方格中共有9个空格,小林同学想在每个空格中分别填入1、2、3三个数字中的一个,使得处于同一横行、同一竖列、同一对角线上的3个数字之和均不相等,你认为小林的设想能实现吗?( )
2. 的相反数是( )A、2021 B、-2021 C、 D、3. 2020年1~10月份,全国规模以上工业企业实现营业收入83.78万亿元,其中83.78万亿用科学记数法可表示为( )A、 83.78×1012 B、8.378×1013 C、0.8378×1014 D、8.378×1054. 下列说法正确的是( )A、 表示一个负数 B、正整数和负整数统称整数 C、 表示一个奇数 D、非负数包括零和正数5. 如果 ,那么 的取值范围是( )A、x≤2; B、x≥2; C、x<2; D、x>2;6. 下列各式中正确的是( )A、+5﹣(﹣6)=11 B、﹣7﹣|﹣7|=0 C、﹣5+(+3)=2 D、(﹣2)+(﹣5)=77. 下列说法正确的有( )A、有理数不是负数就是正数 B、任何有理数都有相反数 C、任何有理数都有倒数 D、绝对值等于相反数的数是负数8. 0.2的倒数是( )A、5 B、 C、 D、29. 如图 的正方形方格中共有9个空格,小林同学想在每个空格中分别填入1、2、3三个数字中的一个,使得处于同一横行、同一竖列、同一对角线上的3个数字之和均不相等,你认为小林的设想能实现吗?( ) A、一定可以 B、一定不可以 C、有可能 D、无法判断10. 某商店在某一时间以每件100元的价格卖出两件衣服,其中一件盈利25%,另一件亏损20%,则该商店卖出这两件衣服的盈亏情况为( )A、不盈也不亏 B、盈利5元 C、亏损5元 D、盈利10元11. 定义一种对正整数 的“ ”运算:①当 为奇数时,结果为 ;②当 为偶数时,结果为 ;(其中 是使 为奇数的正整数),并且运算可以重复进行,例如取 .则:若n=49,则第449次“F运算”的结果是( )
A、一定可以 B、一定不可以 C、有可能 D、无法判断10. 某商店在某一时间以每件100元的价格卖出两件衣服,其中一件盈利25%,另一件亏损20%,则该商店卖出这两件衣服的盈亏情况为( )A、不盈也不亏 B、盈利5元 C、亏损5元 D、盈利10元11. 定义一种对正整数 的“ ”运算:①当 为奇数时,结果为 ;②当 为偶数时,结果为 ;(其中 是使 为奇数的正整数),并且运算可以重复进行,例如取 .则:若n=49,则第449次“F运算”的结果是( ) A、 B、 C、 D、12. 如果一个正整数可以表示为两个连续奇数的立方差,则称这个正整数为“和谐数”.如:2=13﹣(﹣1)3 , 26=33﹣13 , 2和26均为和谐数.那么,不超过2019的正整数中,所有的“和谐数”之和为( )A、6858 B、6860 C、9260 D、9262
A、 B、 C、 D、12. 如果一个正整数可以表示为两个连续奇数的立方差,则称这个正整数为“和谐数”.如:2=13﹣(﹣1)3 , 26=33﹣13 , 2和26均为和谐数.那么,不超过2019的正整数中,所有的“和谐数”之和为( )A、6858 B、6860 C、9260 D、9262二、填空题
-
13. 计算:|-7+3|=.14. 温度由 ℃上升 ℃,达到的温度是℃.15. 若a,b互为相反数,c,d互为倒数,则2021(a+b)-2020cd=.16. 规定图形
 表示运算 ,图形
表示运算 ,图形  表示运算 .则
表示运算 .则  +
+  =(直接写出答案). 17. 把下列各数填在相应的大括号内:﹣5,|﹣ |,﹣12,0,﹣3.14,+1.99,﹣(﹣6), ,200%,15%.(1)、正数集合:{ …};(2)、负数集合:{ …};(3)、整数集合:{ …};(4)、分数集合:{ …}.
=(直接写出答案). 17. 把下列各数填在相应的大括号内:﹣5,|﹣ |,﹣12,0,﹣3.14,+1.99,﹣(﹣6), ,200%,15%.(1)、正数集合:{ …};(2)、负数集合:{ …};(3)、整数集合:{ …};(4)、分数集合:{ …}.三、解答题
-
18. 计算:(1)、
 ; (2)、 .
; (2)、 .
19. ﹣4,5,﹣7三数的和比这三数的绝对值的和小多少?
20. 有理数a、b、c在数轴上的位置如图: (1)、判断正负,用“>”或“<”填空:b﹣c0,b﹣a0,c﹣a0.(2)、化简:|b﹣c|+|b﹣a|﹣|c﹣a|.21. 阅读下面的解题过程:
(1)、判断正负,用“>”或“<”填空:b﹣c0,b﹣a0,c﹣a0.(2)、化简:|b﹣c|+|b﹣a|﹣|c﹣a|.21. 阅读下面的解题过程:计算:(-15)÷ ×6.
解:原式=(-15)÷ ×6(第一步)
=(-15)÷(-1)(第二步)
=-15.(第三步)
回答:
(1)、上面解题过程中有两处错误,第一处是第步,错误的原因是;第二处是第 , 错误的原因是.(2)、把正确的解题过程写出来.22. 对于一个数x,我们用 表示小于x的最大整数,例如: , .(1)、填空: , , ;(2)、若a,b都是整数,且 和 互为相反数,求代数式 的值;(3)、若 ,求x的取值范围.23. 某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况(超产记为正、减产记为负):星期
一
二
三
四
五
六
日
增减(单位:个)
+5
﹣2
﹣5
+15
﹣10
+16
﹣9
(1)、写出该厂星期一生产工艺品的数量;(2)、写出本周产量最多的一天比最少的一天多生产多少个工艺品?(3)、请求出该工艺厂在本周实际生产工艺品的数量;(4)、已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.24. 如图,有两条线段,AB=2(单位长度),CD=1(单位长度)在数轴上,点A在数轴上表示的数是﹣12,点D在数轴上表示的数是15. (1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长=;(2)、若线段AB以1个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.当点B与C重合时,点B与点C在数轴上表示的数是多少?(3)、若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度/秒的速度也向左匀速运动.设运动时间为t秒,当0<t<24时,M为AC中点,N为BD中点,则线段MN的长为多少?
(1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长=;(2)、若线段AB以1个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.当点B与C重合时,点B与点C在数轴上表示的数是多少?(3)、若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度/秒的速度也向左匀速运动.设运动时间为t秒,当0<t<24时,M为AC中点,N为BD中点,则线段MN的长为多少?