江西省南昌市安义县2021-2022学年九年级上学期10月月考数学试题
试卷更新日期:2021-11-12 类型:月考试卷
一、单选题
-
1. 把方程 化为一般形式后二次项系数为1,则一次项系数与常数项的和是( ).A、5 B、-1 C、1 D、-52. 下列二次函数中,其图象的顶点坐标是 的是( ).A、 B、 C、 D、3. 若关于x的一元二次方程 的一个根是3,则 的值是( ).A、-2 B、2 C、-3 D、34. 在解方程 时,对方程进行配方,文本框①中是小贤做的,文本框②中是小淇做的,对于两人的做法,下列说法正确的是( ).
,
,
,
.
①
,
,
,
.
②
A、两人都正确 B、小贤正确,小淇错误 C、小贤错误,小淇正确 D、两人都错误5. 根据图中的程序,当输入一元二次方程 的根x时,输出结果y的值为( ). A、-4或-1 B、-4 C、2 D、-4或16. 在同一平面直角坐标系中,函数 和函数 (m是常数,且 )的图象可能是( ).A、
A、-4或-1 B、-4 C、2 D、-4或16. 在同一平面直角坐标系中,函数 和函数 (m是常数,且 )的图象可能是( ).A、 B、
B、 C、
C、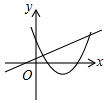 D、
D、
二、填空题
-
7. 方程 的解是 .8. 将二次函数 的图象向上平移1个单位长度,所得图象的解析式是 .9. 在2021年10月的日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为180,则这个最小数为 .
 10. 若一元二次方程 的两根为 , ,则 的值为 .11. 如图所示的是-一个长为60m,宽为40m的矩形花园,现要在花园中修建等宽(宽度为x m)的小道,剩余的地方种植花草.要使种植花草的面积为 ,则可列方程为 .
10. 若一元二次方程 的两根为 , ,则 的值为 .11. 如图所示的是-一个长为60m,宽为40m的矩形花园,现要在花园中修建等宽(宽度为x m)的小道,剩余的地方种植花草.要使种植花草的面积为 ,则可列方程为 . 12. 在平面直角坐标系xOy中,函数 (其中 )的图象记为W,图象W经过点 ,则n的值为 .
12. 在平面直角坐标系xOy中,函数 (其中 )的图象记为W,图象W经过点 ,则n的值为 .三、解答题
-
13. 用适当的方法解下列方程:(1)、 .(2)、已知二次函数的图象以 为顶点且过点 ,求该函数的解析式.14. 已知:关于x的方程 .(1)、试说明无论k取何值时,方程总有两个不相等的实数根:(2)、若 ,请解此方程.15. 如图,在平面直角坐标系中,矩形OABC的顶点C,A分别在x轴,y轴上,经过A,C两点的抛物线交x轴于另一点D,连接AC.请仅用无刻度的直尺完成以下作图.(保留作图痕迹)
 (1)、在图1中的抛物线上找出点E,使 .(2)、在图2中的抛物线上作出该抛物线的顶点F.16. 如图所示的是某个二次函数的图象.
(1)、在图1中的抛物线上找出点E,使 .(2)、在图2中的抛物线上作出该抛物线的顶点F.16. 如图所示的是某个二次函数的图象.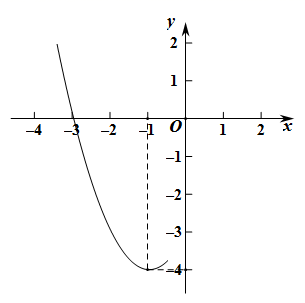 (1)、求该二次函数的解析式.(2)、补全函数图象.17. 已知二次函数y=x2+bx+c的函数值y与自变量x之间的对应数据如表:
(1)、求该二次函数的解析式.(2)、补全函数图象.17. 已知二次函数y=x2+bx+c的函数值y与自变量x之间的对应数据如表:x
…
﹣1
0
1
2
3
4
…
y
…
10
5
2
1
2
5
…
(1)、求b、c的值;(2)、当x取何值时,该二次函数有最小值,最小值是多少?18. 解方程 时,我们将 作为一个整体,设 ,则原方程化为 .解得 .当 时, ,解得 或 .当 时, ,解得 或 .所以,原方程的解为 .模仿材料中解方程的方法,求方程 的解.
19. 2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,传承红色基因”主题教育学习活动,井冈山是此次活动重要的研学活动基地.据了解,今年7月份该基地接待参观人数100万,9月份接待参观人数增加到121万.(1)、求这两个月参观人数的月平均增长率.(2)、按照这个增长率,预计10月份的参观人数是多少?20. 如图,已知抛物线y=x2-(k+1)x+1的顶点A在x轴的负半轴上,且与一次函数y=-x+1交于点B和点C (1)、求k的值;(2)、求 ABC的面积.21. 设二次函数 , 的图象的顶点坐标分别为 , .若 , ,且开口方向相同,则称 是 的“反倍顶二次函数”.(1)、请写出二次函数 的一个“反倍顶二次函数”.(2)、已知关于x的二次函数 和二次函数 .若函数 恰是 的“反倍顶二次函数”,求n的值.22. 在解一元二次方程时,发现有这样一种解法:
(1)、求k的值;(2)、求 ABC的面积.21. 设二次函数 , 的图象的顶点坐标分别为 , .若 , ,且开口方向相同,则称 是 的“反倍顶二次函数”.(1)、请写出二次函数 的一个“反倍顶二次函数”.(2)、已知关于x的二次函数 和二次函数 .若函数 恰是 的“反倍顶二次函数”,求n的值.22. 在解一元二次方程时,发现有这样一种解法:如:解方程 .
解:原方程可变形,得 ,
,
,
直接开平方,得 , .
我们称这种解法为“平均数法”
(1)、下面是小明用“平均数法”解方程 时写的解题过程:解:原方程可变形,得 ,
,
,
直接开平方,得 , .
上述解题过程中的a,b,c,d所表示的数分别是 , , , .
(2)、请用“平均数法”解方程: .23. 如图,函数y=-x2+ x+c(-2020≤x≤1)的图象记为L1 , 最大值为M1;函数y=-x2+2cx+1(1≤x≤2020)的图象记为L2 , 最大值为M2 . L1的右端点为A,L2的左端点为B,L1 , L2合起来的图形记为L. (1)、当c=1时,求M1 , M2的值;(2)、若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;(3)、若M1 , M2的差为 ,直接写出c的值.
(1)、当c=1时,求M1 , M2的值;(2)、若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;(3)、若M1 , M2的差为 ,直接写出c的值.