内蒙古自治区赤峰市松山区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2021-11-12 类型:期末考试
一、单选题
-
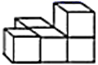
1. =( )A、 B、 C、 D、2. 我国的领水面积约为370000 ,用科学记数法表示370000这个数为( )A、37× B、3.7× C、0.37× D、3.7×3. 由5个小立方体搭成如图所示的几何体,从正面看到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列方程为一元一次方程的是( )A、y+3=0 B、x+2y=3 C、x2=2x D、+y=25. 下列说法错误的是( )A、5y4是四次单项式 B、5是单项式 C、 的系数是 D、3a2+2a2b﹣4b2是二次三项式6. 如图,数轴上点M表示的数可能是( )
4. 下列方程为一元一次方程的是( )A、y+3=0 B、x+2y=3 C、x2=2x D、+y=25. 下列说法错误的是( )A、5y4是四次单项式 B、5是单项式 C、 的系数是 D、3a2+2a2b﹣4b2是二次三项式6. 如图,数轴上点M表示的数可能是( )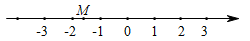 A、1.5 B、-2.6 C、-1.6 D、2.67. 下面合并同类项正确的是( )A、3x+2x2=5x3 B、2a2b﹣a2b=1 C、﹣ab﹣ab=0 D、﹣y2x+xy2=08. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β均为锐角且相等的是( )A、
A、1.5 B、-2.6 C、-1.6 D、2.67. 下面合并同类项正确的是( )A、3x+2x2=5x3 B、2a2b﹣a2b=1 C、﹣ab﹣ab=0 D、﹣y2x+xy2=08. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β均为锐角且相等的是( )A、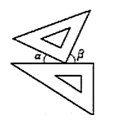 B、
B、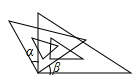 C、
C、 D、
D、 9. 如果∠α=52°25′,则∠α的余角的度数为( )A、38°25′ B、37°45′ C、37°35′ D、127°35′10. 下面图形中,射线 是表示北偏东60°方向的是( )A、
9. 如果∠α=52°25′,则∠α的余角的度数为( )A、38°25′ B、37°45′ C、37°35′ D、127°35′10. 下面图形中,射线 是表示北偏东60°方向的是( )A、 B、
B、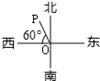 C、
C、 D、
D、 11. 郝炜同学在计算35+x时,误将“+”看成“﹣”,结果得10,则35+x的值应为( )A、20 B、60 C、10 D、7012. 某商店换季促销,将一件标价为240元的T恤8折售出,获利20%,则这件T恤的成本为( )A、144元 B、160元 C、192元 D、200元13. 北流市某风景区的门票价格在2019年国庆期间有如下优惠:购票人数为1~50人时,每人票价格为50元;购票人数为51~100人时,每人门票价格45元;购票人数为100人以上时,每人门票价格为40元.某初中初一有两班共103人去该风景区,如果两班都以班为单位分别购票,一共需付 4860元,则两班人数分别为( )A、56,47 B、57,48 C、58,45 D、59,4414. 下面两个多位数1248624…,6248624…,都是按照如下方法得到的:从首位数字开始,将左边数字乘以2,若积为一位数,将其写在右边数位上,若积为两位数,则将其个位数字写在右边数位上.依次再进行如上操作得到第3位数字…后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,按如上操作得到一个多位数,则这个多位数前2020位的所有数字之和是( )A、10091 B、10095 C、10099 D、10107
11. 郝炜同学在计算35+x时,误将“+”看成“﹣”,结果得10,则35+x的值应为( )A、20 B、60 C、10 D、7012. 某商店换季促销,将一件标价为240元的T恤8折售出,获利20%,则这件T恤的成本为( )A、144元 B、160元 C、192元 D、200元13. 北流市某风景区的门票价格在2019年国庆期间有如下优惠:购票人数为1~50人时,每人票价格为50元;购票人数为51~100人时,每人门票价格45元;购票人数为100人以上时,每人门票价格为40元.某初中初一有两班共103人去该风景区,如果两班都以班为单位分别购票,一共需付 4860元,则两班人数分别为( )A、56,47 B、57,48 C、58,45 D、59,4414. 下面两个多位数1248624…,6248624…,都是按照如下方法得到的:从首位数字开始,将左边数字乘以2,若积为一位数,将其写在右边数位上,若积为两位数,则将其个位数字写在右边数位上.依次再进行如上操作得到第3位数字…后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,按如上操作得到一个多位数,则这个多位数前2020位的所有数字之和是( )A、10091 B、10095 C、10099 D、10107二、填空题
-
15. 若一个角的余角是它的2倍,这个角的补角为°.16. 某轮船顺水航行3h,逆水航行 ,已知轮船在静水中的速度是 ,水流速度是 ,则轮船顺水比逆水多航行 .17. 一个多项式加上 得到 ,则这个多项式是 .18. 如图是一个 的正方形格子,要求横、竖、对角线上的三个数之和相等,请根据图中提供的信息求出 等于 .

三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 解方程:(1)、5(x+8)﹣5=6(2x﹣7)(2)、 ﹣x=3﹣21. 如图,线段AC=6cm,线段AB=21cm,M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
 22. 如图所示,是一个长方体纸盒平面展开图,已知纸盒中相对两个面上的数互为相反数.求a,b,c的值?
22. 如图所示,是一个长方体纸盒平面展开图,已知纸盒中相对两个面上的数互为相反数.求a,b,c的值?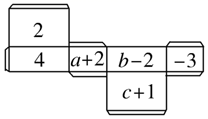 23. 已知甲、乙两地相距160km,A、B两车分别从甲、乙两地同时出发,A车速度为85km/h,B车速度为65km/h.(1)、A、B两车同时同向而行,A车在后,经过几小时A车追上B车?(2)、A、B两车同时相向而行,经过几小时两车相距20km?24. 今年假期某校对操场进行了维修改造,如图是操场的一角.在长为 米,宽为 米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为 米.
23. 已知甲、乙两地相距160km,A、B两车分别从甲、乙两地同时出发,A车速度为85km/h,B车速度为65km/h.(1)、A、B两车同时同向而行,A车在后,经过几小时A车追上B车?(2)、A、B两车同时相向而行,经过几小时两车相距20km?24. 今年假期某校对操场进行了维修改造,如图是操场的一角.在长为 米,宽为 米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为 米. (1)、直接写出一个篮球场的长和宽;(用含字母 , , 的代数式表示)(2)、用含字母 , , 的代数式表示这两个篮球场占地面积的和,并求出当 , , 时,这两个篮球场占地面积的和.25. 某大型商场销售一种茶具和茶碗,茶具每套定价200元,茶碗每只定价20元,“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案,方案一:买一套茶具送一只茶碗;方案二,茶具和茶碗按定价的九五折付款,现在某客户要到商场购买茶具30套,茶碗x只(x>30).(1)、若客户按方案一,需要付款元;若客户按方案二,需要付款元.(用含x的代数式表示)(2)、若x=40,试通过计算说明此时哪种购买方案比较合适?(3)、当x=40,能否找到一种更为省钱的方案,如果能,写出你的方案,并计算出此方案应付钱数;如果不能,说明理由.26. 如图1,点 为直线 上一点,过点 作射线 ,使 将一直角三角板的直角顶点放在点 处,一边 在射线 上,另一边 在直线 的下方.
(1)、直接写出一个篮球场的长和宽;(用含字母 , , 的代数式表示)(2)、用含字母 , , 的代数式表示这两个篮球场占地面积的和,并求出当 , , 时,这两个篮球场占地面积的和.25. 某大型商场销售一种茶具和茶碗,茶具每套定价200元,茶碗每只定价20元,“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案,方案一:买一套茶具送一只茶碗;方案二,茶具和茶碗按定价的九五折付款,现在某客户要到商场购买茶具30套,茶碗x只(x>30).(1)、若客户按方案一,需要付款元;若客户按方案二,需要付款元.(用含x的代数式表示)(2)、若x=40,试通过计算说明此时哪种购买方案比较合适?(3)、当x=40,能否找到一种更为省钱的方案,如果能,写出你的方案,并计算出此方案应付钱数;如果不能,说明理由.26. 如图1,点 为直线 上一点,过点 作射线 ,使 将一直角三角板的直角顶点放在点 处,一边 在射线 上,另一边 在直线 的下方. (1)、将图1中的三角形板绕点 按照顺时针方向旋转至图2的位置,使得 落在射线 上,此时 旋转的角度是°;(2)、继续将图2中的三角板绕点 按顺时针方向旋转至图3的位置,使得 在 的内部,则 °;(3)、在上述直角板从图1旋转到图3的位置的过程中,若三角板绕点 按每秒钟 的速度旋转,当 恰好为 的平分线时,此时,三角板绕点 运动时间为 ▲ 秒,并说明理由.
(1)、将图1中的三角形板绕点 按照顺时针方向旋转至图2的位置,使得 落在射线 上,此时 旋转的角度是°;(2)、继续将图2中的三角板绕点 按顺时针方向旋转至图3的位置,使得 在 的内部,则 °;(3)、在上述直角板从图1旋转到图3的位置的过程中,若三角板绕点 按每秒钟 的速度旋转,当 恰好为 的平分线时,此时,三角板绕点 运动时间为 ▲ 秒,并说明理由.