内蒙古自治区包头市青山区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2021-11-12 类型:期末考试
一、单选题
-
1. 高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做包含的数学道理是( )A、两点确定一条直线 B、两点之间,线段最短 C、两条直线相交,只有一个交点 D、直线是向两个方向无限延伸的2. 2020年新华社日内瓦5月5日电,世卫组织公布中国以外新冠肺炎确诊病例达340多万例,将340万用科学记数法表示应为( )A、 34×106 B、3.4×105 C、0.34×107 D、3.4×1063. 某学习小组将要进行一次统计活动,下面是四位同学分别设计的活动序号,其中正确的是( )A、实际问题→收集数据→表示数据→整理数据→统计分析合理决策 B、实际问题→表示数据→收集数据→整理数据→统计分析合理决策 C、实际问题→收集数据→整理数据→表示数据→统计分析合理决策 D、实际问题→整理数据→收集数据→表示数据→统计分析合理决策4. 下列说法正确的是( )A、 一定是负数 B、 是二次三项式 C、-5不是单项式 D、 的系数是5. 如图,是小明同学在数学实践课上,所设计的正方体盒子的平面展开图,每个面上都有一个汉字,请你判断,正方体盒子上与“善”字相对的面上的字是
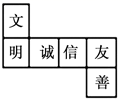 A、文 B、明 C、诚 D、信6. 单项式 与 的和是单项式,则 的值是( )A、 B、 C、 D、7. 下列说法正确的个数为( )
A、文 B、明 C、诚 D、信6. 单项式 与 的和是单项式,则 的值是( )A、 B、 C、 D、7. 下列说法正确的个数为( )①用一个平面去截一个圆锥,截面的形状可能是一个三角形;
②若2AB=AC,则点B是AC的中点;
③连接两点的线段叫做这两点之间的距离;
④在数轴上,点A、B分别表示有理数a、b,若a>b,则A到原点的距离比B到原点的距离大.
A、1个 B、2个 C、3个 D、4个8. 如图是由同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形.请仔细观察图形,则在第 个图中白色瓷砖比黑色瓷砖多( )块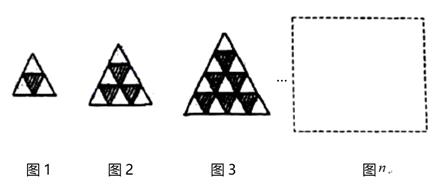 A、 B、 C、 D、9. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A、 B、 C、 D、9. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ) A、点A B、点B C、AB之间 D、BC之间
A、点A B、点B C、AB之间 D、BC之间二、填空题
-
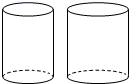
10. 如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2 , 且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,则甲的容积为 .
 11. ﹣3的相反数与﹣0.5的倒数的和是 .12. 如图, 是北偏东 方向的一条射线, ,则 的方位角是.
11. ﹣3的相反数与﹣0.5的倒数的和是 .12. 如图, 是北偏东 方向的一条射线, ,则 的方位角是.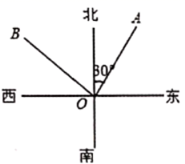 13. 在半径为1的圆中,圆心角是60°的扇形的面积是 .14. 若关于 的代数式 中不含有二次项,则k =.15. 如图,将一副三角尺的直角顶点重合,摆放在桌面上,若∠BOC=35°,则∠AOD=°.
13. 在半径为1的圆中,圆心角是60°的扇形的面积是 .14. 若关于 的代数式 中不含有二次项,则k =.15. 如图,将一副三角尺的直角顶点重合,摆放在桌面上,若∠BOC=35°,则∠AOD=°.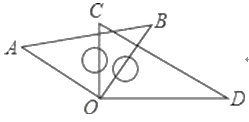 16. 为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:
16. 为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图: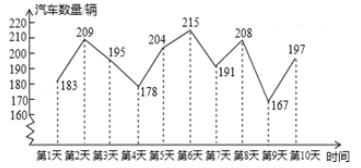
由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为天.
17. 如图是某几何体从不同方向看到的图形.若从正面看的高为10cm,从上面看的圆的直径为4cm,求这个几何体的侧面积(结果保留π)为 .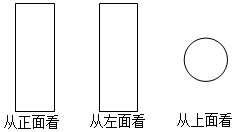 18. 如图,用一块长 .宽 的长方形纸板,和一块长 .宽 的长方形纸板,与一块正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则拼成的大正方形的面积是 .
18. 如图,用一块长 .宽 的长方形纸板,和一块长 .宽 的长方形纸板,与一块正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则拼成的大正方形的面积是 .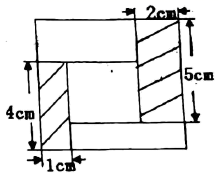
三、解答题
-
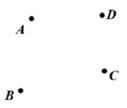
19. 计算:(1)、计算: ;(2)、计算: .20. 解方程(1)、(2)、21. 如图,已知 四点,按下列要求画图形:
( 1 )画射线 ;
( 2 )画直线 ;
( 3 )连接 ,并延长至 ,使得 .
 22. 老师设计了一个数学实验,给甲、乙、丙三名同学各一张写有已化为最简的代数式的卡片,规则是两位同学的代数式相减等于第三位同学的代数式,则实验成功.甲、乙、丙的卡片如图所示,丙的卡片有一部分看不清楚了.
22. 老师设计了一个数学实验,给甲、乙、丙三名同学各一张写有已化为最简的代数式的卡片,规则是两位同学的代数式相减等于第三位同学的代数式,则实验成功.甲、乙、丙的卡片如图所示,丙的卡片有一部分看不清楚了.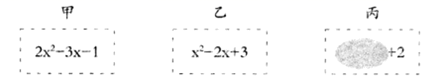 (1)、计算出甲减乙的结果,并判断甲减乙能否使实验成功;(2)、嘉淇发现丙减甲可以使实验成功,请求出丙的代数式.23. “文明城市,你我共建”一起助力太原市创建全国文明城市.下面是某校“数学之星”课外兴趣小组的同学们,在对 个自行车骑行规则进行调查时设计的问卷,
(1)、计算出甲减乙的结果,并判断甲减乙能否使实验成功;(2)、嘉淇发现丙减甲可以使实验成功,请求出丙的代数式.23. “文明城市,你我共建”一起助力太原市创建全国文明城市.下面是某校“数学之星”课外兴趣小组的同学们,在对 个自行车骑行规则进行调查时设计的问卷,自行车骑行规则知多少
您好:
我们来自课外兴趣小组,为了了解我市市民骑行自行车的安全意识,请您抽出一点时间填写这份问卷。谢谢合作!
规则1 不准在机动车道内骑行.( )
A.知道 B.不知道
规则2 不准闯红灯.( )
A知道 B.不知道
规则3 不准骑车带人.( )
A.知道 B.不知道
规则4 横过人行横道时不准骑行.( )
A.知道 B.不知道
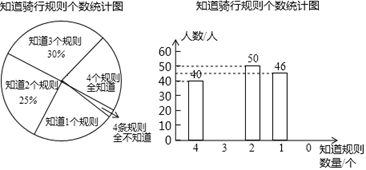
小组的同学们]随机抽取了部分市民进行调查,并将结果制成了如下两幅不完整的统计图.
请根据统计图解答下列问题:
(1)、求被调查的市民人数;(2)、在扇形统计图中,求“ 个规则全知道”所对圆心角的度数;(3)、请补全条形统计图;(4)、请根据调查结果,谈谈你的看法.24. 这个星期周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,每班人数都多于50人,票价每张20元,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:方案一:全体人员可打8折;方案2:若打9折,有7人可以免票.
(Ⅰ)2班有61名学生,他该选择哪个方案?
(Ⅱ)一班班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的,问你知道一班有几人吗?
25. 综合与实践:在数学综合与实践课上,老师以“出行方式的选择"为主题,请同学们发现和提出问题并分断和解决问题问题情境:随着互联网的普及和城市交通的多样化,人们出行的时间与方式有了更多的选择.某市有出租车.滴滴快车和神州专车三种网约车,收费标准见下图(该市规定网约车行驶的平均速度为 公里时)
 (1)、问题一:“奋进小组”提出的问题是:如果乘坐这三种网约车的里程数都是10公里.他们发现乘坐出租车最节省钱.费用为元;(2)、问题二:“质疑小组”提出了两个问题,请从 两个问题中任选一问做答,
(1)、问题一:“奋进小组”提出的问题是:如果乘坐这三种网约车的里程数都是10公里.他们发现乘坐出租车最节省钱.费用为元;(2)、问题二:“质疑小组”提出了两个问题,请从 两个问题中任选一问做答,A.从甲地到乙地,乘坐出租车比滴滴快车节省 元,求甲.乙两地间的里程数.
B.神州专车和滴滴快车对第一次下单的乘客有如下优惠活动:神州专车收费打八折,另外加 元的空车费;滴滴快车超过 公里收费立减 元.如果两位顾客都是第一次下单,分别乘坐神州专车、滴滴快车且收费相同,求这两位顾客乘车的里程数.