辽宁省大连市开发区2020-2021学年七年级上学期期末数学试题

试卷更新日期：2021-11-12 类型：期末考试

进入出卷网下载

一、单选题

1. 实数 $- 2$ 的绝对值是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 如图是一个正方体，则它的表面展开图可以是（　　）

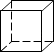A、 B、 C、 D、

查看试题解析
3. 将90 000 000用科学记数法表示为（）

A、9×10⁶ B、90×10⁶ C、9×10⁷ D、0.9×10⁸

查看试题解析
4. 下列式子中，是一元一次方程的是（）

A、3x+1=4x B、x+2＞1 C、x²－9=0 D、2x－3y=0

查看试题解析
5. 下列计算中，正确的是（）

A、3x－x=2x B、6y²－y²=5 C、b⁴+b³=b⁷ D、3x+4y=7xy

查看试题解析
6. 如果 $x = 2$ 是方程 $\frac{1}{2} x + a = - 1$ 的解，那么a的值是（）

A、0 B、2 C、 $- 2$ D、 $- 6$

查看试题解析
7.
如图，C、D是线段AB上的两点，且D是线段AC的中点．若AB=10cm，BC=4cm，则AD的长为（　　）

A、2cm B、3cm C、4cm D、6cm

查看试题解析
8. 某商店销售一批服装，每件售价150元，可获利25%，求这种服装的成本价．设这种服装的成本价为x元，则得到方程（）

A、 $x = 150 \times 25 %$ B、 $25 % \cdot x = 150$ C、 $(1 + 25 %) x = 150$ D、 $150 - x = 25 %$

查看试题解析
9. 下列作图语句中，叙述正确的是（）

A、延长线段AB到点C，使BC=AB B、画直线AB的中点C C、画直线AB=6cm D、延长射线OA到点B

查看试题解析
10. 若等式 $m + a = n - b$ 根据等式的性质变形得到 $m = n$ ，则 $a 、 b$ 满足的条件是（）

A、相等 B、互为倒数 C、互为相反数 D、无法确定

查看试题解析

二、填空题

11. 在1，-1，0， -2这几个数中，最小的数是．

查看试题解析
12. 我市一月某天早上气温为-6℃，中午上升了9℃，这天中午的温度是℃．

查看试题解析
13. 如图，点D是AB的中点，点E是BC的中点，若 $A C = 8 ， E C = 3$ 则AD= ．

查看试题解析
14. 若将一副三角板摆成如图的位置，则∠ $α$ 、∠ $β$ 的数量关系是．

查看试题解析
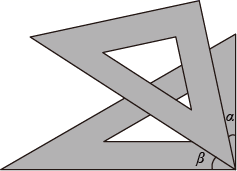15. 已知∠AOB=50°，∠BOC=30°，则∠AOC= ．

查看试题解析
16. 点A₀、A₁、A₂、A₃、…、A_n（n为自然数）都在数轴上．点A₁在原点A₀的左边，且A₁ A₀=1；点A₂在点A₁的右边，且A₂A₁=2；点A₃在点A₂的左边，且A₃A₂=3；点A₄在点A₃的右边，且A₄A₃=4；…．依照上述规律，A₂₀₁₇A₂₀₁₆= ．

查看试题解析

三、解答题

17. 计算： $2 \times {(- 3)}^{3} - 4^{2} \times (- 3)$ ．

查看试题解析
18. 已知A、B、C、D四点，根据下列要求画图：

（ 1 ）画射线AD；

（ 2 ）画直线AB；

（ 3 ）连接AC、BD交于点O．

查看试题解析
19. 解下列方程： $\frac{3 x - 1}{2} = \frac{4 x + 2}{5} - 1$ ．

查看试题解析
20. 先化简，再求值： $3 (- 2 a b + 3 a) - (2 a - b) + 6 a b$ ，其中 $a = - 1 ， b = 3$ ．

查看试题解析
21. 某检修小组从A地出发，在东西方向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中五次行驶记录如下（单位：千米）：

第一次

第二次

第三次

第四次

第五次

﹣3

8

﹣9

+10

﹣2

(1)、在第次记录时距A地最远；

(2)、收工时距A地千米；

(3)、若每千米耗油0.3升，每升汽油需6.5元，问检修小组工作一天需汽油费多少元？

查看试题解析
22. 元旦期间，我市某超市从外地购进一批水果600千克，进货价为2元/千克，该超市将其中m千克优等品以4元/千克对外出售，余下的二等品则以2.5元/千克的价格出售，全部售出．

(1)、①二等品为千克（用含m的代数式表示）；
②若不计其他成本，用含m的代数式表示第一批水果的总利润（总售价﹣总进价=总利润）

(2)、根据市场需要，又购进了第二批水果800千克，这一次的进货单价比第一批少了0.5元．其中优等品比第一批多了n千克，超市以3.5元/千克的价格出售优等品，余下的二等品在这批进货单价的基础上每千克加价1元后全部卖完，若第一批水果的总利润是第二批水果的总利润的 $\frac{3}{8}$ ，求m、n之间的数量关系．

查看试题解析
23. 点O为直线AB上一点，过点O作射线OC，使∠AOC=120°，一直角三角板的直角顶点放在点O处．

(1)、如图1，将三角板DOE的一边OD与射线OB重合时，则∠COD= °；

(2)、如图2，将图1中的三角板DOE绕点O逆时针旋转一定角度，当OC恰好是∠BOE的角平分线时，求∠COD的度数；

(3)、将图1中的三角尺DOE绕点O逆时针旋转旋转 $α$ 度，OE始终在∠AOC的内部，在旋转的过程中，能否使∠AOE=3∠COD？若能，求出 $α$ 的度数；若不能，说明理由．

查看试题解析
24. 如图，数轴上A、B两点对应的数分别为6和10．点P从原点O出发，以每秒3个单位长度的速度沿数轴正方向运动，同时点Q从点A出发，以每秒1个单位长度的速度沿数轴正方向运动．设运动时间为t秒．

(1)、线段AB的长度是，点Q对应的数是；

(2)、当点P、Q重合时，求t的值；

(3)、当 $P Q = \frac{1}{2} B Q$ 时，求t的值．

查看试题解析

第一次	第二次	第三次	第四次	第五次
﹣3	8	﹣9	+10	﹣2