辽宁省大连市高新园区2020-2021学年七年级上学期期末数学试题
试卷更新日期:2021-11-12 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、32. 下列图形都是由六个相同的正方形组成的,经过折叠不能围成正方体的是( )A、
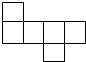 B、
B、 C、
C、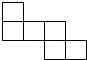 D、
D、 3. 我国首艘国产航母在大连下水,其排水量约为65000吨,将65000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
3. 我国首艘国产航母在大连下水,其排水量约为65000吨,将65000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( ) A、 B、 C、 D、6. 如果方程 与方程 的解相同,则k的值为( )A、2 B、 C、4 D、7.
A、 B、 C、 D、6. 如果方程 与方程 的解相同,则k的值为( )A、2 B、 C、4 D、7.如图,AB=8cm,AD=BC=5cm,则CD等于( )
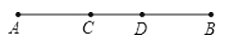 A、1cm B、2cm C、3cm D、4cm8. 已知 ,则式子 的值为( )A、5 B、 C、1 D、9. 小王家今年甲苹果园有苹果9000千克,乙苹果园有苹果6000千克,因客户订单要求,需要从乙苹果园运部分苹果到甲苹果园,使甲苹果园苹果数量刚好是乙苹果园的2倍.设从乙苹果园运苹果x千克到甲苹果园,则可列方程为( )A、 B、 C、 D、10. 如图,已知 平分 ,且 ,则 的度数为( )
A、1cm B、2cm C、3cm D、4cm8. 已知 ,则式子 的值为( )A、5 B、 C、1 D、9. 小王家今年甲苹果园有苹果9000千克,乙苹果园有苹果6000千克,因客户订单要求,需要从乙苹果园运部分苹果到甲苹果园,使甲苹果园苹果数量刚好是乙苹果园的2倍.设从乙苹果园运苹果x千克到甲苹果园,则可列方程为( )A、 B、 C、 D、10. 如图,已知 平分 ,且 ,则 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在 这四个数中,最小的数是.12. 与 互余, ,则 .13. 若 ,则 .14. 《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家?设城中有x户人家,则可以列得方程为 .15. 如图,两只船A,B分别在海岛O的北偏东 和东南方向,则两只船A,B与海岛O形成的夹角 的度数为 .
 16. 如图,点C是线段 的中点,点E在线段 上,点D是线段 的中点, ,则线段 的长为(用含a的式子表示).
16. 如图,点C是线段 的中点,点E在线段 上,点D是线段 的中点, ,则线段 的长为(用含a的式子表示).
三、解答题
-
17.(1)、计算: ;(2)、解方程: .18. 先化简,再求值: ,其中 .19. 如图:
 (1)、如图1,已知平面上A,B,C三点,请按照下列语句画出图形.
(1)、如图1,已知平面上A,B,C三点,请按照下列语句画出图形.①连接 ;
②画射线 ;
③画直线 ;
(2)、如图2,已知线段 .①画图:延长 到C,使 ;
②若D为 的中点,且 ,求线段 的长.
20. 有10箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下表:与标准重量的差值(单位:千克)
0
1
2.5
箱数
1
3
2
1
1
2
(1)、10箱苹果中,最轻的一箱比最重的一箱少多少千克?(2)、与标准重量比较,10箱苹果总计超过或不足多少千克?(3)、若苹果售价每千克5元,则这10箱苹果全部售出可以收入多少元?21. 一件商品按进价提高30%后标价,然后打八折卖出,结果仍能获利20元,这件商品的进价是多少元?22. 设x、y是任意两个有理数,规定x与y之间的一种运算 为:(1)、填空: , ;(2)、若 ,求m的值.23. 已知点D为线段 的中点,点C在线段 上.(1)、如图1,若 ,求线段 的长; (2)、如图2,若 ,点E为 中点, ,求线段 的长.
(2)、如图2,若 ,点E为 中点, ,求线段 的长. 24. 下表是中国移动两种“ G套餐”计费方式(月租费固定收,主叫不超过主叫时间,流量不超上网流量不再收费,主叫超时和上网超流量部分加收超时费和超流量费)
24. 下表是中国移动两种“ G套餐”计费方式(月租费固定收,主叫不超过主叫时间,流量不超上网流量不再收费,主叫超时和上网超流量部分加收超时费和超流量费)月租费
(元)
主叫通话
(分钟)
上网流量
(G)
接听
主叫超时部分
(元/分钟)
超出流量部分
(元/G)
方式一
38
200
3
免费
0.15
10
方式二
60
300
5
免费
0.10
8
(1)、若某月小张主叫通话时间为260分钟,上网流量为4G,则他按方式一计费需元,按方式二计费需元;(2)、若某月小张按方式二计费需78元,主叫通话时间为320分钟,则小张该月上网流量为多少G?(3)、若某月小张上网流量为 G,是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等?若存在,请求出t的值;若不存在,请说明理由.25. 如图1,在 内部作射线 , , 在 左侧,且 .(1)、图1中,若 平分 平分 ,则 ; (2)、如图2, 平分 ,探究 与 之间的数量关系,并证明;
(2)、如图2, 平分 ,探究 与 之间的数量关系,并证明; (3)、设 ,过点O作射线 ,使 为 的平分线,再作 的角平分线 ,若 ,画出相应的图形并求 的度数(用含m的式子表示).26. 如图,数轴上点A在原点左侧,点B在原点右侧,且 ,动点P、Q分别从A、B两点同时出发,都向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,当点P与点Q重合时,P,Q两点停止运动.设运动时间为t秒.
(3)、设 ,过点O作射线 ,使 为 的平分线,再作 的角平分线 ,若 ,画出相应的图形并求 的度数(用含m的式子表示).26. 如图,数轴上点A在原点左侧,点B在原点右侧,且 ,动点P、Q分别从A、B两点同时出发,都向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,当点P与点Q重合时,P,Q两点停止运动.设运动时间为t秒. (1)、若点A表示的数为 ,则点B表示的数为 , 线段 中点表示的数为;(2)、在(1)的条件下,若 ,求t的值;(3)、当点P在线段 上运动时,若 ,请探究线段 与线段 之间的数量关系,并说明理由.
(1)、若点A表示的数为 ,则点B表示的数为 , 线段 中点表示的数为;(2)、在(1)的条件下,若 ,求t的值;(3)、当点P在线段 上运动时,若 ,请探究线段 与线段 之间的数量关系,并说明理由.