山西省运城市2022届高三上学期物理10月质量检测试卷

试卷更新日期：2021-11-11 类型：月考试卷

进入出卷网下载

一、单选题

1. 伽利略从斜面实验外推到自由落体运动的情景模型如图所示，下列说法符合史实的是（）

A、伽利略先猜想下落物体的速度随时间均匀增加，然后通过斜面实验直接得出 $v \propto t$ B、伽利略通过斜面实验得出：从静止开始小球必须沿光滑的斜面运动才有 $s \propto t^{2}$ C、伽利略采用“冲淡”重力的方法，实质是增大小球的位移，延长小球的运动时间 D、伽利略发现，改变斜面的倾角， $s \propto t^{2}$ 依然成立，斜面的倾角越大， $\frac{s}{t^{2}}$ 越大

查看试题解析
2. 如图所示，光滑斜面上用细线拴着的匀质小球处于静止状态，细线水平且延长线经过球心O，小球与斜面的接触点为A，下列说法正确的是（）

A、细线的拉力不可能等于小球的重力 B、细线的拉力一定小于斜面对小球的支持力 C、若细线长度等于小球半径，则细线拉力等于小球重力 D、若细线长度等于小球半径．则细线拉力等于小球重力的一半

查看试题解析
3. 如图所示，小船从河岸的O点沿虚线匀速运动到河对岸的P点，河水的流速 $v_{水}$ 、船在静水中的速度 $v_{静}$ 与虚线的夹角分别为 $α$ 、 $β$ 。河宽为d，且 $v_{静}$ 、 $v_{水}$ 的大小不变，下列说法正确的是（）

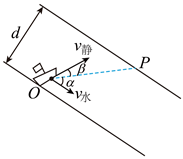A、渡河时间由 $v_{静}$ 、 $β$ 以及河宽d决定 B、当 $α + β = 45 °$ ，渡河的时间为 $\frac{\sqrt{2} d}{2 v_{静}}$ C、 $v_{静}$ 、 $v_{水}$ 在垂直虚线方向的分量等大反向 D、船的实际运行速度 $v = v_{水} \sin α + v_{静} \sin β$

查看试题解析
4. 如图所示，三个质量相等的物块A、B、C组合在一起，A带有定滑轮放在光滑的水平面上，跨过定滑轮的轻质细线连接B、C，A与B之间的动摩擦因数为0.7，滑轮与细线、轮轴之间以及A、C之间的摩擦和定滑轮的质量忽略不计，最大静摩擦力等于滑动摩擦力。水平推力F作用在A上，为了使三个物块相对静止，则F的最大值与最小值之比为（）

A、3：1 B、17：3 C、16：3 D、6：1

查看试题解析
5. 质量均为m的物体甲和乙，从静止开始做加速直线运动的a-t和a-x关系图象分别如图1、2所示。分析图象，则下列说法正确的是（）

A、甲、乙的运动性质相同，加速度随时间都均匀增大 B、甲、乙都做匀变速直线运动 C、 $t_{1}$ 时刻甲的动能为 $\frac{m {(a_{0} + a_{1})}^{2} t_{1}^{2}}{8}$ D、乙运动到 $x_{1}$ 处的速度为 $\sqrt{\frac{(a_{0} + a_{1}) x_{1}}{2}}$

查看试题解析
6. 如图所示，小球甲从斜面的A点水平抛出，经过时间 $t_{1}$ 落到斜面上的B点。带有小孔的水平挡板一端固定在斜面的B点，小孔与B点的距离等于甲平抛运动的水平位移。将小球乙从斜面的A点水平抛出，正好通过小孔，经过时间 $t_{2}$ 落到斜面上的C点。乙从A点到达小孔处需要的时间为 $t_{0}$ 。小孔与小球的大小均可忽略不计，则 $t_{1}$ 、 $t_{0}$ 、 $t_{2}$ 的比值为（）

A、1：1：2 B、 $1 ： 1 ： \sqrt{2}$ C、 $1 ： 1 ： \sqrt{3}$ D、1：1：3

查看试题解析

二、多选题

7. 如图所示，一细线两端固定在竖直轴上，光滑的圆环穿过细线，在水平面内绕竖直轴上的O点做匀速圆周运动，细线的上部分1与竖直轴的夹角为 $α$ ，下部分2与竖直轴的夹角为 $β$ ，重力加速度g取 $10 {m/s}^{2}$ ，下列说法正确的是（）

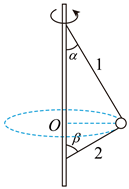A、细线的上部分1与下部分2对圆环的拉力大小不相等 B、夹角 $α$ 一定小于夹角 $β$ C、若 $α = 37 °$ 、 $β = 53 °$ （ $\sin 37 ° = 0.6$ ， $\cos 37 ° = 0.8$ ），则圆环的加速度大小为 ${12m/s}^{2}$ D、若 $α = 37 °$ 、 $β = 53 °$ ，圆环到O点的距离为0.7m，则圆环的周期为 $\frac{π}{5} s$

查看试题解析
8. 一探测器从某天体表面开始先竖直向上做初速度为0的匀加速直线运动，上升到距离是此天体半径的 $\frac{1}{4}$ ，此过程的起点、终点探测器发动机提供的推力差值为 $Δ F$ 。已知该天体表面的重力加速度为 $g_{0}$ ，引力常量为G，忽略天体的自转，下列说法正确的是（）

A、探测器的质量为 $\frac{25 Δ F}{9 g_{0}}$ B、探测器匀加速直线运动的加速度为 $\frac{Δ F}{m}$ C、若此天体的质量为M，则天体的第一宇宙速度为 $\sqrt{G M g_{0}}$ D、若天体的半径为R，探测器匀加速的加速度为a，则在终点探测器的动能为 $\frac{25 Δ F R a}{36 g_{0}}$

查看试题解析
9. 如图甲所示，轻质弹簧的下端固定在水平地面上，上端静置一物体（与弹簧不粘连），现用竖直向上的拉力F作用在物体上，使物体向上做匀加速直线运动，拉力F与物体的位移x的关系如图乙所示，重力加速度g取 ${10m/s}^{2}$ ，下列说法正确的是（）

A、物体的加速度为 ${1m/s}^{2}$ B、弹簧的劲度系数为20N/m C、经过 $\sqrt{2} s$ 物体与弹簧分离 D、从物体开始运动到与弹簧分离，弹簧与物体组成的系统机械能增加了3.5J

查看试题解析
10. 如图所示，半径为4m的光滑半圆轨道固定在水平面上，质量为0.25kg的小球从与圆心O的等高处A点由静止释放，当小球落到轨道的B点与轨道碰撞，沿OB向下方向的分速度突减为0，垂直OB向下方向分速度不变。经过最低点C后，到达轨道左侧最大高度处D点， $∠ A O B = 53 °$ ，重力加速度g取 ${10m/s}^{2}$ ， $\sin 53 ° = 0.8$ ， $\cos 53 ° = 0.6$ ，下列说法正确的是（）

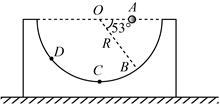A、在B点，小球与轨道碰撞损失的机械能为5.12J B、小球与轨道在B点碰撞前、后瞬间，重力功率的差值为8W C、在C点，轨道对小球的支持力大小为2.44N D、D，B两点的竖直高度差为1.152m

查看试题解析

三、实验题

11. 实验小组用如图甲所示的装置做“探究功与速度变化的关系”实验。将小车在一条橡皮筋作用下弹出时，橡皮筋对小车做的功记为 $W_{0}$ ，当用2条、3条…完全相同的橡皮筋并在一起且伸长的长度保持与第一次相同进行第2次、第3次…实验时，用速度传感器测出小车速度v和速度的平方 $v^{2}$ ，将数据输入电脑处理，得到如图乙所示的 $v^{2} - t$ 图象，由图象可以读出每次实验时小车获得的最大速度的平方分别为a、b、c，回答下列问题：

(1)、本实验（填“需要”或“不需要”）平衡摩擦力。

(2)、若 $a ： b ： c = 1 ： 2 ： 3$ ，可以得出橡皮筋对小车做的功W与小车最大速度的平方 $v^{2}$ 成（填“正比”或“反比”）。

(3)、多次实验后，做出很多种图象，其中一种 $W - v^{2}$ 图象如图丙所示，其中一种W-v图象如图丁所示，丙图的图线平滑延长不过坐标原点的原因是；丁图的图线平滑延长不过坐标原点的原因是。

查看试题解析
12. 某同学利用图甲装置探究“系统的机械能守恒”，实验过程如下：

（1）该同学首先利用游标卡尺测量遮光条的宽度，如图乙所示宽度d= cm。
（2）按图甲竖直悬挂好轻质弹簧，将轻质遮光条水平固定在弹簧下端，测出此时弹簧的长度 $x_{0}$ ；在铁架台上固定一个位置指针，标示出弹簧不挂钩码时遮光条下边缘的位置，用轻质细线在弹簧下方挂上钩码，测量出平衡时弹簧的长度x，并按图所示将光电门的中心线调至与遮光条下边缘同一高度。
（3）用手缓慢地将钩码向上托起，直至遮光条恰好回到弹簧原长标记指针的等高处（保持细线竖直），将钩码由静止释放，记下遮光条经过光电门的时间 $Δ t$ 。
（4）多次改变钩码个数，重复步骤（2）（3），得到多组数据，作出 $(x - x_{0}) -$ 图象如图丙所示（填选项前的字母序号）。已知当地重力加速度为g，则当图线斜率等于（用d和g表示）时，可得系统的机械能守恒。（弹簧的弹性势能表达式为 $E_{p} = \frac{1}{2} k {x^{'}}^{2}$ ，其中k为弹簧的劲度系数， $x^{'}$ 为弹簧的形变量）

A． $Δ t$ B． $Δ t^{2}$ C． $\frac{1}{Δ t}$ D． $\frac{1}{Δ t^{2}}$

查看试题解析

四、解答题

13. 如图所示，轻质细线跨过轻质定滑轮，两端分别悬挂质量 $m_{1} = 4 kg$ 、 $m_{2} = 0.5 kg$ 的甲、乙两球，两球由静止释放时高度差 $h = 6 m$ ，经过一段时间 $Δ t$ ，甲、乙正好处于同一高度，甲、乙均可视为质点，所受的空气阻力大小相同均恒为4N，滑轮与轴、细线之间摩擦忽略不计，重力加速度g取 ${10m/s}^{2}$ ，求：

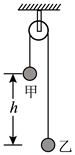(1)、 $Δ t$ 的值；

(2)、该过程中系统机械能的变化量。

查看试题解析
14. 如图所示，轻质细线把质量 $m = 0.5 kg$ 的物体连接在墙上，物体与墙之间夹有被压缩的轻质弹簧（物体与弹簧不拴接）静止在水平面上。水平面P点的右侧光滑、左侧粗糙，某时刻烧断细线，物体被弹开后从P点向左减速到达B点接着沿着斜面向上运动，达到A点速度恰好为0，接着物体从A点恰好可以返回到P点，物体与PB之间、BA之间的动摩擦因数均为 $μ$ ，斜面AB与水平面间夹角为53°，A到水平面高度为 $h = 2.4 m$ ，且 $A B = B P$ 。不计物体在斜面与水平面转折处的能量损失，重力加速度g取 ${10m/s}^{2}$ ， $\sin 53 ° = 0.8$ ， $\cos 53 ° = 0.6$ ，求：

(1)、弹簧释放的弹性势能 $E_{p}$ ；

(2)、动摩擦因数 $μ$ 。

查看试题解析
15. 质量为m的小球，从A点以初速度 $v_{0}$ 竖直向上抛出，同时受到恒定的水平向左的风力作用，经过一段时间到达最高点C，此过程水平方向的分位移与竖直方向的分位移之比为3：4。已知小球在B点时速度最小，重力加速度为g，求：

(1)、小球所受合力的大小及合力与水平方向间夹角的正切值；

(2)、小球在B点的速度大小与在C点的速度大小的比值及从A到B的运动时间。

查看试题解析
16. 如图所示，质量为m的小球（视为质点）用长为L的轻质细线悬挂在 $O_{1}$ 点，细线能承受的最大拉力 $T_{m} = 30 N$ ，将细线拉直使小球与 $O_{1}$ 等高，由静止释放，运动到最低点B时，细线刚好被拉断，小球立即沿着竖直放置的半径为 $r = 2 m$ 的光滑半圆轨道向上运动，恰能通过最高点C，小球离开C点后，当回到与B点等高的D点时，正好无碰撞沿着竖直放置的半径为R的光滑圆弧轨道继续向下运动， $O_{3}$ 是圆弧轨道圆心，E是最低点，半径 $O_{3} D$ 与竖直半径 $O_{3} E$ 的夹角为 $θ$ ，小球通过D点时，轨道对小球的弹力为 $F_{D} = (25 + 2 \sqrt{5}) N$ ，重力加速g取 ${10m/s}^{2}$ ，空气的阻力忽略不计，求：（结果可保留根号）

(1)、小球质量m及细线长度L；

(2)、 $θ$ 的余弦值；

(3)、圆弧轨道的半径R及小球在E点的向心加速度大小。

查看试题解析