浙教版数学八上第5章 一次函数优生综合题特训
试卷更新日期:2021-11-11 类型:复习试卷
一、综合题
-
1. 下图为小强在早晨S时从城市出发到郊外所走的路程与时间的变化图
 根据图回答问题:
根据图回答问题:
 (1)、图象中自变量是 , 因变量是 ;(2)、9时,10时30分,12时小强所走的路程分别是千米,千米,千米;(3)、小强休息了多长时间:小时;(4)、求小强从休息后直至到达目的地这段时间的平均速度.2. 地壳的厚度约为8到40km , 在地表以下不太深的地方,温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度.(1)、在这个变化过程中,自变量和因变量分别是什么?(2)、如果地表温度为2℃,计算当x为5km时地壳的温度.3. 如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,a),点B的坐标为(b , 0),且a , b满足 .
(1)、图象中自变量是 , 因变量是 ;(2)、9时,10时30分,12时小强所走的路程分别是千米,千米,千米;(3)、小强休息了多长时间:小时;(4)、求小强从休息后直至到达目的地这段时间的平均速度.2. 地壳的厚度约为8到40km , 在地表以下不太深的地方,温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度.(1)、在这个变化过程中,自变量和因变量分别是什么?(2)、如果地表温度为2℃,计算当x为5km时地壳的温度.3. 如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,a),点B的坐标为(b , 0),且a , b满足 .
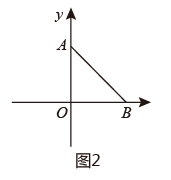
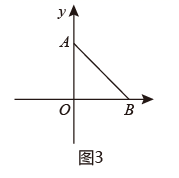 (1)、求点A、点B的坐标;(2)、动点P从点B出发,以每秒1个单位长度的速度向终点O匀速运动,连接AP , 过点B作BQ⊥AP交AP的延长线于点Q , 延长BQ交y轴于点C , 设点P的运动时间为t秒, BOC的面积为S , 求S与t之间的关系式;(3)、在(2)的条件下,作射线OG平分∠BOC交BC于点G , 当 时,求t的值和G点坐标.4. 如图,在平面直角坐标系中,点A坐标为(0,3),点C坐标为(6,0),AB x轴,且OA=AB,动点P从点O出发以2个单位/秒的速度沿O→A→B→C的路线匀速运动,运动到点C时终止.过点P作PQ⊥x轴,垂足为Q,设点P的运动时间为x(s),线段PQ的长为y.
(1)、求点A、点B的坐标;(2)、动点P从点B出发,以每秒1个单位长度的速度向终点O匀速运动,连接AP , 过点B作BQ⊥AP交AP的延长线于点Q , 延长BQ交y轴于点C , 设点P的运动时间为t秒, BOC的面积为S , 求S与t之间的关系式;(3)、在(2)的条件下,作射线OG平分∠BOC交BC于点G , 当 时,求t的值和G点坐标.4. 如图,在平面直角坐标系中,点A坐标为(0,3),点C坐标为(6,0),AB x轴,且OA=AB,动点P从点O出发以2个单位/秒的速度沿O→A→B→C的路线匀速运动,运动到点C时终止.过点P作PQ⊥x轴,垂足为Q,设点P的运动时间为x(s),线段PQ的长为y.
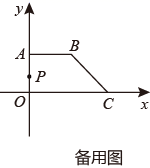 (1)、求∠C的度数;(2)、求y与x的函数关系式.5. 如图,已知正方形 的边长为 ,点 为边 上的一个动点(不与点 、 重合),将正方形纸片翻折,使得点 落在点 处,点 落在点 处, 交边 于点 ,折痕为 ,联结 交边 于点 .
(1)、求∠C的度数;(2)、求y与x的函数关系式.5. 如图,已知正方形 的边长为 ,点 为边 上的一个动点(不与点 、 重合),将正方形纸片翻折,使得点 落在点 处,点 落在点 处, 交边 于点 ,折痕为 ,联结 交边 于点 .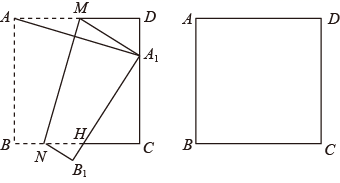 (1)、求证: .(2)、当 在边 的运动时,设 ,梯形 的面积为 ,求 与 之间的函数解析式,并写出定义域.6. 如图,在平面直角坐标系中,直线l1: 分别交x、y轴于B、A两点,将△AOB沿直线l2: 折叠,点B落在y细的点C处.
(1)、求证: .(2)、当 在边 的运动时,设 ,梯形 的面积为 ,求 与 之间的函数解析式,并写出定义域.6. 如图,在平面直角坐标系中,直线l1: 分别交x、y轴于B、A两点,将△AOB沿直线l2: 折叠,点B落在y细的点C处.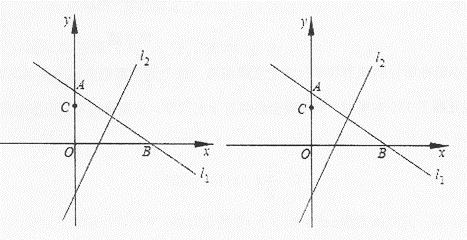 (1)、点C的坐标为:(2)、若点D沿射线BA运动,连接OD,当△CDB 与△CDO面积相等时,求直线OD的解析式;(3)、在(2)的条件下,当点D在第一象限时,沿x轴平移直线OD,分别交x,y轴于点E,F,在平面直角坐标系中,是否存在点M(m,3)和点P,使四边形EFMP为正方形?若存在,求出点P的坐标;若不存在,说明理由.7. 如图,在平面直角坐标系xOy中,点A在y轴的正半轴上,点B在x轴的正半轴上,OA=OB=10.
(1)、点C的坐标为:(2)、若点D沿射线BA运动,连接OD,当△CDB 与△CDO面积相等时,求直线OD的解析式;(3)、在(2)的条件下,当点D在第一象限时,沿x轴平移直线OD,分别交x,y轴于点E,F,在平面直角坐标系中,是否存在点M(m,3)和点P,使四边形EFMP为正方形?若存在,求出点P的坐标;若不存在,说明理由.7. 如图,在平面直角坐标系xOy中,点A在y轴的正半轴上,点B在x轴的正半轴上,OA=OB=10.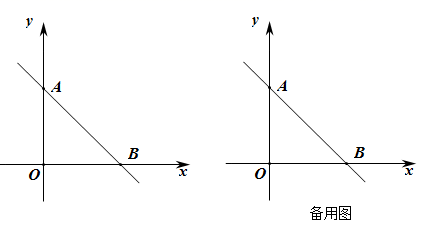 (1)、求直线AB的解析式;(2)、若点P是直线AB上的动点,当S△OBP= S△OAP时,求点P的坐标;(3)、将直线AB向下平移10个单位长度得到直线l,点M,N是直线l上的动点(M,N的横坐标分别是xM , xN , 且xM<xN),MN=4 ,求四边形ABNM的周长的最小值,并说明理由.8. 在平面直角坐标系 中,直线 经过 和 两点.
(1)、求直线AB的解析式;(2)、若点P是直线AB上的动点,当S△OBP= S△OAP时,求点P的坐标;(3)、将直线AB向下平移10个单位长度得到直线l,点M,N是直线l上的动点(M,N的横坐标分别是xM , xN , 且xM<xN),MN=4 ,求四边形ABNM的周长的最小值,并说明理由.8. 在平面直角坐标系 中,直线 经过 和 两点.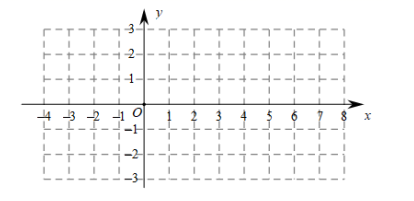 (1)、求直线的表达式;(2)、如果横、纵坐标都是整数的点叫作整点,直线 和直线 关于 轴对称,过点 作垂直于 轴的直线 与 和 的区域为“ ”(不包含边界).
(1)、求直线的表达式;(2)、如果横、纵坐标都是整数的点叫作整点,直线 和直线 关于 轴对称,过点 作垂直于 轴的直线 与 和 的区域为“ ”(不包含边界).①当 时,求区域“ ”内整点的个数;
②如果区域“ ”内恰好有 个整点,直接写出 的取值范围.
9. 如图1,在平面直角坐标系中,点 是坐标原点,直线 交 轴于点 ,交 轴于点 ,且 .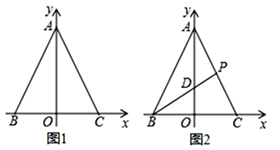 (1)、求直线 的解析式;(2)、如图2,点 在线段 上(不与 重合),连接 交 于点 ,设点 的横坐标为 , 的面积为 ,求 与 之间的函数解析式;(3)、在图2中, 时,求 的面积.10. 如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,4)经过点O、点C作直线l , 将直线l沿y轴上下平移.
(1)、求直线 的解析式;(2)、如图2,点 在线段 上(不与 重合),连接 交 于点 ,设点 的横坐标为 , 的面积为 ,求 与 之间的函数解析式;(3)、在图2中, 时,求 的面积.10. 如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,4)经过点O、点C作直线l , 将直线l沿y轴上下平移. (1)、当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;(2)、当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F , 连接BE、BF , 求△BEF的面积.11. 如图1,在平面直角坐标系中,直线y=﹣ x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)、当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;(2)、当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F , 连接BE、BF , 求△BEF的面积.11. 如图1,在平面直角坐标系中,直线y=﹣ x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.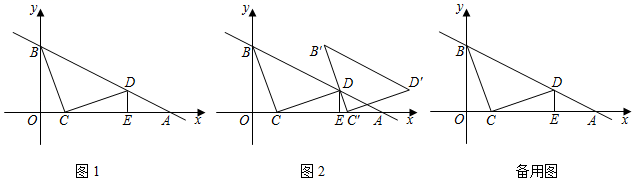 (1)、求证:△BOC≌△CED;(2)、如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)、若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.12. 如图,在平面直角坐标系中,直线AB交x轴于点A(﹣2,0)(0,4),直线y=kx+b经过点B且交x轴正半轴于点C , 已知△ABC面积为10.
(1)、求证:△BOC≌△CED;(2)、如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)、若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.12. 如图,在平面直角坐标系中,直线AB交x轴于点A(﹣2,0)(0,4),直线y=kx+b经过点B且交x轴正半轴于点C , 已知△ABC面积为10.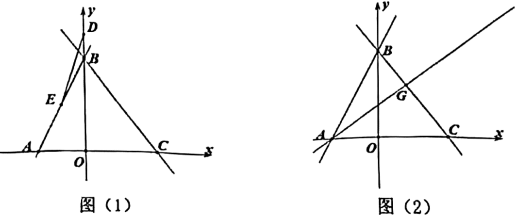 (1)、点C的坐标是( , ),直线BC的表达式是 ;(2)、如图1,点E为线段AB中点,点D为y轴上一动点,以DE为直角边作等腰直角三角形△EDF , 且DE=DF , 当点F落在直线BC上时,求点D的坐标;(3)、如图2,若G为线段BC上一点,且满足S△ABG=S△ABO , 点M为直线AG上一动点,在x轴上是否存在点N , 使以点B,C,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.13. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)、点C的坐标是( , ),直线BC的表达式是 ;(2)、如图1,点E为线段AB中点,点D为y轴上一动点,以DE为直角边作等腰直角三角形△EDF , 且DE=DF , 当点F落在直线BC上时,求点D的坐标;(3)、如图2,若G为线段BC上一点,且满足S△ABG=S△ABO , 点M为直线AG上一动点,在x轴上是否存在点N , 使以点B,C,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.13. 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题: (1)、慢车的速度为km/h,快车的速度为km/h;(2)、解释图中点D的实际意义并求出点D的坐标;(3)、求快车出发多少时间时,两车之间的距离为300km?14. 如图,直线y=2x-1与x轴、y轴分别交于B、C两点
(1)、慢车的速度为km/h,快车的速度为km/h;(2)、解释图中点D的实际意义并求出点D的坐标;(3)、求快车出发多少时间时,两车之间的距离为300km?14. 如图,直线y=2x-1与x轴、y轴分别交于B、C两点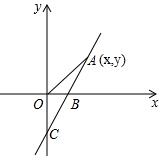 (1)、求点B的坐标;(2)、点A(x,y)是直线y= 2x-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、探究:①当点A的坐标是多少时,△AOB的面积为 ,并说明理由;
(1)、求点B的坐标;(2)、点A(x,y)是直线y= 2x-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、探究:①当点A的坐标是多少时,△AOB的面积为 ,并说明理由;②在①成立的情况下,x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请写出满足条件的三个P点坐标即可;若不存在,请说明理由。
15. 如图,直线y=kx+6(k≠0)与x轴、y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0).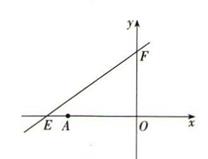 (1)、求k的值;(2)、若点P(x,y)是直线y=kx+6(k≠0)在第二象限内的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)、在(2)的情况下,当点P运动到什么位置时,△OPA的面积为 ?16. 探究活动一:
(1)、求k的值;(2)、若点P(x,y)是直线y=kx+6(k≠0)在第二象限内的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)、在(2)的情况下,当点P运动到什么位置时,△OPA的面积为 ?16. 探究活动一: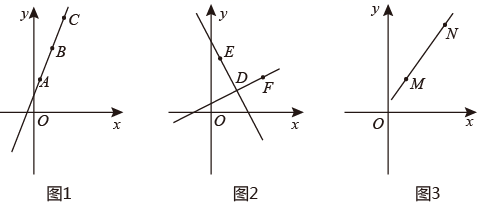
如图1,某数学兴趣小组在研究直线上点的坐标规律时,发现在直线 上的三点 , , ,有 , , ,兴趣小组提出猜想:若直线 上任意两点 , ,则 是定值.通过多次验证和查阅资料得知,猜想成立, 是定值,并且是直线 中的 ,叫做这条直线的斜率.
(1)、请你应用以上规律直接写出过 , 两点的直线 的斜率 .(2)、探究活动二: 数学兴趣小组继续深入研究直线的“斜率”问题,得到正确结论:当任意两条不和坐标轴平行的直线互相垂直时,这两条直线的斜率之积是定值.
如图2,直线 与直线 垂直于点 ,且 , , .请求出直线 与直线 的斜率之积.并写出你发现的结论.(3)、综合应用:
如图3, , ,请结合探究活动二的结论,求出过点 且与直线 垂直的直线的解析式.17. 某车间甲、乙两名工人分别生产同种零件,他们生产的零件数量y(个)与生产时间t(小时)之间的关系如图所示(其中实线表示甲,虚线表示乙,且甲因机器故障停产了一段时间).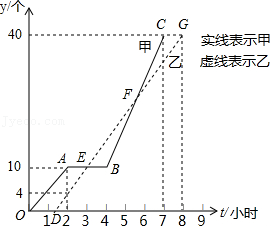 (1)、甲、乙中,先完成40个零件的生产任务.(2)、甲在因机器故障停产之前,每小时生产个零件.(3)、甲故障排除之后以原来速度的两倍重新开始生产,则甲停产了小时.(4)、在第一次甲乙生产零件总数在同一时刻相同到甲完工这段时间,什么时候甲乙生产的零件总数相差3个?18. 如图,在平面直角坐标系中,点 ,点 ,点 关于 轴的对称点为 .
(1)、甲、乙中,先完成40个零件的生产任务.(2)、甲在因机器故障停产之前,每小时生产个零件.(3)、甲故障排除之后以原来速度的两倍重新开始生产,则甲停产了小时.(4)、在第一次甲乙生产零件总数在同一时刻相同到甲完工这段时间,什么时候甲乙生产的零件总数相差3个?18. 如图,在平面直角坐标系中,点 ,点 ,点 关于 轴的对称点为 . (1)、点 的坐标为;(2)、已知一次函数的图象经过点 与 ,求这个一次函数的解析式;(3)、点 是 轴上的一个动点,当 时, 的周长最小;(4)、点 , 是 轴上的两个动点,当 时,四边形 的周长最小;(5)、点 ,点 分别是 轴和 轴上的动点,当四边形 的周长最小时, , 此时四边形 的面积为 .19. 如图,在平面直角坐标系 中,直线 与 轴、 轴分别交于 、 两点,点 在线段 上,且 .
(1)、点 的坐标为;(2)、已知一次函数的图象经过点 与 ,求这个一次函数的解析式;(3)、点 是 轴上的一个动点,当 时, 的周长最小;(4)、点 , 是 轴上的两个动点,当 时,四边形 的周长最小;(5)、点 ,点 分别是 轴和 轴上的动点,当四边形 的周长最小时, , 此时四边形 的面积为 .19. 如图,在平面直角坐标系 中,直线 与 轴、 轴分别交于 、 两点,点 在线段 上,且 .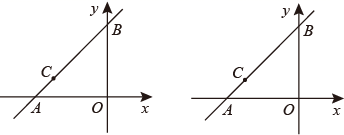 (1)、求点 的坐标;(2)、在坐标平面内是否存在点 ,使得以 、 、 、 为顶点的四边形是等腰梯形?若存在,请直接写出点 的坐标;若不存在,请说明理由.20. 如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为 ,折痕为CE,已知 .
(1)、求点 的坐标;(2)、在坐标平面内是否存在点 ,使得以 、 、 、 为顶点的四边形是等腰梯形?若存在,请直接写出点 的坐标;若不存在,请说明理由.20. 如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为 ,折痕为CE,已知 . (1)、求点 的坐标;(2)、求折痕CE所在直线的解析式;(3)、若点P是y轴上的一个动点,当△CPE为等腰三角形时,请求出点P的坐标.21. 甲、乙两人沿同一路线从学校出发到图书馆,甲先步行出发,6分钟后乙骑自行车出发,乙比甲先到图书馆,甲、乙两人在此过程中以各自的速度匀速运动.甲、乙两人离学校的距离y(米)与甲的行走时间x(分)之间的函数图象如图1所示,甲、乙两人间的距离S(米)与甲的行走时间x(分)之间的函数图象如图2所示.
(1)、求点 的坐标;(2)、求折痕CE所在直线的解析式;(3)、若点P是y轴上的一个动点,当△CPE为等腰三角形时,请求出点P的坐标.21. 甲、乙两人沿同一路线从学校出发到图书馆,甲先步行出发,6分钟后乙骑自行车出发,乙比甲先到图书馆,甲、乙两人在此过程中以各自的速度匀速运动.甲、乙两人离学校的距离y(米)与甲的行走时间x(分)之间的函数图象如图1所示,甲、乙两人间的距离S(米)与甲的行走时间x(分)之间的函数图象如图2所示.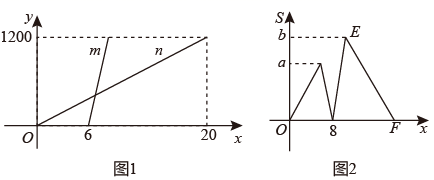 (1)、图1中甲运动的图象是 , 乙运动的图象是 ;(填m、n)(2)、甲的速度为米/分,乙的速度为米/分;(3)、图2中,a= ,b= ;(4)、图2中,求线段EF所在直线的函数解析式.22. 如图1,平面直角坐标系中,直线 交 轴于点 ,交 轴正半轴于点 .
(1)、图1中甲运动的图象是 , 乙运动的图象是 ;(填m、n)(2)、甲的速度为米/分,乙的速度为米/分;(3)、图2中,a= ,b= ;(4)、图2中,求线段EF所在直线的函数解析式.22. 如图1,平面直角坐标系中,直线 交 轴于点 ,交 轴正半轴于点 .

 (1)、求点 的坐标;(2)、如图2,直线 交 轴负半轴于点 ,且 , 为线段 上一点,过点 作 轴的平行线交直线 于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 之间的函数关系式;(3)、在(2)的条件下, 为 延长线上一点,且 ,在线段 上是否存在点 ,使 是以 为斜边的等腰直角三角形,若存在,请求出点 的坐标;若不存在,请说明理由.23. 在平面直角坐标系中,点O为坐标原点,过点B的直线y=﹣ x+ 交x轴于点A,点B的横坐标为1,点C在x轴负半轴,OC=1.
(1)、求点 的坐标;(2)、如图2,直线 交 轴负半轴于点 ,且 , 为线段 上一点,过点 作 轴的平行线交直线 于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 之间的函数关系式;(3)、在(2)的条件下, 为 延长线上一点,且 ,在线段 上是否存在点 ,使 是以 为斜边的等腰直角三角形,若存在,请求出点 的坐标;若不存在,请说明理由.23. 在平面直角坐标系中,点O为坐标原点,过点B的直线y=﹣ x+ 交x轴于点A,点B的横坐标为1,点C在x轴负半轴,OC=1. (1)、如图(1),求直线BC的解析式;(2)、如图(2),点P在直线BC上,点P的横坐标为t,点P在第三象限,过点P作x轴的平行线交直线AB于点Q,设PQ的长为d,求d与t之间的函数关系式,不要求写出自变量t的取值范围;(3)、如图(3),在(2)的条件下,点D在PQ上,CD⊥BC,∠BDA=45°,求d的值.24. 为了“不忘历史,学习英雄”,学校开展“红色丰碑”演讲比赛;王老师负责为获奖同学购买奖品,现甲、乙两个商店正在做促销活动,分别给出了不同的优惠方案:
(1)、如图(1),求直线BC的解析式;(2)、如图(2),点P在直线BC上,点P的横坐标为t,点P在第三象限,过点P作x轴的平行线交直线AB于点Q,设PQ的长为d,求d与t之间的函数关系式,不要求写出自变量t的取值范围;(3)、如图(3),在(2)的条件下,点D在PQ上,CD⊥BC,∠BDA=45°,求d的值.24. 为了“不忘历史,学习英雄”,学校开展“红色丰碑”演讲比赛;王老师负责为获奖同学购买奖品,现甲、乙两个商店正在做促销活动,分别给出了不同的优惠方案:甲商店优惠方案:购买奖品金额超过300元后,超出300元的部分按8折收费;
乙商店优惠方案:购买奖品金额超过500元后,超出500元的部分按a折收费;
如果王老师到乙商店购买奖品,当奖品金额是600元时,实际需支付570元.
(1)、填空:a=.(2)、如果王老师到甲商店购买奖品金额x元,求实际支付y元与奖品金额x元之间的函数表达式.(3)、如果王老师购买奖品的金额超过800元,那么到哪个商店进行采购更合算?