山东省烟台市2020-2021学年高一上学期数学期末考试试卷

试卷更新日期：2021-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. $\sin 17^{°} \cos 13^{°} + \sin 73^{°} \cos 77^{°} =$ （）．

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{1}{2}$ C、 $- \frac{\sqrt{3}}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列函数中，既是其定义域上的单调函数，又是奇函数的是（）．

A、 $y = \tan x$ B、 $y = 3^{x}$ C、 $y = \sqrt{x}$ D、 $y = x^{3}$

查看试题解析
3. 设 $a = \log_{0.3} 3$ ， $b = 2^{- \frac{1}{3}}$ ， $c = \log_{2} 3$ ，则（）．

A、 $c > b > a$ B、 $c > a > b$ C、 $a > c > b$ D、 $b > c > a$

查看试题解析
4. 函数 $f (x) = x^{3} + 3 x - 2$ 的零点所在区间为（）．

A、 $(0 ， \frac{1}{4})$ B、 $(\frac{1}{4} ， \frac{1}{2})$ C、 $(\frac{1}{2} ， \frac{3}{4})$ D、 $(\frac{3}{4} ， 1)$

查看试题解析
5. 已知函数 $y = a^{x + 3} + 3$ （ $a > 0$ ，且 $a \neq 1$ ）的图象恒过点 $P$ ，若角 $α$ 的终边经过点 $P$ ，则 $\cos α =$ （）．

A、 $\frac{3}{5}$ B、 $- \frac{3}{5}$ C、 $\frac{4}{5}$ D、 $- \frac{4}{5}$

查看试题解析
6. 改善农村人居环境，建设美丽宜居乡村，是实施乡村振兴战略的一项重要任务．某地计划将一处废弃的水库改造成水上公园，并绕水库修建一条游览道路．平面示意图如图所示，道路 $O C$ 长度为8（单位：百米）， $O A$ 是函数 $y = \log_{a} (x + b)$ 图象的一部分， $A B C$ 是函数 $y = M \sin (ω x + φ)$ $(M > 0 ， ω > 0 ， | φ | < \frac{π}{2} ， x \in [4 ， 8])$ 的图象，最高点为 $B (5 ， \frac{4 \sqrt{3}}{3})$ ，则道路 $O A B C$ 所对应函数的解析式为（）．

A、 $y = {\begin{array}{l} \log_{\sqrt{3}} (x + 1) ， 0 \leq x < 4 \\ \frac{4 \sqrt{3}}{3} \sin (\frac{π}{6} x - \frac{π}{3}) ， 4 \leq x \leq 8 \end{array}$ B、 $y = {\begin{array}{l} \log_{\sqrt{3}} (x + 1) ， 0 \leq x < 4 \\ \frac{4 \sqrt{3}}{3} \sin (\frac{π}{6} x + \frac{π}{3}) ， 4 \leq x \leq 8 \end{array}$ C、 $y = {\begin{array}{l} \log_{\sqrt{5}} (x + 1) ， 0 \leq x < 4 \\ \frac{4 \sqrt{3}}{3} \sin (\frac{π}{6} x - \frac{π}{3}) ， 4 \leq x \leq 8 \end{array}$ D、 $y = {\begin{array}{l} \log_{\sqrt{5}} (x + 1) ， 0 \leq x < 4 \\ \frac{4 \sqrt{3}}{3} \sin (\frac{π}{6} x + \frac{π}{3}) ， 4 \leq x \leq 8 \end{array}$

查看试题解析
7. 酒驾是严重危害交通安全的违法行为．为了保障交通安全，根据国家有关规定： $100 mL$ 血液中酒精含量达到 $20 ~ 79 mg$ 的驾驶员即为酒后驾车， $80 mg$ 及以上认定为醉酒驾车．假设某驾驶员一天晚上8点喝了一定量的酒后，其血液中的酒精含量上升到 $0.6 mg / m L$ ，如果在停止喝酒后，他血液中酒精含量会以每小时10%的速度减少，则他次日上午最早几点（结果取整数）开车才不构成酒后驾车？（参考数据： $\lg 3 \approx 0.477$ ）（）．

A、6 B、7 C、8 D、9

查看试题解析
8. 将函数 $f (x) = \cos (2 x - \frac{π}{3})$ 的图象向左平移 $φ (0 < φ < \frac{π}{2})$ 个单位长度得到函数 $g (x)$ 的图象，若 $x_{1}$ ， $x_{2}$ 使得 $f (x_{1}) g (x_{2}) = - 1$ ，且 $| x_{1} - x_{2} |$ 的最小值为 $\frac{π}{6}$ ，则 $φ =$ （）．

A、 $\frac{π}{12}$ B、 $\frac{π}{6}$ C、 $\frac{π}{4}$ D、 $\frac{π}{3}$

查看试题解析

二、多选题

9. 下列说法正确的有（）．

A、经过30分钟，钟表的分针转过 $- 2 π$ 弧度 B、若 $\sin θ > 0$ ， $\cos θ < 0$ ，则 $θ$ 为第二象限角 C、若 $\sin θ + \cos θ > 1$ ，则 $θ$ 为第一象限角 D、函数 $y = \sin | x |$ 是周期为 $π$ 的偶函数

查看试题解析
10. 已知函数 $f (x) = \sin x + \cos x$ ，则（）．

A、 $f (x)$ 在 $(\frac{π}{2} ， π)$ 上单调递减 B、 $f (x)$ 图象关于点 $（ \frac{3}{4} π ， 0 ）$ 对称 C、 $f (x)$ 图象的两条相邻对称轴之间的距离为 $π$ D、当 $x = \frac{π}{4} + 2 k π (k \in Z)$ 时， $f (x)$ 取得最小值

查看试题解析
11. 已知函数 $f (x) = \log_{a} x + \log_{a} (a - x)$ （ $a > 0$ ，且 $a \neq 1$ ），则（）．

A、 $f (x)$ 定义域为 $(0 ， a)$ B、 $f (x)$ 的最大值为 $2 - 2 \log_{a} 2$ C、若 $f (x)$ 在 $(0 ， 2)$ 上单调递增，则 $1 < a \leq 4$ D、 $f (x)$ 图象关于直线 $x = \frac{a}{2}$ 对称

查看试题解析
12. 定义新运算“ $\otimes$ ”： $x \otimes y = \log_{2} (2^{x} + 2^{y})$ ， $x ， y \in R$ ，则对任意实数 $a$ ， $b$ ， $c$ 有（）．

A、 $a \otimes a = 2 a$ B、 $(a \otimes b) \otimes c = a \otimes (b \otimes c)$ C、 $a \otimes b \geq 1 + \frac{a + b}{2}$ D、 $(a \otimes b) - c = (a - c) \otimes (b - c)$

查看试题解析

三、填空题

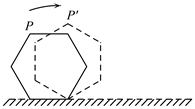
13. 已知函数 $f (x) = x^{2} - 2 x - a$ 有两个不同的零点，则实数a的取值范围是．

查看试题解析
14. 若幂函数 $f (x) = (m^{2} - m - 1) x^{m^{2} + 2 m}$ 的图象不经过原点，则实数 $m$ 的值为．

查看试题解析
15. 函数 $y = \sqrt{\sin x + \frac{1}{2}}$ 的定义域为．

查看试题解析
16. 如图，边长为1的正六边形木块自图中实线标记位置起在水平桌面上从左向右做无滑动翻滚，点 $P$ 为正六边形的一个顶点，当点 $P$ 第一次落在桌面上时，点 $P$ 走过的路程为．

查看试题解析

四、解答题

17. 化简求值：

(1)、 ${(\frac{27}{8})}^{- \frac{2}{3}} + π^{0} + \log_{2} \frac{2}{3} - \log_{4} \frac{16}{9}$ ；

(2)、已知 $\tan α = - 2$ ，求 $\frac{2 \sin (π - α) + \sin (\frac{π}{2} + α)}{\cos (- α) + \sin (α - 3 π)}$ 的值．

查看试题解析
18. 在① $f (x)$ 图象过点 $(\frac{π}{2} ， 1)$ ，② $f (x)$ 图象关于直线 $x = \frac{2 π}{3}$ 对称，③ $f (x)$ 图象关于点 $(\frac{π}{6} ， 0)$ 对称，这三个条件中任选一个，补充在下面问题中，并给出解答．
问题：已知 $f (x) = 2 \sin (ω x + φ) (ω > 0 ， - \frac{π}{2} < φ < 0)$ 的最小正周期为 $2 π$ ，________．

(1)、求函数 $f (x)$ 的解析式；

(2)、将 $f (x)$ 的图象上所有点向左平移 $\frac{π}{12}$ 个单位长度，再将得到的图象上每个点的横坐标缩短到原来的 $\frac{1}{2}$ （纵坐标不变），得到函数 $y = g (x)$ 的图象，求 $g (x)$ 的单调递增区间．

查看试题解析
19.

(1)、求函数 $= {(\log_{2} x)}^{2} + \log_{2} x$ ， $x \in [\frac{1}{2} ， 2]$ 的值域；

(2)、解关于 $x$ 的不等式： $\log_{a} (x + 1) > \log_{a} (3 - x^{2})$ （ $a > 0$ ，且 $a \neq 1$ ）．

查看试题解析
20. 已知函数 $f (x) = 2 \cos (x - \frac{π}{3}) \cos x + 1$ ．

(1)、设 $x \in [- \frac{π}{6} ， \frac{π}{3}]$ ，求 $f (x)$ 的最值及相应 $x$ 的值；

(2)、设 $f (α + \frac{π}{12}) = \frac{11}{6}$ ，求 $\cos (\frac{7 π}{6} - 2 α)$ 的值．

查看试题解析
21. 为提升居民生活质量，增加城市活力，某市决定充分利用城市空间修建口袋公园．如图所示，现有一处边长为 $40 m$ 的正方形空地 $A B C D$ ，若已规划出以 $A$ 为圆心、半径为 $30 m$ 的扇形健身场地 $A E F$ ，欲在剩余部修建一块矩形草坪 $P M C N$ ，其中点 $P$ 在圆弧 $E F$ 上，点 $M$ ， $N$ 分别落在 $B C$ 和 $C D$ 上，设 $∠ P A B = θ$ ，矩形草坪 $P M C N$ 的面积为 $S$ ．

(1)、求 $S$ 关于 $θ$ 的函数关系式；

(2)、求 $S$ 的最大值以及相应 $θ$ 的值．

查看试题解析
22. 已知 $f (x)$ 为 $R$ 上的奇函数， $g (x)$ 为 $R$ 上的偶函数，且 $f (x) + g (x) = 2 e^{x}$ ，其中 $e = 2.71828$ …．

(1)、求函数 $f (x)$ 和 $g (x)$ 的解析式；

(2)、若不等式 $f (x^{2} + 3) + f (1 - a x) > 0$ 在 $(0 ， + \infty)$ 恒成立，求实数 $a$ 的取值范围；

(3)、若 $\forall x_{1} \in [0 ， 1]$ ， $\exists x_{2} \in [m ， + \infty)$ ，使 $f (x_{2}) = e^{- | x_{1} - m |}$ 成立，求实数 $m$ 的取值范围．

查看试题解析