辽宁省辽阳市2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-11-10 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 已知 ,则( )A、 B、 C、 D、4. “ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 函数 的图象大致为A、
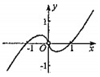 B、
B、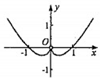 C、
C、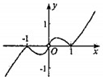 D、
D、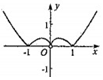 6. 某商场开通三种平台销售商品,五一期间这三种平台的数据如图1所示.该商场为了解消费者对各平台销售方式的满意程度,用分层抽样的方法抽取了6%的顾客进行满意度调查,得到的数据如图2所示.下列说法正确的是( )
6. 某商场开通三种平台销售商品,五一期间这三种平台的数据如图1所示.该商场为了解消费者对各平台销售方式的满意程度,用分层抽样的方法抽取了6%的顾客进行满意度调查,得到的数据如图2所示.下列说法正确的是( ) A、总体中对平台一满意的消费人数约为36 B、样本中对平台二满意的消费人数为300 C、若样本中对平台三满意的消费人数为120,则 D、样本中对平台一和平台二满意的消费总人数为547. 下表为随机数表的一部分:
A、总体中对平台一满意的消费人数约为36 B、样本中对平台二满意的消费人数为300 C、若样本中对平台三满意的消费人数为120,则 D、样本中对平台一和平台二满意的消费总人数为547. 下表为随机数表的一部分:08015 17727 45318 22374 21115 78253
77214 77402 43236 00210 45521 64237
已知甲班有60位同学,编号为 号,规定:利用上面的随机数表,从第1行第4列的数开始,从左向右依次读取2个数,则抽到的第8位同学的编号是( )
A、11 B、15 C、25 D、378. 已知 表示实数 , , 中的最小值,设函数 ,若 的最大值为4,则 的解析式可以为( )A、 B、 C、 D、二、多选题
-
9. 若向量 与 共线,则( )A、 B、 C、 D、10. 已知函数 在其定义域内单调递增,且 ,若 的反函数为 ,则( )A、 B、 在定义域内单调递增 C、 D、 在定义域内单调递减11. 若幂函数 在 上单调递增,则( )A、 B、 C、 D、12. 设非零实数 , 满足 ,则( )A、 B、 C、 D、
三、填空题
-
13. 已知 ,则 的最小值为 , 此时 .14. 已知 , ,且C与A关于点B对称,则C的坐标为 .15. 已知一组样本数据1、2、 、8的极差为8,若 ,则其方差为 .16. 已知函数 若方程 有6个不同的实数解,则m的取值范围是 .
四、解答题
-
17. 在① ,②函数 的图象经过点 ,③ , 这三个条件中任选一个,补充在下面的问题中并解答.
问题:已知集合 , ,且 ▲ , 求 .
18.(1)、设 , 是两个不共线的向量, , , ,证明:A,B,D三点共线.(2)、已知E,F分别是 边AB,AC上的点,且 , .如果 , ,试用向量 , 表示 , .19. 已知函数 .(1)、求函数 的单调区间;(2)、求不等式 的解集.20. 甲、乙两人想参加某项竞赛,根据以往20次的测试,将样本数据分成 , , , 五组,并整理得到如下频率分布直方图:

已知甲测试成绩的中位数为75.
(1)、求x,y的值,并求出甲的测试成绩的平均数(假设同一组中的每个数据可用该组区间中点值代替);(2)、从甲、乙两人测试成绩不足60分的试卷中随机抽取3份,求恰有2份来自乙的概率.