江西省景德镇市2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-11-10 类型:期末考试
一、单选题
-
1. 直线 的倾斜角为( )A、30º B、60º C、120º D、150º2. m,n为空间中两条不重合直线, 为空间中一平面,则下列说法正确的是( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则3. 已知集合 , ,则 ( )A、 B、 C、 D、4. 已知三点 , , 在同一条直线上,则实数 的值为( )A、0 B、5 C、0或5 D、0或-55. 在平面四边形 中, ,将该四边形沿着对角线 折叠,得到空间四边形 ,则异面直线 所成的角是( )A、 B、 C、 D、6. 直线 与直线 的交点在第四象限,则实数 的取值范围为( )A、 B、 C、 D、7. 已知函数 ,记 , , ,则 , , 的大小关系为( )A、 B、 C、 D、8. 如图,圆锥的母线长为4,点M为母线AB的中点,从点M处拉一条绳子,绕圆锥的侧面转一周达到B点,这条绳子的长度最短值为 ,则此圆锥的表面积为( )
 A、4π B、5π C、6π D、8π9. 如图,在各小正方形边长为1的网格上依次为某几何体的正视图,侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为 ( )
A、4π B、5π C、6π D、8π9. 如图,在各小正方形边长为1的网格上依次为某几何体的正视图,侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为 ( ) A、 B、 C、 D、10. 如图,点P在正方体 的面对角线 上运动,则下列四个结论:
A、 B、 C、 D、10. 如图,点P在正方体 的面对角线 上运动,则下列四个结论: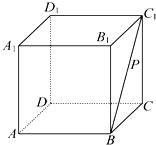
三棱锥 的体积不变;
平面 ;
;
平面 平面 .
其中正确的结论的个数是
A、1个 B、2个 C、3个 D、4个11. 攒尖是古代中国建筑中屋顶的一种结构形式.依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖.也有单檐和重檐之分.多见于亭阁式建筑,园林建筑.以八中校园腾龙阁为例,它属重檐四角攒尖,它的上层轮廓可近似看作一个正四棱锥,若此正四棱锥的侧面积是底面积的3倍,则此正四棱锥的内切球半径与底面边长比为( ) A、 B、 C、 D、12. 设函数 ,若函数 在区间 内有且仅有一个零点,则实数t的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、12. 设函数 ,若函数 在区间 内有且仅有一个零点,则实数t的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 如图所示, 为水平放置的 的直观图,其中 , ,则 的面积是.
 14. 已知正四棱锥的底面边长为2,现用一平行于正四棱锥底面的平面去截这个棱锥,截得棱台的上、下底面的面积之比为1:4,若截去的小棱锥的侧棱长为2,则此棱台的表面积为.15. 经过点 ,且在坐标轴上截距相等的直线方程为.16. 函数 在区间 上为单调递减函数,则实数 的取值范围为.
14. 已知正四棱锥的底面边长为2,现用一平行于正四棱锥底面的平面去截这个棱锥,截得棱台的上、下底面的面积之比为1:4,若截去的小棱锥的侧棱长为2,则此棱台的表面积为.15. 经过点 ,且在坐标轴上截距相等的直线方程为.16. 函数 在区间 上为单调递减函数,则实数 的取值范围为.三、解答题
-
17. 已知直线 : 和 : ,分别就下列条件求出实数m的值.(1)、直线 与 垂直;(2)、直线 与 平行.18. 如图,长方体 由, , , ,过 作长方体的截面 使它成为正方形.
 (1)、求三棱柱 的外接球的表面积;(2)、求 .19. 已知直线 : , : .(1)、求直线 过的定点P,并求出直线 的方程,使得定点P到直线 的距离为 ;(2)、过点P引直线 分别交 , 轴正半轴于A、B两点,求使得 面积最小时,直线 的方程.
(1)、求三棱柱 的外接球的表面积;(2)、求 .19. 已知直线 : , : .(1)、求直线 过的定点P,并求出直线 的方程,使得定点P到直线 的距离为 ;(2)、过点P引直线 分别交 , 轴正半轴于A、B两点,求使得 面积最小时,直线 的方程.

