吉林省白城市通榆县2021-2022学年第一学期九年级数学第二次月考试题
试卷更新日期:2021-11-09 类型:月考试卷
一、单项选择题
-
1. 二次函数y=(x-2)2+1的图像的顶点坐标是( )A、(2,1) B、(-2,1) C、(2,-1) D、(-2,-1)2. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用配方法解关于x的一元二次方程x2-8x+5=0,将其化成(x+a)2=b的形式,则变形正确的是( )A、(x+4)2=21 B、(x-4)2=21 C、(x+4)2=11 D、(x-4)2=114. 已知函数y=-x2+bx+c,其中b>0,c<0,此函数的图象可能是( )A、
3. 用配方法解关于x的一元二次方程x2-8x+5=0,将其化成(x+a)2=b的形式,则变形正确的是( )A、(x+4)2=21 B、(x-4)2=21 C、(x+4)2=11 D、(x-4)2=114. 已知函数y=-x2+bx+c,其中b>0,c<0,此函数的图象可能是( )A、 B、
B、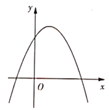 C、
C、 D、
D、 5. 如图,在 中,半径 ,点 是优弧 上的一点,点 是 的中点,连接 , ,则 的度数为( )
5. 如图,在 中,半径 ,点 是优弧 上的一点,点 是 的中点,连接 , ,则 的度数为( ) A、20° B、22.5° C、25° D、45°6. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',当点C'落在边AB上时,线段CC'的长为( )
A、20° B、22.5° C、25° D、45°6. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',当点C'落在边AB上时,线段CC'的长为( )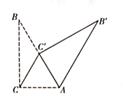 A、 B、1 C、 D、2
A、 B、1 C、 D、2二、填空题
-
7. 一元二次方程x(x+1)=0的两根分别为8. 若关于x的方程x2+6x+m=0有两个不相等的实数根,则实数m的取值范围是9. 二次函数y=(x-1)2-4的最小值是10. 沿着x轴正方向看,抛物线y=x2-2在y轴左侧的部分是的(填“上升”或“下降”)11. 如图,在⊙O中,弦AB=16,C为弦AB的中点,⊙O的半径长为10,则线段OC的长为
 12. 如图,四边形ABCD内接于⊙O,连接BD, = ,∠BDC=40°,则∠ADC的度数是
12. 如图,四边形ABCD内接于⊙O,连接BD, = ,∠BDC=40°,则∠ADC的度数是 13. 如图,将△ABC绕点A逆时针旋转到△AED,其中点B与点E是对应点,点C与点D是对应点,且DC∥AB,若∠CAB=65°,则∠CAE的度数为
13. 如图,将△ABC绕点A逆时针旋转到△AED,其中点B与点E是对应点,点C与点D是对应点,且DC∥AB,若∠CAB=65°,则∠CAE的度数为 14. 如图,单孔拱桥的形状近似抛物线形,建立如图所示的平而直角坐标系,在正常水位时,水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m,则抛物线的解析式为
14. 如图,单孔拱桥的形状近似抛物线形,建立如图所示的平而直角坐标系,在正常水位时,水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m,则抛物线的解析式为
三、解答题
-
15. 解方程:x2-4x+1=016. 如图,△ABC是等边三角形,点D在线段BC上,连接AD , 将线段AD绕点A逆时针旋转60°得到线段AE , 连接CE . 求证: .
 17. 某旅游团旅游结束时,其中一名旅客建议大家互相握手道别,细心的小明发现,每两个参加旅游的人互握一次手,共握了66次,问这次旅游的旅客人数是多少?18. 已知点A(a,7)在抛物线y=x2+4x+10上.(1)、求点A的坐标.(2)、求抛物线的对称轴和顶点坐标.
17. 某旅游团旅游结束时,其中一名旅客建议大家互相握手道别,细心的小明发现,每两个参加旅游的人互握一次手,共握了66次,问这次旅游的旅客人数是多少?18. 已知点A(a,7)在抛物线y=x2+4x+10上.(1)、求点A的坐标.(2)、求抛物线的对称轴和顶点坐标.四、解答题
-
19. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,0),B(-4,1),C(-2,2).

⑴点B关于原点对称的点B'的坐标为 ▲ .
⑵平移△ABC,使平移后点A的对应点A1的坐标为(2,1),请画出平移后的△A1B1C1 .
⑶画出△ABC绕原点O逆时针旋转90'后得到的△A2B2C2
20. 如图,四边形ABCD是⊙O的内接四边形,∠BAC=60°,∠DAC=30°,AB=2,AD=6.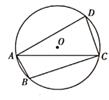 (1)、求∠DCB的度数.(2)、求CD的长.21. 如图,在等腰三角形ABC中,BA=BC,∠ABC=α.作AD⊥BC于点D,将线段BD绕点B顺时针旋转角a后得到线段BE,连接CE.
(1)、求∠DCB的度数.(2)、求CD的长.21. 如图,在等腰三角形ABC中,BA=BC,∠ABC=α.作AD⊥BC于点D,将线段BD绕点B顺时针旋转角a后得到线段BE,连接CE. (1)、求证:BE⊥CE.(2)、延长线段AD,交线段CE于点F,直接写出∠CFA的度数.(用含α的式子表示)22. 如图是某个二次函数的部分图像。
(1)、求证:BE⊥CE.(2)、延长线段AD,交线段CE于点F,直接写出∠CFA的度数.(用含α的式子表示)22. 如图是某个二次函数的部分图像。 (1)、求该二次函数的解析式。(2)、补全函数图象。(3)、若抛物线上点P(m,n)到y轴的距离不大于2,请根据图像直接写出n的取值范围。
(1)、求该二次函数的解析式。(2)、补全函数图象。(3)、若抛物线上点P(m,n)到y轴的距离不大于2,请根据图像直接写出n的取值范围。五、解答题
-
23. 如图,在矩形ABCD中,点O为边AB上一点,以点O为圆心,OA为半径的⊙O与对角线AC相交于点E,连接BE,当BE为⊙O的切线时,解答下列问题.
 (1)、求证:BC=BE.(2)、若点E为AC的中点,⊙O的半径为1,求矩形ABCD的面积。24. 如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为工米,草坪面积为y平方米.
(1)、求证:BC=BE.(2)、若点E为AC的中点,⊙O的半径为1,求矩形ABCD的面积。24. 如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为工米,草坪面积为y平方米. (1)、请直接写出y关于x的函数解析式.(不必写出x的取值范围)(2)、若草坪的面积为120平方米,请求出竖甬道的宽度.
(1)、请直接写出y关于x的函数解析式.(不必写出x的取值范围)(2)、若草坪的面积为120平方米,请求出竖甬道的宽度.六、解答题
-
25. 如图①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC,将△DEC绕点C顺时针旋转。
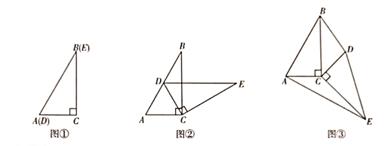 (1)、当ODEC绕点C旋转到点D恰好落在AB边上时,如图②.
(1)、当ODEC绕点C旋转到点D恰好落在AB边上时,如图②.①当∠B=∠E=30°时,此时旋转角的大小为 ▲ ,
②当∠B=∠E=α时,求此时旋转角的大小.(用含α的式子表示)
(2)、当△DEC绕点C旋转到如图③所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确.若正确,请你证明小杨同学的猜想:若不正确,请说明理由。26. 在平面直角坐标系中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C. (1)、点A的坐标为(2)、当S△ABC=15时,求该抛物线的解析式.(3)、在(2)的条件下,若经过点C的直线l:y=kx+b(k<0)与抛物线的另一个交点为D,该抛物线在直线l上方的部分与线段CD组成一个新函数的图象.请结合图像回答:若新函数的最小值大于-8,直接写出k的取值范围。
(1)、点A的坐标为(2)、当S△ABC=15时,求该抛物线的解析式.(3)、在(2)的条件下,若经过点C的直线l:y=kx+b(k<0)与抛物线的另一个交点为D,该抛物线在直线l上方的部分与线段CD组成一个新函数的图象.请结合图像回答:若新函数的最小值大于-8,直接写出k的取值范围。