山东省淄博市周村区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下面四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若分式 有意义,则实数x的取值范围是( )A、 B、 C、 D、3. 下列多项式能用完全平方公式进行因式分解的是( )A、a2﹣1 B、a2+4 C、a2+2a+1 D、a2﹣4a﹣44. 如图,在平行四边形ABCD中,点E , F分别在AD和BC上,下列条件不能判定四边形AECF是平行四边形的为( )
2. 若分式 有意义,则实数x的取值范围是( )A、 B、 C、 D、3. 下列多项式能用完全平方公式进行因式分解的是( )A、a2﹣1 B、a2+4 C、a2+2a+1 D、a2﹣4a﹣44. 如图,在平行四边形ABCD中,点E , F分别在AD和BC上,下列条件不能判定四边形AECF是平行四边形的为( ) A、AF=CE B、DE=BF C、AF∥CE D、∠AFB=∠DEC5. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作▱AEDF.在点E从点B移动到点C的过程中,▱AEDF的面积( )
A、AF=CE B、DE=BF C、AF∥CE D、∠AFB=∠DEC5. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作▱AEDF.在点E从点B移动到点C的过程中,▱AEDF的面积( ) A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变6. 如图, 绕点 按逆时针方向旋转56°后与 重合,则 ( )
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变6. 如图, 绕点 按逆时针方向旋转56°后与 重合,则 ( ) A、58° B、56° C、62° D、68°7. “按情就是命令,防控就是责任!”在去年新冠肺炎疫情爆发期间,我区教师发扬不畏艰险、无私奉献的精神,挺身而出,协助社区做好疫情监测、排查、防控等工作.现将50名教师参加社区工作时间 (单位:天)的情况统计如下:
A、58° B、56° C、62° D、68°7. “按情就是命令,防控就是责任!”在去年新冠肺炎疫情爆发期间,我区教师发扬不畏艰险、无私奉献的精神,挺身而出,协助社区做好疫情监测、排查、防控等工作.现将50名教师参加社区工作时间 (单位:天)的情况统计如下:时间 (天)
15
25
35
45
教师人数
4
6
7
13
20
下面是对这50名教师参加社区工作时间的推断:
①平均数一定在40~50之间;②平均数可能在40~50之间;③中位数一定是45;④众数一定是50.其中正确的推断是( )
A、①④ B、②③ C、③④ D、②③④8. 已知一组数据的方差 ,则 的值为( )A、22 B、21 C、20 D、79. 如图,菱形 的边 的垂直平分线交 于点 ,交 于点 ,连接 .当 时,则 ( )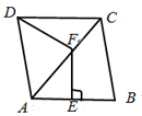 A、15° B、30° C、40° D、50°10. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( )
A、15° B、30° C、40° D、50°10. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、11. 如图,正方形 的对角线相交于点 ,正方形 与 的边长均为 , 与 相交于点 , 与 相交于点 ,且满足 ,则两个正方形重合部分的面积为( )
A、 B、 C、 D、11. 如图,正方形 的对角线相交于点 ,正方形 与 的边长均为 , 与 相交于点 , 与 相交于点 ,且满足 ,则两个正方形重合部分的面积为( ) A、 B、 C、 D、12. 如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A、 B、 C、 D、12. 如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )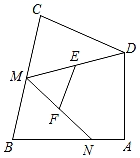 A、8 B、7 C、6 D、5
A、8 B、7 C、6 D、5二、填空题
-
13. 分解因式: .14. 五边形 的内角和是度.15. 在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .16. 如图, 是 的对角线,点 在 上, , ,则 的度数是 .
 17. 如图,在菱形 中, , ,点 是直线 , 之间任意一点,连接 , , , ,则 和 的面积之和是 .
17. 如图,在菱形 中, , ,点 是直线 , 之间任意一点,连接 , , , ,则 和 的面积之和是 . 18. 如图,有一张长方形片ABCD, , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
18. 如图,有一张长方形片ABCD, , .点E为CD上一点,将纸片沿AE折叠,BC的对应边 恰好经过点D,则线段DE的长为cm.
三、解答题
-
19. 分解因式:(1)、 ;(2)、 .20. 如图, 中, , , ,先将 绕着点 顺时针旋转90°,再向上平移2个单位得到 .
 (1)、请在给定的坐标系中画出 ;(2)、 可以看作是由 顺时针旋转一次而来,请直接写出旋转中心的坐标和旋转角的度数.21. 分式计算与解方程:(1)、 ;(2)、 .22. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作 , ,垂足分别为E,F.AC平分 .
(1)、请在给定的坐标系中画出 ;(2)、 可以看作是由 顺时针旋转一次而来,请直接写出旋转中心的坐标和旋转角的度数.21. 分式计算与解方程:(1)、 ;(2)、 .22. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作 , ,垂足分别为E,F.AC平分 .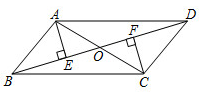 (1)、若 ,求 的度数;(2)、求证: .23. 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)、若 ,求 的度数;(2)、求证: .23. 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.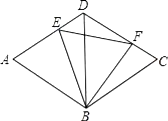 (1)、求证:△BDE≌△BCF;(2)、判断△BEF的形状,并说明理由.
(1)、求证:△BDE≌△BCF;(2)、判断△BEF的形状,并说明理由.
24. 随着智能分拣设备在快递业务中的普及,快件分拣效率大幅提高.使用某品牌智能分拣设备,每人每小时分拣的快件量是传统分拣方式的25倍,经过测试,由5人用此设备分拣8000件快件的时间,比20人用传统方式分拣同样数量的快件节省4小时.(1)、使用智能分拣设备后,每人每小时可分拣快件多少件?(2)、已知某快递中转站平均每天需要分拣10万件快件,每天工作时间为8小时,如果使用此智能分拣设备,每天只需要安排多少名工人就可以完成分拣工作?


