山东省淄博市张店区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{3}{x + 1}$ 无意义，则（）．

A、 $x = - 2$ B、 $x = - 1$ C、 $x = 1$ D、 $x = 2$

查看试题解析
2. 垃圾分类制度陆续在淄博市各地区实施．下列图标分别表示可回收垃圾，厨余垃圾，有害垃圾，其他垃圾四种垃圾回收标识中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 计算 ${(- 2)}^{2020} + {(- 2)}^{2021}$ 所得的结果是（）．

A、 $- 2^{2020}$ B、 $- 2^{2021}$ C、 $2^{2020}$ D、-2

查看试题解析
4. 下列多项式：① $x^{2} + y^{2}$ ；② $- x^{2} - 4 y^{2}$ ；③ $- 1 + a^{2}$ ；④ $b^{2} - a^{2}$ ，其中能用平方差公式分解因式的多项式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 化简 $(\frac{1}{x - 3} - \frac{x + 1}{x^{2} - 1}) \div \frac{1}{x - 3}$ 的结果是（）

A、2 B、 $\frac{2}{x - 3}$ C、 $\frac{x - 4}{x - 1}$ D、 $\frac{2}{x - 1}$

查看试题解析
6. 内角和为720°的多边形是（）．

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
7. 甲，乙，丙，丁四位同学本学期5次50米短跑成绩的平均数 $\bar{x}$ （秒）及方差 $S^{2}$ 如下表所示．若从这四位同学中选出一位成绩较好且状态稳定的同学参加学校比赛，则应该选的同学是（）

甲

乙

丙

丁

$\bar{x}$

7

7

7.5

7.5

$S^{2}$

0.45

0.2

0.2

0.45

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图，四边形ABCD的对角线AC，BD相交于点O，下列条件不能判定四边形ABCD是平行四边行的是（）

A、OA＝OC，OB＝OD B、AB＝CD，AD＝BC C、AB∥CD，AD＝BC D、∠ABD＝∠CDB，∠ADB＝∠CBD

查看试题解析
9. 如图，在平面直角坐标系中，△ABC的顶点都在方格线的格点上，将△ABC绕点P顺时针方向旋转90°，得到△A'B'C'，则点P的坐标为（）

A、(0，4) B、(1，1) C、(1，2) D、(2，1)

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中， $D E$ 平分 $∠ A D C$ ， $A D = 6$ ， $B E = 2$ ，则平行四边形ABCD的周长是（）

A、16 B、14 C、20 D、24

查看试题解析
11. 如图，将 $△ A B C$ 绕点B按逆时针方向旋转 $40^{\circ}$ 到 $△ D B E$ （其中点D与点A对应，点E与点C对应），连接 $A D$ ，若 $A D$ // $B C$ ，则 $∠ A B E$ 的度数为（）

A、 $25^{\circ}$ B、 $30^{\circ}$ C、 $35^{\circ}$ D、 $40^{\circ}$

查看试题解析
12. 如图，点 $E$ 、 $F$ 分别在正方形 $A B C D$ 的边 $B C$ 、 $C D$ 上， $∠ E A F = 45 °$ ，已知 $A D = 6$ （正方形的四条边都相等，四个内角都是直角）， $D F = 2$ ．则 $△ A E F$ 的面积 $S_{△ A E F} =$ （）

A、6 B、12 C、15 D、30

查看试题解析

二、填空题

13. 如图，五边形 $A B C D E$ 的外角和为度．

查看试题解析
14. 请写出一个你认为能够镶嵌平面的正多边形组合：和．

查看试题解析
15. 如图，□ $A B C D$ 中， $F ， E$ 分别在边 $A D ， B C$ 上，要使 $A E = C F$ ，需要添加的条件是（只填一个你认为正确的即可）．

查看试题解析
16. 已知关于 $x$ 的分式方程 $\frac{x}{x - 1} - 3 = \frac{k}{x - 1}$ 无解，则 $k =$ ．

查看试题解析
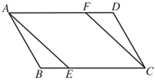17. 如图，①是一个周长为6的三角形，分别连接这个三角形三边中点得到第一个新的三角形，其周长为 $l_{1}$ ，如图②，再连接图②中第一个新的三角形三边的中点得到第二个新的三角形，其周长为 $l_{2}$ ，如图③，…，按这样的方法进行下去，第 $n$ 个新的三角形的周长 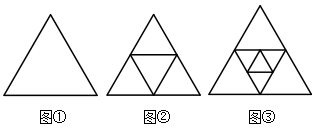$l_{n} =$ ．

查看试题解析

三、解答题

18. 计算．

(1)、因式分解： $x^{2} y + 4 x y + 3 y$ ．

(2)、解方程： $\frac{2}{x - 2} - \frac{3}{x^{2} - 4 x + 4} = \frac{1}{2 - x}$ ．

查看试题解析
19. 如图，四边形ABCD是平行四边形，E是BC边上一点，只用一把无刻度的直尺在AD边上作点F，使得DF=BE．

(1)、作出满足题意的点F，简要说明你的作图过程；

(2)、依据你的作图，证明：DF=BE．

查看试题解析

20. 某学校组织了一次知识竞赛，每班选25名同学参加比赛，成绩分别为

A

、

B

、

C

、

D

四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成统计图，如图所示．

一班竞赛成绩统计图二班竞赛成绩统计图

根据以上提供的信息解答下列问题：

(1)、计算后，在图中用虚线画出二班竞赛成绩的频数分布折线统计图．

(2)、直接写出下表中

a

、

b

、

c

的值：

	平均数（分）	中位数（分）	众数（分）
一班	$a$	$b$	90
二班	87.6	80	$c$

(3)、请从以下给出的三个方面分别对一班和二班这次竞赛成绩的结果进行分析：

①从平均数和中位数方面比较一班和二班的成绩．

②从平均数和众数方面比较一班和二班的成绩．

③从 $B$ 级以上（包括 $B$ 级）的人数方面来比较一班和二班的成绩．

查看试题解析

21. 如图，平面直角坐标系的原点在边长为1个单位长度的小正方形组成的网格的格点上， $△ A B C$ 为格点三角形（三角形的顶点在网格的格点上）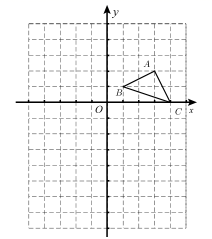

(1)、直接写出下列点的坐标： $A$ （，）， $B$ （，）， $C$ （，）．

(2)、直接画出经过下列变换后的图形：将 $△ A B C$ 向右平移1个单位，再向下平移6个单位后，得到 $△ A_{1} B_{1} C_{1}$ （其中：点 $A$ 移动后为点 $A_{1}$ ，点 $B$ 移动后为点 $B_{1}$ ，点 $C$ 移动后为点 $C_{1}$ ）再将其绕点 $A_{1}$ 顺时针旋转180°得到 $△ A_{2} B_{2} C_{2}$ ．

(3)、通过观察分析判断 $△ A B C$ 与 $△ A_{2} B_{2} C_{2}$ 是否关于某点成中心对称？如果是，直接写出对称中心的坐标；如果不是，说明理由．

查看试题解析
22. 新型冠状病毒肺炎疫情发生后，全社会积极参与疫情防控工作，某市为了尽快完成200万只医用外科口罩的生产任务，安排甲、乙两个大型工厂完成．已知甲厂每天生产口罩的数量是乙厂每天生产口罩数量的2倍，并且在独立完成60万只口罩的生产任务时，甲厂比乙厂少用5天．问甲、乙两厂每天各生产多少万只口罩？

查看试题解析
23. 如图1，在 $△ A B C$ 中，点 $D$ 是边 $B C$ 的中点，点 $E$ 在 $△ A B C$ 内， $A E$ 平分 $∠ B A C$ ， $C E ⊥ A E$ ，点 $F$ 在边 $A B$ 上， $E F // B C$ ．

(1)、求证：四边形 $B D E F$ 是平行四边形．

(2)、判断线段 $B F$ 、 $A B$ 、 $A C$ 的数量之间具有怎样的关系？证明你所得到的结论．

(3)、点 $P$ 是 $△ A B C$ 的边 $A B$ 上的一点，若 $△ D C E$ 的面积 $S_{△ D C E} = 3$ ，请直接写出 $△ D P E$ 的面积（不需要写出解答过程）．

查看试题解析
24. （探究）：

(1)、在图1中，已知线段 $A B$ 、 $C D$ ，其两条线段的中点分别为 $E$ 、 $F$ ，请填写下面空格．
①若 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，则 $E$ 点坐标为．

②若 $C (- 2 ， 2)$ ， $D (- 2 ， - 1)$ ，则 $F$ 点坐标为．

(2)、请回答下列问题
①在图2中，已知线段 $A B$ 的端点坐标为 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，求出图中线段 $A B$ 的中点 $P$ 的坐标（用含 $x_{1}$ ， $y_{1}$ ， $x_{2}$ ， $y_{2}$ 的代数式表示），并给出求解过程．

②（归纳）：无论线段 $A B$ 处于直角坐标系中的哪个位置，当其端点坐标为 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，线段 $A B$ 的中点为 $P (x ， y)$ 时， $x$ = ▲ ， $y$ = ▲ ．（直接填写，不必证明）

③（运用）：在图3中，在平面直角坐标系中 $△ A O B$ 的三个顶点 $O (0 ， 0)$ ， $A (- 2 ， 3)$ ， $B (4 ， 1)$ ，若以 $A$ ， $O$ ， $B$ ， $M$ 为顶点的四边形是平行四边形，请利用上面的结论直接写出顶点 $M$ 的坐标（不需写出解答过程）

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	7	7	7.5	7.5
$S^{2}$	0.45	0.2	0.2	0.45