山东省淄博市临淄区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列多项式中,能运用平方差公式分解因式的是( )A、 B、 C、 D、2. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解3. 若 ,则下列分式化简正确的是( )A、 B、 C、 D、4. 若关于x的分式方程 = +5的解为正数,则m的取值范围为( )A、m<﹣10 B、m≤﹣10 C、m≥﹣10且m≠﹣6 D、m>﹣10且m≠﹣65. 冉冉的妈妈在网上销售装饰品.最近一周, 每天销售某种装饰品的个数为:.11,10,11,13,11,13,15关于这组数据,冉冉得出如下结果,其中错误的是( )A、众数是11 B、平均数是12 C、方差是 D、中位数是136. 小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,并将调查结果绘制成折线统计图(如图),则下列说法正确的是( )
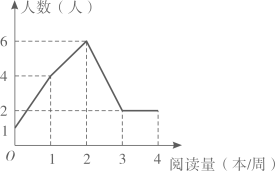 A、中位数是3,众数是2 B、众数是1,平均数是2 C、中位数是2,众数是2 D、中位数是3,平均数是2.57. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形8. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )
A、中位数是3,众数是2 B、众数是1,平均数是2 C、中位数是2,众数是2 D、中位数是3,平均数是2.57. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形8. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )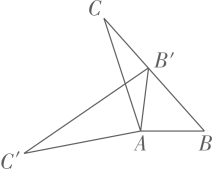 A、 B、 C、 D、9. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )
A、 B、 C、 D、9. 在下图的四个三角形中,不能由 经过旋转或平移得到的是( )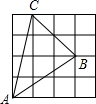 A、
A、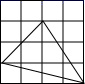 B、
B、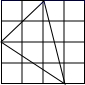 C、
C、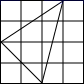 D、
D、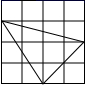 10. 某工程队承接了80万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了35%,结果提前40天完成了这一任务;设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )A、 B、 C、 D、11. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( )
10. 某工程队承接了80万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了35%,结果提前40天完成了这一任务;设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )A、 B、 C、 D、11. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、12. 如图,菱形 的边长为13,对角线 ,点E、F分别是边 、 的中点,连接 并延长与 的延长线相交于点G,则 ( )
A、 B、 C、 D、12. 如图,菱形 的边长为13,对角线 ,点E、F分别是边 、 的中点,连接 并延长与 的延长线相交于点G,则 ( )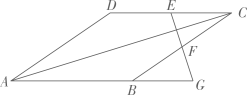 A、13 B、10 C、12 D、5
A、13 B、10 C、12 D、5二、填空题
-
13. 已知 ,则代数式 的值为.14. 关于x的分式方程 有增根,则m的值是 .15. 某手表厂抽查了10只手表的日走时误差,数据如下表所示(单位:s):
日走时误差
0
1
2
3
只数
3
4
2
1
则这10只手表的平均日走时误差是s.
16. 如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节 间的距离.若 间的距离调节到60cm,菱形的边长 ,则 的度数是 . 17. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .
17. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .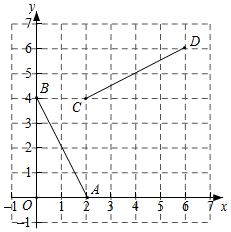
三、解答题
-
18. 分解因式:(1)、3a2-6a+3;(2)、2x3-32x.19. 计算:(1)、 ;(2)、已知 ,且 ,求 的值.20. 某公司员工的月工资如下:
员工
经理
副经理
职员
职员
职员
职员
职员
职员
杂工
月工资/元
7000
4400
2400
2000
1900
1800
1800
1800
1200

经理、职员 、职员 从不同的角度描述了该公司员工的收入情况.设该公司员工的月工资数据(见上述表格)的平均数、中位数、众数分别为 、 、 ,请根据上述信息完成下列问题:
(1)、 , , ;(2)、上月一个员工辞职了,从本月开始,停发该员工工资.若本月该公司剩下的8名员工的月工资不变,但这8名员工的月工资数据(单位:元)的平均数比原9名员工的月工资数据(见上述表格)的平均数减小了.你认为辞职的那名员工可能是 .21. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上. (1)、将 向下平移5个单位得到 ,并写出点 的坐标;(2)、画出 绕点 逆时针旋转90°后得到的 ,并写出点 的坐标;22. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)、将 向下平移5个单位得到 ,并写出点 的坐标;(2)、画出 绕点 逆时针旋转90°后得到的 ,并写出点 的坐标;22. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF. (1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.23. 某地有甲、乙两家口罩厂,已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且乙厂单独完成60万只口罩的生产比甲厂单独完成多用5天.(1)、求甲、乙厂每天分别可以生产多少万只口罩?(2)、该地委托甲、乙两厂尽快完成100万只口罩的生产任务,问两厂同时生产至少需要多少天才能完成生产任务?24. 问题情境:
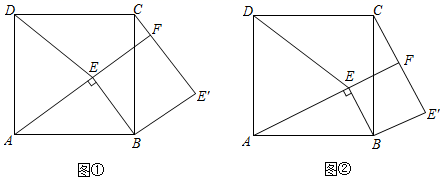
(1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.23. 某地有甲、乙两家口罩厂,已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且乙厂单独完成60万只口罩的生产比甲厂单独完成多用5天.(1)、求甲、乙厂每天分别可以生产多少万只口罩?(2)、该地委托甲、乙两厂尽快完成100万只口罩的生产任务,问两厂同时生产至少需要多少天才能完成生产任务?24. 问题情境:如图1,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE′(点A的对应点为点C).延长AE交CE′于点F,连接DE.
猜想证明:
(1)、试判断四边形BE'FE的形状,并说明理由;(2)、如图2,若DA=DE,请猜想线段CF与FE'的数量关系并加以证明.