山东省烟台招远市（五四制）2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列全国各地地铁标志图中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（）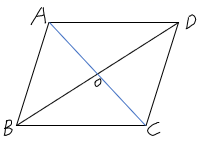

A、∠ABD＝∠BDC，OA＝OC B、∠ABC＝∠ADC，AB＝CD C、∠ABC＝∠ADC，AD∥BC D、∠ABD＝∠BDC，∠BAD＝∠DCB

查看试题解析
3. 下列各分式中，是最简分式的是（）

A、 $\frac{6}{2 x}$ B、 $\frac{a b}{a^{2}}$ C、 $\frac{5 y}{x^{2} + 1}$ D、 $\frac{x^{2} + x}{x y}$

查看试题解析
4. 已知平行四边形ABCD中，∠A＋∠C＝110°，则∠B的度数为（）

A、125° B、135° C、145° D、155°

查看试题解析
5. 如图，点A，B的坐标分别为（1，1）、（3，2），将△ABC绕点A按逆时针方向旋转90°，得到△A'B'C'，则B'点的坐标为（）

A、（﹣1，3） B、（－1，2） C、（0，2） D、（0，3）

查看试题解析
6. 下列多项式中，不能用乘法公式进行因式分解的是（）

A、a²﹣1 B、a²+2a+1 C、a²+4 D、9a²﹣6a+1

查看试题解析
7. 如图，在平行四边形ABCD中，DE平分∠ADC交BC边于点E，已知BE＝4cm，AB＝6cm，则AD的长度是（）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
8. 如图，将△ABC向右平移8个单位长度得到△DEF，且点B，E，C，F在同一条直线上，若EC＝4，则BC的长度是（）

A、11 B、12 C、13 D、14

查看试题解析
9. 小明同学对数据26，36，46，5□，52进行统计分析，发现其中一个两位数的个位数字被黑水涂污看不到了，则计算结果与被涂污数字无关的是（）

A、平均数 B、中位数 C、方差 D、极差

查看试题解析
10. 证明：平行四边形对角线互相平分．
已知：四边形ABCD是平行四边形，如图所示．

求证： $A O = C O$ ， $B O = D O$

以下是排乱的证明过程，正确的顺序应是

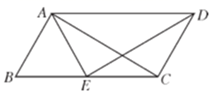
① $∵ ∠ A B O = ∠ C D O$ ， $∠ B A C = ∠ D C A$ ．② $∵$ 四边形ABCD是平行四边形．③ $∴ A B ∥ C D$ ， $A B = D C$ ．④ $Δ A O B ≅ Δ C O D$ ．⑤ $∴ O A = O C$ ， $O B = O D$ （）

A、②①③④⑤ B、②③⑤①④ C、②③①④⑤ D、③②①④⑤

查看试题解析
11. 如图，已知△ABC中，点M是BC边上的中点，AN平分∠BAC，BN⊥AN于点N，若AB＝8，MN＝2，则AC的长为（）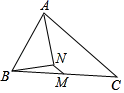

A、12 B、11 C、10 D、9

查看试题解析
12. 如图，在△ABC中，AB＝AC，∠B＝30°，点D、E分别为AB、AC上的点，且DE∥BC．将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上，连接BD、EC．下列结论：①△ADE的旋转角为120°；②BD＝EC；③BE＝AD+AC；④DE⊥AC，其中正确的有（）

A、②③ B、②③④ C、①②③ D、①②③④

查看试题解析

二、填空题

13. 已知一个多边形的内角和是外角和的 $\frac{3}{2}$ ，则这个多边形的边数是

查看试题解析
14. 若一组数据x₁＋1，x₂＋1，…，x_n＋1的平均数为10，方差为1，则另一组数据3x₁＋2，3x₂＋2，…，3x_n＋2的方差是．

查看试题解析
15. 已知关于 $x$ 的方程 $\frac{2 x - m}{x - 1} = 1$ 的解是正数，则 $m$ 的取值范围为.

查看试题解析
16. 如图，点A、B分别在x轴和y轴上，OA＝1，OB＝2，若将线段AB平移至 $A' B'$ ，则a＋b的值为．

查看试题解析
17. 如图，在平行四边形ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB＝8，EF＝1，则BC长为．

查看试题解析
18. 如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是．

查看试题解析

三、解答题

19. 化简求值： $(1+ \frac{1}{a}) \div \frac{a^{2} - 1}{a} - \frac{2 a - 2}{a^{2} - 2 a + 1}$ ，a取﹣1、0、1、2中的一个数．

查看试题解析
20. 如图，在正方形网格中，△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：

(1)、作出△ABC关于原点O成中心对称的△A₁B₁C₁ ，写出B₁的坐标；

(2)、直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．

查看试题解析
21. 某校八年级（1）班甲、乙两男生在5次引体向上测试中有效次数如下：
甲：8，8，7，8，9；乙：5，9，7，10，9；

甲乙两同学引体向上的平均数、众数、中位数、方差如下：

平均数

众数

中位数

方差

甲

8

b

8

0.4

乙

a

9

c

3.2

根据以上信息，回答下列问题：

(1)、表格是a＝， b＝， c＝．（填数值）

(2)、体育老师根据这5次的成绩，决定选择甲同学代表班级参加年级引体向上比赛，选择甲的理由是．班主任李老师根据去年比赛的成绩（至少9次才能获奖），决定选择乙同学代表班级参加年级引体向上比赛，选择乙的理由是；

(3)、如果乙同学再做一次引体向上，有效次数为8，那么乙同学6次引体向上成绩的平均数，中位数，方差．（填“变大”、“变小”或“不变”）

查看试题解析
22. 如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.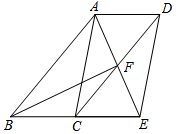

(1)、求证：BE＝CD；

(2)、若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形.

查看试题解析
23. 春节是我国的传统节日，人们素有吃水饺的习俗．某商场在年前准备购进A、B两种品牌的水饺进行销售，据了解，用3000元购买A品牌水饺的数量（袋）比用2880元购买B品牌水饺的数量（袋）多40袋，且B品牌水饺的单价（元/袋）是A品牌水饺单价（元/袋）的1.2倍．

(1)、求A、B两种品牌水饺的单价各是多少？

(2)、若计划购进这两种品牌的水饺共220袋销售，且购买A品牌水饺的费用不多于购买B品牌水饺的费用，写出总费用w（元）与购买A品牌水饺数量m（袋）之间的关系式，并求出如何购买才能使总费用最低？最低是多少？

查看试题解析
24. 如图，在 $▱$ ABCD中，E为BC边上一点，且AB=AE ．

(1)、求证：△ABC≌△EAD；

(2)、若AE平分∠DAB ， ∠EAC=25°，求∠AED的度数．

查看试题解析
25. 在△ABC中，AB＝AC，点D在边BC所在的直线上，过点D作DE∥AC交直线AB于点E，DF∥AB交直线AC于点F．

(1)、当点D在边BC上时，如图①，求证：DE＋DF＝AC；

(2)、当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE、DF、AC之间的等量关系式（不需要证明）；

(3)、若AC＝10，DE＝7，问：DF的长为多少？

查看试题解析

	平均数	众数	中位数	方差
甲	8	b	8	0.4
乙	a	9	c	3.2