山东省烟台市龙口市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式由左边到右边的变形中，属于分解因式的是（）

A、a（x+y）=ax+ay B、x²﹣4x+4=x（x﹣4）+4 C、10x²﹣5x=5x（2x﹣1） D、x²﹣16+6x=（x+4）（x﹣4）+6x

查看试题解析
3. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x的值为（）

A、2 B、-2 C、±2 D、4

查看试题解析
4. 如果一组数据6，﹣2，0，6，2，x的平均数是2，那么这组数据的极差为（）

A、12 B、8 C、6 D、-8

查看试题解析
5. 如图，在平行四边形ABCD中，AE⊥BC于点E，AF⊥CD于点F．若∠EAF=58°，则∠B的度数为（）

A、52° B、58° C、62° D、68°

查看试题解析
6. 如果解关于x的分式方程 $\frac{m}{x - 2} - \frac{2 x}{2 - x} = 1$ 时出现增根，那么m的值为（）

A、-2 B、2 C、4 D、-4

查看试题解析
7. 若正多边形的一个外角是 $45 °$ ，则该正多边形的内角和为（）

A、 $540 °$ B、 $900 °$ C、 $1080 °$ D、 $1440 °$

查看试题解析
8. 如图，△DEF是由△ABC平移得到的，对于以下结论：①BC=EF；②AB $//$ DE；③△ABC≌△DEF；④四边形ACFD为平行四边形，正确的是（）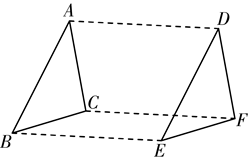

A、①②③ B、②③④ C、①③④ D、①②③④

查看试题解析
9. 已知 $P = m - 4$ ， $Q = m^{2} - 3 m$ ，则P与Q的大小关系为（）

A、P≤Q B、P＜Q C、P=Q D、P＞Q

查看试题解析
10.
在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（　　）

A、① B、② C、③ D、④

查看试题解析
11. 如图，将△ABC绕点P逆时针旋转90°得到△A′B′C′，则点P的坐标是（）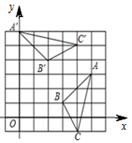

A、（1，2） B、（2，1） C、（1，1） D、（1，3）

查看试题解析
12. 如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF，CF，则下列结论：①∠DCF= $\frac{1}{2}$ ∠BCD；②∠DFC+∠ECF=90^o；③S_△CEF＞S_△CDF；④∠EFC=∠BCF+∠AEF，其中正确结论的个数是（）

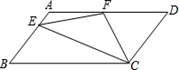A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式： $x^{m + 3} - x^{m + 1}$ =.

查看试题解析
14. 已知a²+3ab+b²=0（a≠0，b≠0），则代数式 $\frac{b}{a}$ + $\frac{a}{b}$ 的值等于．

查看试题解析
15. 已知ab=7，a+b=2，则多项式a²b+ab²+2005的值为．

查看试题解析
16. 某投掷运动员在一次测试中，8次成绩统计如图所示，这组成绩的中位数是．

查看试题解析
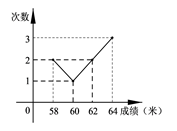17. 如图，在平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上一点E，且BE=8，CE=6，则AB的长是．

查看试题解析
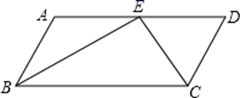18. 如图，四边形ABCD中，BC $//$ AD，AD=8，BC=3．E，F分别是AC，BD的中点，则EF= ．

查看试题解析
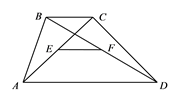19. 若关于x的方程 $\frac{2 m x - 1}{x + 2} = 1$ 的解为负数，则m的取值范围为．

查看试题解析
20. 如图，平行四边形ABCD中，AB=6cm，AD=9cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒3cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），设运动时间为t秒．在运动以后，当t=秒时，以P，D，Q，B四点恰好组成平行四边形．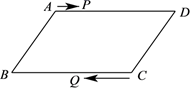

查看试题解析

三、解答题

21. 分解因式：

(1)、 $- x^{3} + 6 x^{2} - 9 x$ ；

(2)、 ${(2 a + b)}^{2} - {(a + 2 b)}^{2}$

查看试题解析
22. 先化简再求值： $(\frac{a^{2} + b^{2}}{2 a} - b) \div \frac{a b - b^{2}}{a b}$ ，已知 $a = b - 4$ ．

查看试题解析
23. 近年来，我国逐步完善养老金保险制度，甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元，甲计划比乙每年多缴纳养老保险金0.2万元．求甲、乙两人计划每年分别缴纳养老保险金多少万元？

查看试题解析
24. 如图是交警在一个路口统计的某个时段来往车辆的车速情况（单位：千米/时）

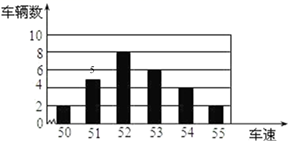(1)、写出该时段来往车辆车速的众数；

(2)、计算这些车的平均速度；（结果精确到0.1千米/时）

查看试题解析
25. 如图，在平行四边形ABCD中，延长AD到点E，延长CB到点F，使得DE=BF，连接EF，分别交CD，AB于点G，H，连接AG，CH．
求证：四边形AGCH是平行四边形．

查看试题解析
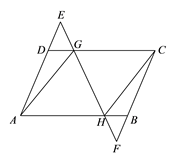26. 某市举行学科知识竞赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．

查看试题解析
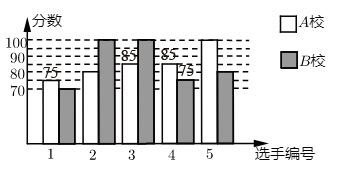27. 仔细阅读下面例题，解答问题：
例题：已知二次三项式 $x^{2} - 4 x + m$ 中有一个因式是 $x + 3$ ，求另一个因式以及m的值．

解：设另一个因式为 $x + n$ ，得 $x^{2} - 4 x + m = (x + 3) (x + n)$ ．

∴ ${\begin{array}{l} 3 + n = - 4 \\ m = 3 n \end{array}$ 解得 $n = - 7 ， m = - 21$

另一个因式为 $x - 7$ ，m的值为-21．

仿照以上方法解答下面问题：

已知二次三项式 $2 x^{2} + 3 x - k$ 有一个因式是 $x - 5$ ，求另一个因式以及k的值．

查看试题解析
28. 如图1，在Rt△ABC中，∠C＝90°，AC＝BC，点D，E分别在边AC，BC上，CD＝CE，连接AE，点F，H，G分别为DE，AE，AB的中点连接FH，HG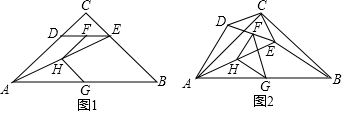

(1)、观察猜想图1中，线段FH与GH的数量关系是，位置关系是

(2)、探究证明：把△CDE绕点C顺时针方向旋转到图2的位置，连接AD，AE，BE判断△FHG的形状，并说明理由

(3)、拓展延伸：把△CDE绕点C在平面内自由旋转，若CD＝4，AC＝8，请直接写出△FHG面积的最大值

查看试题解析