山东省烟台市莱阳市2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列手机手势解锁图案中,属于中心对称图形的是( )A、
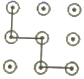 B、
B、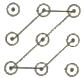 C、
C、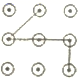 D、
D、 2. 下列各式从左到右的变形,是因式分解且分解结果正确的为( )A、 B、 C、 D、3. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
2. 下列各式从左到右的变形,是因式分解且分解结果正确的为( )A、 B、 C、 D、3. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( ) A、①,② B、①,④ C、③,④ D、②,③4. 下列计算错误的是( )A、 B、 C、 D、5. 一组数据由5个整数组成,已知中位数是10,唯一众数是12,则这组数据和的最大值可能是( )A、50 B、51 C、52 D、536. 在平面直角坐标系中,把点(-4,2)先向左平移1个单位长度,再向上平移2个单位长度,得到的点的坐标是( )A、(-5,4) B、(-5,0) C、(-3,4) D、(-3,0)7. 下列各式:①﹣x2﹣y2;②﹣ a2b2+1; ③a2+ab+b2; ④﹣x2+2xy﹣y2;⑤ ﹣mn+m2n2 , 用公式法分解因式的有( )A、2个 B、3个 C、4个 D、5个8. 若 、 的值均扩大为原来的2倍,则下列分式的值保持不变的是( )A、 B、 C、 D、9. 一次演讲比赛中五名同学的成绩如下表所示,其中有两个数据被遮盖,那么被遮盖的两个数据依次是( )
A、①,② B、①,④ C、③,④ D、②,③4. 下列计算错误的是( )A、 B、 C、 D、5. 一组数据由5个整数组成,已知中位数是10,唯一众数是12,则这组数据和的最大值可能是( )A、50 B、51 C、52 D、536. 在平面直角坐标系中,把点(-4,2)先向左平移1个单位长度,再向上平移2个单位长度,得到的点的坐标是( )A、(-5,4) B、(-5,0) C、(-3,4) D、(-3,0)7. 下列各式:①﹣x2﹣y2;②﹣ a2b2+1; ③a2+ab+b2; ④﹣x2+2xy﹣y2;⑤ ﹣mn+m2n2 , 用公式法分解因式的有( )A、2个 B、3个 C、4个 D、5个8. 若 、 的值均扩大为原来的2倍,则下列分式的值保持不变的是( )A、 B、 C、 D、9. 一次演讲比赛中五名同学的成绩如下表所示,其中有两个数据被遮盖,那么被遮盖的两个数据依次是( )组员及项目
甲
乙
丙
丁
戊
方差
平均成绩
得分
81
79
■
80
82
■
80
A、80,2 B、80, C、78,2 D、78,10. 如图, 是 的边 延长线上一点,连接 , , , 交 于点 ,添加以下条件,不能判定四边形 为平行四边形的是( )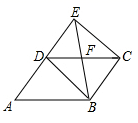 A、 B、 C、 D、11. 如图,在五边形 中, , , 分别平分 , ,则 的度数( )
A、 B、 C、 D、11. 如图,在五边形 中, , , 分别平分 , ,则 的度数( )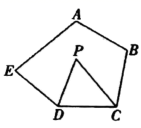 A、70° B、65° C、60° D、55°12. 如图, 绕点 逆时针旋转50°后能与 重合,若 ,则 的度数为( )
A、70° B、65° C、60° D、55°12. 如图, 绕点 逆时针旋转50°后能与 重合,若 ,则 的度数为( )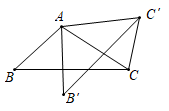 A、45° B、40° C、35° D、30°
A、45° B、40° C、35° D、30°二、填空题
-
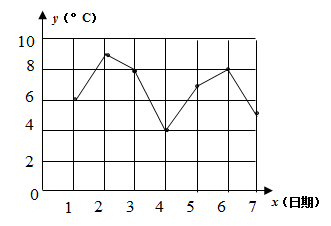
13. 多项式 , 与 的公因式为 .14. 若关于 的分式方程 有增根,则 的值是 .15. 已知点 和点 关于原点对称,则x+y等于 .16. 一个正多边形的每一个内角比每一个外角的5倍还小60°,则这个正多边形的内角和是 .17. 如图是某市一周内日平均气温变化统计图,若日平均气温数据都是整数,则这组数据的中位数是℃.
 18. 如图,在 中, 平分 , 于点 ,交BC于点F,点 是 的中点,若 , ,则 的长为 .
18. 如图,在 中, 平分 , 于点 ,交BC于点F,点 是 的中点,若 , ,则 的长为 .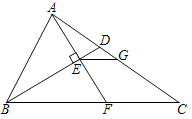
三、解答题
-
19. 把下列各式因式分解:(1)、(2)、20.(1)、先化简,再求值: ,其中 .(2)、解方程: .21. 在直角坐标系中,将 平移后得到 ,它们的三个顶点坐标如表所示:
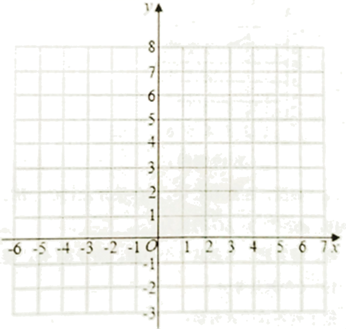 (1)、观察表中各对应点坐标的变化填空: , ;(2)、 向平移个单位长度,再向平移个单位长度可以得到 ;(3)、在坐标系中画出 及平移后的 .22. 如图,平行四边形ABCD的对角线AC , BD交于点O , M , N分别是AB , AD的中点.
(1)、观察表中各对应点坐标的变化填空: , ;(2)、 向平移个单位长度,再向平移个单位长度可以得到 ;(3)、在坐标系中画出 及平移后的 .22. 如图,平行四边形ABCD的对角线AC , BD交于点O , M , N分别是AB , AD的中点.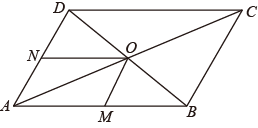 (1)、求证:四边形AMON是平行四边形;(2)、若AC=6,BD=4,∠AOB=90°,求NO的长度.23. 李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有48分钟,于是他立即步行(匀速)回家,在家拿道具用了2分钟,然后立即骑自行车(匀速)返回学校。已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.(1)、李明步行的速度是多少?(2)、李明能否在联欢会开始前赶到学校?24. 小明与小东是某中学篮球队的队员,在最近五场球赛中的得分如表所示:
(1)、求证:四边形AMON是平行四边形;(2)、若AC=6,BD=4,∠AOB=90°,求NO的长度.23. 李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有48分钟,于是他立即步行(匀速)回家,在家拿道具用了2分钟,然后立即骑自行车(匀速)返回学校。已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.(1)、李明步行的速度是多少?(2)、李明能否在联欢会开始前赶到学校?24. 小明与小东是某中学篮球队的队员,在最近五场球赛中的得分如表所示:第一场
第二场
第三场
第四场
第五场
小明
10
13
9
8
10
小东
12
2
13
21
2
(1)、根据上表所给的数据,填写下表:平均数
中位数
众数
方差
小明
10
10
2.8
小东
10
12
32.4
(2)、根据以上信息,若教练选择小明参加下一场比赛,教练的理由是什么?(3)、若小明的下一场球赛得分是16分,则小明六场球赛得分的平均数、中位数、众数、方差分别是多少?25. 如图,四边形ABCD中,BE⊥AC交AD于点G,DF⊥AC于点F,已知AF=CE,AB=CD. (1)、求证:四边形ABCD是平行四边形;(2)、如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.
(1)、求证:四边形ABCD是平行四边形;(2)、如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.