山东省烟台市福山区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±12. 下列关于数字变换的图案中,既是中心对称图形也是轴对称图形的有( )
 A、4个 B、3个 C、2个 D、1个3. 下列各式从左到右的变形属于分解因式的是( )A、 B、 C、 D、4. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A、4个 B、3个 C、2个 D、1个3. 下列各式从左到右的变形属于分解因式的是( )A、 B、 C、 D、4. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( ) A、30° B、90° C、120° D、180°5. 下列命题中,正确的命题是( )A、菱形的对角线互相平分且相等 B、顺次联结菱形各边的中点所得的四边形是矩形 C、矩形的对角线互相垂直平分 D、顺次连结矩形各边的中点所得的四边形是正方形6. 如图,菱形 中,E,F分别是 , 的中点,若 ,则菱形 的周长为( )
A、30° B、90° C、120° D、180°5. 下列命题中,正确的命题是( )A、菱形的对角线互相平分且相等 B、顺次联结菱形各边的中点所得的四边形是矩形 C、矩形的对角线互相垂直平分 D、顺次连结矩形各边的中点所得的四边形是正方形6. 如图,菱形 中,E,F分别是 , 的中点,若 ,则菱形 的周长为( )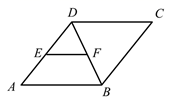 A、20 B、30 C、40 D、507. 下表是某地援鄂医疗人员的年龄分布
A、20 B、30 C、40 D、507. 下表是某地援鄂医疗人员的年龄分布年龄/岁
29
30
31
32
频数
15
20
对于不同的 下列关于年龄的统计量不会发生改变的是( )
A、众数、中位数 B、众数、方差 C、平均数、方差 D、平均数、中位数8. 利用计算器求一组数据的平均数.其按键顺序如下: ,则输出的结果为( ) A、1 B、3.5 C、4 D、99. 用尺现作图的方法在一个平行四边形内作菱形 ,下列作法错误的是 ( )A、
,则输出的结果为( ) A、1 B、3.5 C、4 D、99. 用尺现作图的方法在一个平行四边形内作菱形 ,下列作法错误的是 ( )A、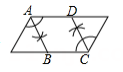 B、
B、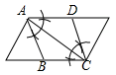 C、
C、 D、
D、 10. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、11. 如图,点 是矩形 的对角线上一点,过点 作 ,分别交 于 ,连接 ,若 ,则图中阴影部分的面积为( )
10. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、11. 如图,点 是矩形 的对角线上一点,过点 作 ,分别交 于 ,连接 ,若 ,则图中阴影部分的面积为( ) A、3 B、6 C、9 D、1212. 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )
A、3 B、6 C、9 D、1212. 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )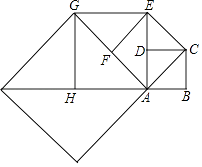 A、( )n﹣1 B、2n﹣1 C、( )n D、2n
A、( )n﹣1 B、2n﹣1 C、( )n D、2n二、填空题
-
13. 已知正多边形的一个外角等于 则这个正多边形的内角和的度数为 .14. 关于x的方程 的解为正数,则k的取值范围是.15. 在线上教学期间,某校落实市教育局要求,督促学生每天做眼保健操.为了解落实情况,学校随机抽取了部分学生进行调查,调查结果分为四类(A类:总时长 分钟;B类:5分钟 总时长 分钟;C类:10分钟 总时长 分钟;D类:总时长 15分钟),将调查所得数据整理并绘制成如下两幅不完整的统计图.
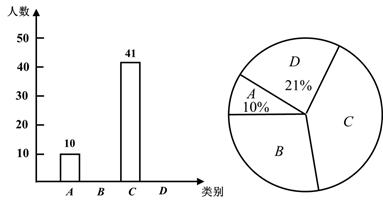
该校共有1200名学生,请根据以上统计分析,估计该校每天做眼保健操总时长超过5分钟且不超过10分钟的学生约有人.
16. 如图,在 中,点 分别在边 上,且 ,连接 ,点 分别是 的中点, ,则 的度数是 .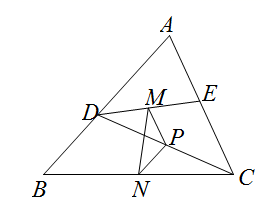 17. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .
17. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .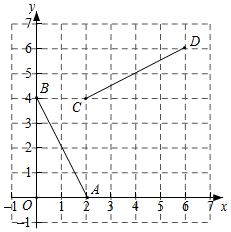 18. 如图,在菱形 中, ,将菱形 绕点 逆时针方向旋转,对应得到菱形 点 在 上. 与 交于点 则 的长是 .
18. 如图,在菱形 中, ,将菱形 绕点 逆时针方向旋转,对应得到菱形 点 在 上. 与 交于点 则 的长是 .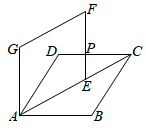
三、解答题
-
19.(1)、先化简,再求值: ,已知 .(2)、先化简,再求值: ,从 中选出合适的 的整数值代入求值.20. 如图所示,网格中每个小正方冠的边长为 ,请你认真观察图(1)中的三个网格中阴影部分构成的图案.解答下列问题:
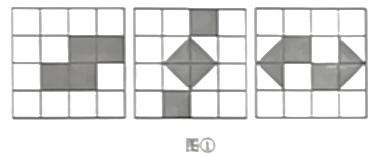
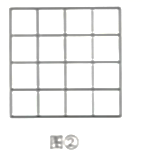 (1)、图①中的三个图案面积都是 , 且都具有一个共同特征:都是对称图形;(2)、请在图②中设计出一个面积与图①阴影部分面积相同,且具备上述共同特征的图案,要求所画图案不能与图①中所给出的图案相同.21. 如图,在小正方形组成的网格中, 和 的顶点都在格点上,根据图形解答下列问题;
(1)、图①中的三个图案面积都是 , 且都具有一个共同特征:都是对称图形;(2)、请在图②中设计出一个面积与图①阴影部分面积相同,且具备上述共同特征的图案,要求所画图案不能与图①中所给出的图案相同.21. 如图,在小正方形组成的网格中, 和 的顶点都在格点上,根据图形解答下列问题;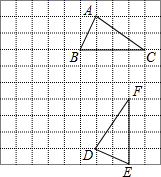
⑴将 向左平移4个单位长度,再向下平移2个单位长度,画出平移后的
⑵将 绕点 逆时针旋转 ,画出旋转后的
22. 如图是某商场第二季度某品牌运动服装的 号, 号, 号, 号, 号销售情况的扇形统计图和条形统计图.
根据图中信息解答下列问题:
(1)、求 号, 号运动服销量的百分比;(2)、补全条形统计图:该商场第三季度继续销售该品牌运动服 件,根据以上统计结果, 号运动服应该进多少件较为合适?(3)、按照 号, 号运动服装的销量比,从 号、 号运动服装中分别取出 件、 件,若再取 件 号运动服装,将它们放在一起,现从这 件运动服装中,随机取出 件,取得 号运动服装的概率为 ,求 的值23. 如图,在平行四边形 中,对角线 与 交于点O,点M,N分别为 、 的中点,延长 至点E,使 ,连接 .
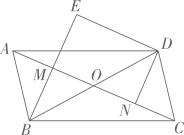 (1)、求证: ;(2)、若 ,且 , ,求四边形 的面积.24. 某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.(1)、求第一次每个足球的进价是多少元?(2)、若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?25. 如图,矩形 的顶点 分别在菱形 的边 上,顶点 在菱形 的对角线 上.
(1)、求证: ;(2)、若 ,且 , ,求四边形 的面积.24. 某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.(1)、求第一次每个足球的进价是多少元?(2)、若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?25. 如图,矩形 的顶点 分别在菱形 的边 上,顶点 在菱形 的对角线 上.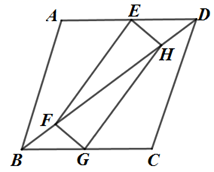 (1)、求证: ;(2)、若 为 中点, ,求菱形 的周长;26. 如图
(1)、求证: ;(2)、若 为 中点, ,求菱形 的周长;26. 如图 (1)、操作发现
(1)、操作发现如图1,在五边形 中, , , ,试猜想 , , 之间的数量关.小明地过仔细思考,得到如下解题思路:
将 绕点 逆时针旋转 至 .由 ,得 ,即点 , , 三点共线,易证 , 被 , , 之间的数量关系是;
(2)、类比探究如图2,在四边形 中, , ,点 , 分别在边 , 的延长线上, ,连接 ,试猜想 , , 之间的数量关系,并给出证明.
(3)、拓展延伸如图3,在 中, , ,点 , 均在边 上,且 ,若 , ,则 的长为.