山东省烟台蓬莱市（五四制）2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列智能手机的功能图标中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x^{2} - 1}{x + 1}$ 值为0，则x的值为（）

A、1 B、±1 C、-2 D、2

查看试题解析
3. 下列因式分解正确的是（）

A、 $a (a - b) - b (a - b) = (a - b) (a + b)$ B、 $a^{2} - 9 b^{2} = {(a - 3 b)}^{2}$ C、 $a^{2} + 4 a b + 4 b^{2} = {(a + 2 b)}^{2}$ D、 $a^{2} - a b + a = a (a - b)$

查看试题解析
4. 篮球小组共有15名同学，在一次投篮比赛中，他们的成绩如右面的条形图所示，这15名同学进球数的众数和中位数分别是（）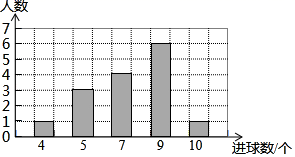

A、6，7 B、7，9 C、9，7 D、9，9

查看试题解析
5. 如图，在平面直角坐标系 $x O y$ 中， $Δ AOB$ 可以看作是由 $Δ OCD$ 经过两次图形的变化（平移、轴对称、旋转）得到的，这个变化过程不可能是（）

A、先平移，再轴对称 B、先轴对称，再旋转 C、先旋转，再平移 D、先轴对称，再平移

查看试题解析
6. 若正多边形的一个外角是45°，则该正多边形从一个顶点出发的对角线的条数为（）

A、4 B、5 C、6 D、8

查看试题解析
7. 如图在▱ABCD中，已知AC=4cm，若△ACD的周长为13cm，则▱ABCD的周长为（）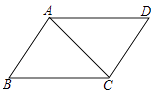

A、26cm B、24cm C、20cm D、18cm

查看试题解析
8. 已知四边形 $A B C D$ ，对角线 $A C$ 和 $B D$ 交于点O，从下列条件中：① $A B / / C D$ ；② $A D = B C$ ；③ $∠ A B C = ∠ A D C$ ；④ $O A = O C$ ．任选其中两个，以下组合能够判定四边形 $A B C D$ 是平行四边形的是（）

A、①④ B、②③ C、②④ D、③④

查看试题解析
9. 如图，网格纸上正方形小格的边长为1．图中线段AB和点P绕着同一个点做相同的旋转，分别得到线段A'B'和点P'，则点P'所在的单位正方形区域是（）

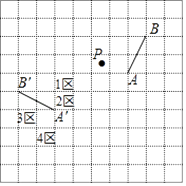A、1区 B、2区 C、3区 D、4区

查看试题解析
10. 若 $\frac{1}{a} - \frac{1}{b} = \frac{1}{3}$ ，则 $\frac{a b}{a - b}$ 的值是（）

A、-3 B、 $- \frac{1}{3}$ C、3 D、 $- \frac{1}{3}$

查看试题解析
11. 已知 $M = m - 4$ ， $N = m^{2} - 3 m$ ，则M与N的大小关系为（）

A、 $M > N$ B、 $M \leq N$ C、 $M = N$ D、 $M < N$

查看试题解析
12. 如图，四边形ABCD中，点E、F、G、H分别是线段AB、CD、AC、BD的中点，则四边形EGFH的周长（）

A、只与AB、CD的长有关 B、只与AD、BC的长有关 C、只与AC、BD的长有关 D、与四边形ABCD各边的长都有关

查看试题解析

二、填空题

13. 如果 $m^{2} - m - 3 = 0$ ，那么代数式 $(m - \frac{1}{m}) \div \frac{m + 1}{m^{2}}$ 的值是．

查看试题解析
14. 若将 $3 x^{2} - m x + n$ 进行因式分解的结果为 $(3 x + 2) (x - 1)$ ，则mn= ．

查看试题解析
15. 某市对旧城区规划改建，根据2001年至2003年发展情况调查，制作成了房地产开发公司个数的条形图和各年度每个房地产开发公司平均建筑面积情况的条形图，利用统计图提供的信息计算出这3年中该市平均每年的建筑面积是万平方米．

查看试题解析
16. 如图，在菱形 $A B C D$ 中， $∠ B = 50 °$ ，点 $E$ 在 $C D$ 上，若 $A E = A C$ ，则 $∠ B A E =$ ．

查看试题解析
17. 如图，矩形ABCD中，直线MN垂直平分AC，与CD，AB分别交于点M，N．若DM＝2，CM＝3，则矩形的对角线AC的长为．

查看试题解析
18. 如图，将正方形OEFG放在平面直角坐标系中，O是坐标原点，点E的坐标为（2，3），则点F的坐标为．

查看试题解析

三、解答题

19. 将下列各式因式分解：

(1)、 $4 x^{2} (x - y) + (y - x)$

(2)、 $x^{2} + 2 x - 15$

查看试题解析
20. 先化简，再求值： $\frac{a^{2} - 9}{a^{2} - 3 a} \div (\frac{a^{2} + 9}{a} + 6)$ ，其中a是整数，且满足 $- 3 \leq a \leq 3$ ，请取一个合适的a值代入求值．

查看试题解析
21. 直角坐标系中，A，B，P的位置如图所示，按要求完成下列各题：

⑴将线段AB向左平移5个单位，再向下平移1个单位，画出平移后的线段A₁B₁；

⑵将线段AB绕点P顺时针旋转90°，画出旋转后的线段A₂B₂；

⑶作出线段AB关于点P成中心对称的线段A₃B₃ ．

查看试题解析

22. 6月26日是“国际禁毒日”某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动，为了解竞赛情况，从两个年级各抽取10名学生的成绩（满分为100分），收集数据为：七年级90，95，95，80，85，90，85，90，85，100；八年级：85，85，95，80，95，90，90，90，100，90；

整理数据：

	80	85	90	95	100
七年级	2	2	3	2	1
八年级	1	2	4	$a$	1

分析数据：

	平均数	中位数	众数	方差
七年级	89	$b$	90	39
八年级	$c$	90	$d$	30

根据以上信息回答下列问题：

(1)、请直接写出表格中

a ， b ， c ， d

的值

(2)、通过数据分析，你认为哪个年级的成绩比较好？说明理由；

(3)、该校七八年级共600人，本次竞赛成绩不低于90分的为“优秀”估计这两个年级共多少名学生达到“优秀”？

查看试题解析

23. 如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F.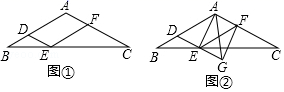

(1)、求证：四边形ADEF为平行四边形；

(2)、当点D为AB中点时，判断▱ADEF的形状；

(3)、延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由.

查看试题解析
24. 某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．

(1)、求该公司购买的A、B型芯片的单价各是多少元？

(2)、若两种芯片共购买了200条，且购买A型芯片的数量不超过B型芯片数量的 $\frac{1}{3}$ ，不小于B型芯片数量的 $\frac{1}{4}$ ，求如何购买，才能使购买总费用最低？最低是多少元？

查看试题解析
25. 如图1，在Rt△ABC中，∠C＝90°，AC＝BC，点D，E分别在边AC，BC上，CD＝CE，连接AE，点F，H，G分别为DE，AE，AB的中点连接FH，HG

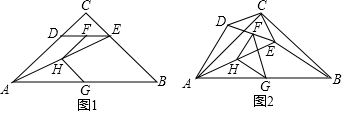(1)、观察猜想图1中，线段FH与GH的数量关系是，位置关系是

(2)、探究证明：把△CDE绕点C顺时针方向旋转到图2的位置，连接AD，AE，BE判断△FHG的形状，并说明理由

(3)、拓展延伸：把△CDE绕点C在平面内自由旋转，若CD＝4，AC＝8，请直接写出△FHG面积的最大值

查看试题解析