山东省潍坊市安丘市2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在一次数学测试中,小明成绩72分,超过班级半数同学的成绩,分折得出这个结论所用的统计量是( )A、中位数 B、众数 C、平均数 D、方差3. 一把直尺与30°的直角三角板如图所示, ,则 ( )
2. 在一次数学测试中,小明成绩72分,超过班级半数同学的成绩,分折得出这个结论所用的统计量是( )A、中位数 B、众数 C、平均数 D、方差3. 一把直尺与30°的直角三角板如图所示, ,则 ( ) A、50° B、60° C、70° D、80°4. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为 ;同时去掉一个最高分和一个最低分,平均分为z,则A、 B、 C、 D、5. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A、50° B、60° C、70° D、80°4. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为 ;同时去掉一个最高分和一个最低分,平均分为z,则A、 B、 C、 D、5. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )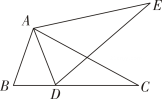 A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED6. 化简 的结果是( )A、a+b B、a﹣b C、 D、7. 一艘轮船在静水中的最大航速为35km/h,它以最大航速沿江顺流航行120km所用时间,与以最大航速逆流航行90km所用时间相等.设江水的流速为vkm/h,则可列方程为( )A、 = B、 = C、 = D、 =8. 如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上, , , ,小敏行走的路线为 ,小聪行走的路线为 .若小敏行走的路程为3100m,则小聪行走的路程为( )
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED6. 化简 的结果是( )A、a+b B、a﹣b C、 D、7. 一艘轮船在静水中的最大航速为35km/h,它以最大航速沿江顺流航行120km所用时间,与以最大航速逆流航行90km所用时间相等.设江水的流速为vkm/h,则可列方程为( )A、 = B、 = C、 = D、 =8. 如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上, , , ,小敏行走的路线为 ,小聪行走的路线为 .若小敏行走的路程为3100m,则小聪行走的路程为( ) A、3100m B、4600m C、5500m D、6100m9. 下列命题中,其逆命题是真命题的有( )个
A、3100m B、4600m C、5500m D、6100m9. 下列命题中,其逆命题是真命题的有( )个①全等三角形的对应角相等,② 两直线平行,同位角相等,③等腰三角形的两个底角相等,④正方形的四个角相等.
A、1 B、2 C、3 D、410. 下列不能判断四边形ABCD是平行四边形的是( )A、AB=CD,AD=BC B、AB∥CD,AD=BC C、AB∥CD,AD∥BC D、∠A=∠C,∠B=∠D11. 如图,已知线段AB,分别以A,B为圆心,大于 AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是( )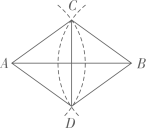 A、AB平分∠CAD B、CD平分∠ACB C、AB⊥CD D、AB=CD12. 如图, 中, , ,要判定四边形DBFE是菱形,可添加的条件是( )
A、AB平分∠CAD B、CD平分∠ACB C、AB⊥CD D、AB=CD12. 如图, 中, , ,要判定四边形DBFE是菱形,可添加的条件是( )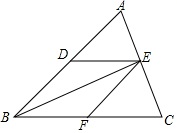 A、 B、 C、 D、BE平分
A、 B、 C、 D、BE平分二、填空题
-
13. 当 时,分式 与 相等.14. 已知 .则分式 的值是 .15. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:cm)的平均数和方差.要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是 .
甲
乙
丙
丁
平均数
376
350
376
350
方差
12.5
13.5
2.4
5.4
16. 如图,将两张对边平行且相等的纸条交叉叠放在一起,则重合部分构成的四边形ABCD菱形(是,或不是).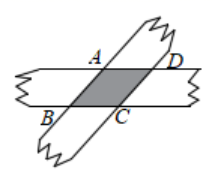 17. 若分式方程 会产生增根,则m的值为.18. 如图, , , ,则 度.
17. 若分式方程 会产生增根,则m的值为.18. 如图, , , ,则 度. 19. 如图,在 中, ,点D、E、F分别是AB、BC、CA的中点.若 ,则线段EF的长是 .
19. 如图,在 中, ,点D、E、F分别是AB、BC、CA的中点.若 ,则线段EF的长是 . 20. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为(用含a,b的代数式表示).
20. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为(用含a,b的代数式表示).
三、解答题
-
21. 观察以下等式:
第1个等式:
第2个等式:
第3个等式:
第4个等式:
第5个等式:
······
按照以上规律.解决下列问题:
(1)、写出第6个等式;(2)、写出你猜想的第n个等式: ▲ (用含 的等式表示),并证明.22. 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N, , . (1)、求证: .(2)、已知 ,连接BN,若N平分 ,求CN的长.23. 为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
(1)、求证: .(2)、已知 ,连接BN,若N平分 ,求CN的长.23. 为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:甲
63
66
63
61
64
61
乙
63
65
60
63
64
63
请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐.
24. 星期天,小明和小芳从同一小区门口同时出发,沿同一路线去离该小区1800米的少年宫参加活动,为响应“节能环保,绿色出行”的号召,两人都步行,已知小明的速度是小芳的速度的1.2倍,结果小明比小芳早6分钟到达,求小芳的速度.