福建省三明市2020-2021学年高一上学期数学期末考试试卷
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 设全集 ,集合 , ,则 ( )A、 B、 C、 D、2. 下列各式中正确的是( )A、 B、 C、 D、3. 下列各组函数中表示同一函数的是( )A、 , B、 , C、 , D、 ,4. 若幂函数 的图象过点 ,则 的值为( )A、5 B、6 C、8 D、95. 函数 的图象大致为( )A、
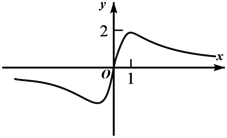 B、
B、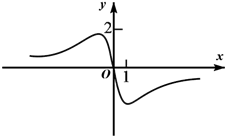 C、
C、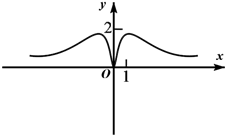 D、
D、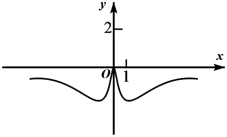 6. 已知a=log20.2,b= ,c= ,则( )A、a<b<c B、a<c<b C、c<a<b D、b<c<a7. 已知角 的顶点与直角坐标系的原点重合,始边与 轴的非负半轴重合,终边落在直 上,则 的值是( )A、 B、 C、 或 D、 或8. 设函数 的定义域为 ,满足 ,且当 时, .若对任意 ,都有 ,则 的取值范围是( )A、 B、 C、 D、
6. 已知a=log20.2,b= ,c= ,则( )A、a<b<c B、a<c<b C、c<a<b D、b<c<a7. 已知角 的顶点与直角坐标系的原点重合,始边与 轴的非负半轴重合,终边落在直 上,则 的值是( )A、 B、 C、 或 D、 或8. 设函数 的定义域为 ,满足 ,且当 时, .若对任意 ,都有 ,则 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 若 ,则下列不等式成立的是( )A、 B、 C、 D、10. 已知函数 ,下列关于 的说法正确的是( )A、 的定义域是 B、 的值域是 C、 的图象过原点 D、当 时, 在定义域上是增函数11. 下列四个命题中为假命题的是( )A、 , B、命题“ , ”的否定是“ , ” C、设 , ,则 是 的必要不充分条件 D、设 , ,则“ ”是“ ”的必要不充分条件12. 随着市民健康意识的提升,越来越多的人走出家门健身,身边的健身步道成了市民首选的运动场所.如图,某公园内有一个以 为圆心,半径为 ,圆心角为 的扇形人工湖 , 、 是分别由 、 延伸而成的两条健身步道.为进一步完善全民健身公共服务体系,主管部门准备在公园内增建三条健身步道,其中一条与 相切于点 ,且与 、 分别相交于 、 ,另两条是分别和湖岸 、 垂直的 、 (垂足均不与 重合).在 区域以内,扇形人工湖 以外的空地铺上草坪,则( )
 A、 的范围是 B、新增步道 的长度可以为 C、新增步道 、 长度之和可以为 D、当点 为 的中点时,草坪的面积为
A、 的范围是 B、新增步道 的长度可以为 C、新增步道 、 长度之和可以为 D、当点 为 的中点时,草坪的面积为三、填空题
-
13. 函数f(x)= 的定义域是 .14. 设函数 , 则满足 的 的值是 .15. 若正实数 , 满足 ,则 的最小值为 .16. 已知 ,则 , .
四、解答题
-
17. 设集合 , .(1)、求 ;(2)、若 ,求实数 的取值范围.18. 已知 ,且 为第四象限角(1)、求 的值;(2)、求 的值.19. 已知函数 .(1)、判断 在 上单调递增还是单调递减,并证明你的判断;(2)、若 , 的最大值与最小值的差为 ,求 的值.20. 某市居民用电收费方式有以下两种,用户可自由选择其中一种
方式一:阶梯式递增电价,即把居民用户每月用电量划分为三档,电价实行分档递增,具体电价如下表:
档数
月均用电量(度)
电价(元/度)
第一档
不超过230度的部分
0.5
第二档
超过230度至420度的部分
0.6
第三档
420度以上的部分
0.8
方式二:阶梯式递增电价基础上实行峰谷分时电价,即先按阶梯式递增电价标准计算各档电量的电费,然后高峰时段 用每度加价0.03元,低谷时段(22:00至次日 )每度降价0.20元,得出用户的总电费.
(1)、假设某居民用户月均电量为 度,按方式一缴费,月均电价为 元,求 关于 的函数解析式;(2)、若该用户某月用电 度 ,其中高峰电量占该月总电量的 ,按方式二缴费,电费为143元,求该月用电量.
