山东省泰安市宁阳县2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 在△ABC中,若∠A+∠B-∠C=0,则△ABC是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形2. 已知现有的8瓶可乐中有2瓶已过了保质期,从这8瓶可乐中随机抽取1瓶,恰好取到已过了保质期的可乐的概率是( )A、 B、 C、 D、3. 若分式 的值为0,则x的值为( )A、2 B、0 C、﹣2 D、 24. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、5. 若式子 中的 、 都扩大2倍,则分式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、缩小2倍6. 在某市举办的主题为“英雄武汉”的网络演讲比赛中,七位选手的得分分别为:88,84,87,90,86,92,94,则这组数据的中位数是( )A、86 B、88 C、90 D、927. 如图,AD,AE分别为△ABC的高线和角平分线,DF⊥AE于点F,当∠ADF=69°,∠C=65°时,∠B的度数为( )
 A、21° B、23° C、25° D、30°8. 10位歌手一年参加公益活动的次数分别为:2,1,3,3,4,5,3,6,5,3这组数据的平均数和众数分别是( )A、3.5,3 B、3,3.5 C、3,3 D、3.5,49. 甲、乙、丙、丁四支仪仗队队员身高的平均数及方差如表所示:
A、21° B、23° C、25° D、30°8. 10位歌手一年参加公益活动的次数分别为:2,1,3,3,4,5,3,6,5,3这组数据的平均数和众数分别是( )A、3.5,3 B、3,3.5 C、3,3 D、3.5,49. 甲、乙、丙、丁四支仪仗队队员身高的平均数及方差如表所示:甲
乙
丙
丁
平均数( )
177
178
178
179
方差
0.7
1.6
1.1
0.9
则身高较为整齐的仪仗队是( )
A、甲 B、乙 C、丙 D、丁10. 一组数据1,2,1,4,2的方差为( )A、1 B、1.2 C、1.5 D、1.611. 若关于x的方程 有增根,则k的值为( ).
A、3 B、1 C、0 D、-112. 计算 所得的结果是( )A、-2 B、2 C、 D、二、填空题
-
13. 小球在如图所示的地板上自由地滚动并随机地停留在某块方砖上,则它最终停留在黑砖上的概率是 .
 14. 已知a>b,则﹣4a+5﹣4b+5.(填>、=或<)15. 如图,直线 与 相交于点 ,若 ,那么 的取值范围是 .
14. 已知a>b,则﹣4a+5﹣4b+5.(填>、=或<)15. 如图,直线 与 相交于点 ,若 ,那么 的取值范围是 .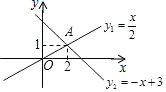 16. 不等式组 的解集是x<m+2,则m的取值范围应为 .17. 如图,在△ABC 中,∠ACB =90°,CD 是 高,∠A =30°,AB =4.则BD = .
16. 不等式组 的解集是x<m+2,则m的取值范围应为 .17. 如图,在△ABC 中,∠ACB =90°,CD 是 高,∠A =30°,AB =4.则BD = .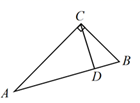 18. 如图,在 中,已知 , , .则 的面积为 .
18. 如图,在 中,已知 , , .则 的面积为 .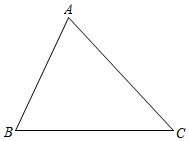
三、解答题
-
19. 分解因式(1)、(2)、(3)、(4)、20.(1)、解不等式 ,并把解集表示在数轴上.(2)、解不等式组 ,并写出它的整数解.(3)、解不等式组: .21. 根据要求解答:(1)、计算: ;(2)、先化简,再求值: ,其中 .(3)、解分式方程 .22. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(不写作法,保留作图痕迹).
 23. 证明命题:如果两个锐角三角形有两边和其中一边上的高分别对应相等,那么这两个三角形全等.(1)、画出图形,写出已知,求证.(2)、写出证明过程.
23. 证明命题:如果两个锐角三角形有两边和其中一边上的高分别对应相等,那么这两个三角形全等.(1)、画出图形,写出已知,求证.(2)、写出证明过程.

