山东省日照市五莲县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 $a^{10} \div a^{2} = a^{5}$ C、 ${(- 3 a^{3})}^{2} = 9 a^{6}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
2. 在下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若等腰三角形的两边长分别为3和7，则这个三角形的周长为（）

A、13 B、17 C、13或17 D、15或17

查看试题解析
4. $m^{a} = 2$ ， $m^{b} = 3$ ， $m^{c} = 4$ ，则 $m^{a + b - c}$ 的值为．（）

A、1 B、1.5 C、2 D、2.5

查看试题解析
5. 一个多边形的内角和是外角和的3倍，则这个多边形是（　　）

A、六边形 B、七边形 C、八边形 D、九边形

查看试题解析
6. 如果多项式 $x^{2} + m x + 16$ 是一个完全平方式，则m的值是（）

A、±4 B、4 C、8 D、± 8

查看试题解析
7. 下列约分结果正确的是（）

A、 $\frac{2}{a + 2} = \frac{1}{a + 1}$ B、 $\frac{a^{2} - b^{2}}{a - b} = a - b$ C、 $\frac{m^{2} - 2 m + 1}{1 - m} = 1 - m$ D、 $\frac{a + b}{a - b} = - 1$

查看试题解析
8. 已知关于 $x$ 的分式方程 $\frac{x - a}{x - 2} = \frac{1}{2}$ 的解是非负数，那么 $a$ 的取值范围是（）

A、 $a \geq 1$ B、 $a \leq 1$ C、 $a \geq 1$ 且 $a \neq 2$ D、 $a \geq 1$ 且 $a \neq 1$

查看试题解析
9. 如图，在 $△ A E C$ 和 $△ B F D$ 中， $A E // B F$ ， $A B = C D$ ，添加下列条件仍不能判定 $△ A E C ≌ △ B F D$ 的是（）

A、 $E C // F D$ B、 $A E = B F$ C、 $∠ E = ∠ F$ D、 $E C = F D$

查看试题解析
10. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ，直线MN垂直平分AB交AB于M，交BC于N，且 $∠ B = 15 °$ ， $A C = 2 cm$ ，则BN的长为（）

A、4cm B、3.5cm C、3cm D、4.5cm

查看试题解析
11. 如图，等腰 $△ A B C$ 的底边BC长为4cm，面积为 $16 {cm}^{2}$ ，腰AC的垂直平分线EF交AC于点E，交AB于点F，D为BC的中点，M为直线EF上的动点．则 $△ C D M$ 周长的最小值为（）

A、6cm B、8cm C、9cm D、10cm

查看试题解析
12. 如图，D为△ABC边BC上一点，AB=AC，且BF=CD，CE=BD，则∠EDF等于（）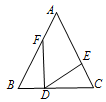

A、90°－∠A B、90°－ $\frac{1}{2}$ ∠A C、180°－∠A D、45°－ $\frac{1}{2}$ ∠A

查看试题解析

二、填空题

13. 要使分式 $\frac{x}{x - 3}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
14. 已知 $a - b = - 1$ ， $a b = 2$ ，则 $(a + 1) (b - 1)$ 的值为．

查看试题解析
15. 如图， $A B = A C$ ， $B D = B C$ ， $A D = D E = E B$ ，则 $∠ A$ 的度数为．

查看试题解析
16. 如图，在 $△ O A B$ 和 $△ O C D$ 中， $O A = O B$ ， $O C = O D$ ， $O A > O C$ ， $∠ A O B = ∠ C O D = 30 °$ 连接AC，BD交于点M，连接OM，下列结论：① $A C = B D$ ；② $∠ C M D = 30 °$ ；③ $O M$ 平分 $∠ C O B$ ；④ $∠ M O A = ∠ M B A$ .正确的结论序号是．

查看试题解析

三、解答题

17.

(1)、因式分解
① $4 m^{2} - 12 m + 9$

② $a^{2} (x - y) + 4 (y - x)$

(2)、先化简，再求值：
$(\frac{x - 1}{x} - \frac{x - 1}{x + 1}) \div \frac{x^{2} - x}{x^{2} + 2 x + 1}$ 其中 $- 2 < x < 3$ 且 $x$ 为整数，请从 $x$ 的以上范围中选一合适的数代入求值．

查看试题解析
18. 如图，平面直角坐标系中 $△ A B C$ 的顶点均在格点上，点 $A$ 的坐标为 $(- 2 ， 3)$ ．

(1)、请在图中作出与 $△ A B C$ 关于 $y$ 轴对称的 $△ A^{'} B^{'} C^{'}$ ；

(2)、写出点 $A^{'} ， B^{'}$ 和点 $C^{'}$ 的坐标．

(3)、求 $△ A B C$ 的面积．

查看试题解析
19. 甲乙两人加工同一种零件，甲每天加工的数量是乙每天加工数量的1.5倍．两人各加工900个这种零件，甲比乙少用5天．

(1)、求甲、乙两人每天各加工多少个这样的零件．

(2)、已知甲、乙两人加工这种零件每天的加工费分别是150元和120元，现有3000个这样的零件加工任务，甲单独加工一段时间后另有安排，剩余任务由乙单独完成．如果总加工费不超过5400元，那么甲至少加工了多少天？

查看试题解析
20. 在等边三角形ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP=∠ACQ，BP=CQ．

(1)、求证：△ABP≌△ACQ；

(2)、请判断△APQ是什么形状的三角形？试说明你的结论．

查看试题解析
21. 已知，如图，在 $△ A B C$ 中， $A D ⊥ B C$ ， $D E = D C$ ，点E是线段AD上一点，且 $B E = A C$ ．

(1)、若 $∠ C = 70 °$ ，求 $∠ A B E$ 的度数；

(2)、判断直线BE与AC的位置关系并证明．

查看试题解析
22. 如图

(1)、方法呈现：
如图①：在 $△ A B C$ 中，若 $A B = 6$ ， $A C = 4$ ，点D为BC边的中点，求BC边上的中线AD的取值范围．

解决此问题可以用如下方法：延长AD到点E使 $D E = A D$ ，再连接BE，可证 $△ A C D ≌ △ E B D$ ，从而把AB、AC， $2 A D$ 集中在 $△ A B E$ 中，利用三角形三边的关系即可判断中线AD的取值范围是，这种解决问题的方法我们称为倍长中线法；

(2)、探究应用：
如图②，在 $△ A B C$ 中，点D是BC的中点， $D E ⊥ D F$ 于点D，DE交AB于点E，DF交AC于点F，连接EF，判断 $B E + C F$ 与EF的大小关系并证明；

(3)、问题拓展：
如图③，在四边形ABCD中， $A B // C D$ ，AF与DC的延长线交于点F、点E是BC的中点，若AE是 $∠ B A F$ 的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．

查看试题解析