山东省日照市岚山区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 某地区开展“二十四节气”标识系统设计活动，以期通过现代设计的手段，尝试推动我国非物质文化遗产创新传承与发展．下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列式子中，为最简二次根式的是（）

A、 $\sqrt{30}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{18}$ D、 $\sqrt{a^{2} b}$

查看试题解析
3. 下列运算结果等于a⁶的是（　　）

A、 $a^{2} + a^{4}$ B、 $a^{2} \cdot a^{3}$ C、 ${(- a^{2})}^{3}$ D、 $a^{8} \div a^{2}$

查看试题解析
4. 如图，有一个正五边形木框，若要保证它不变形，需要再钉的木条根数至少是（）

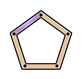A、1 B、2 C、3 D、4

查看试题解析
5. 将一副直角三角板按如图所示的位置放置，两直角三角板各有一条直角边在一条直线上，则∠α的度数是（）

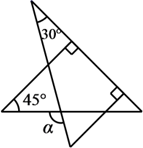A、75° B、90° C、105° D、120°

查看试题解析
6. 如图，在△AOB和△COD中，OA=OC，则下列补充条件中不能说明△AOB≌△COD的是（）

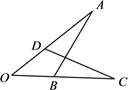A、AB=CD B、OB=OD C、∠A=∠C D、∠ABO=∠CDO

查看试题解析
7. 若某多边形的内角和等于外角和的3倍，则这个多边形的边数是（）

A、6 B、8 C、10 D、12

查看试题解析
8. 估计 $\sqrt{6} \times \sqrt{7} - 1$ 的值应在（）

A、4到5之间 B、5到6之间 C、6到7之间 D、7到8之间

查看试题解析
9. 如图，在△ABC中，DE、FG分别是边AB、AC的垂直平分线，若∠DAF=20°，则∠BAC的度数是（）

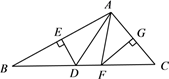A、90° B、100° C、105° D、120°

查看试题解析
10. 若关于x的分式方程 $\frac{m}{x - 2} + \frac{2 x}{2 - x} = 1$ 无解，那么m的值为（）

A、2 B、−2 C、4 D、−4

查看试题解析
11. 如图，在边长为（m+4）的正方形纸片上剪出一个边长为m的小正方形后，将剩余部分剪拼成一个矩形（不重叠无缝隙），若这个矩形的一边长为4，则另一边长是（）

A、m+2 B、m+4 C、2m+2 D、2m+4

查看试题解析
12. 如图，在边长为9的等边△ABC中，CD⊥AB于点D，点E、F分别是边AB、AC上的两个点，且AE=CF=4cm，在CD上有一动点P，则PE+PF的最小值是（）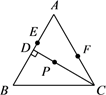

A、4 B、4.5 C、5 D、8

查看试题解析

二、填空题

13. 若式子 $\frac{\sqrt{x} + 1}{x - 1}$ 有意义，则x的取值范围是．

查看试题解析
14. 已知 $a^{m} = 6$ ， $a^{n} = 2$ ，则 $a^{m - n} =$ ．

查看试题解析
15. 在一个三角形中，若其中一个内角的度数是另一个内角的2倍，则我们称这个三角形为“倍角三角形”．已知某“倍角三角形”的一个内角的度数为60°，则其它两个内角的度数分别是．

查看试题解析
16. 如图，△ABC中，∠ABC与∠ACB的平分线交于点D，过点D作EF∥BC，分别交AB、AC于点E、F．那么下列结论：①BD=DC；②△BED和△CFD都是等腰三角形；③点D是EF的中点；④△AEF的周长等于AB与AC的和．其中正确的有．（只填序号）

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{27} - | - 2 \sqrt{3} | - \sqrt{3} \times {(2 - π)}^{0} + {(- 1)}^{2021}$ ．

(2)、先化简，再求值： $(\frac{x}{x - 1} - 1) \div \frac{x^{2} + 2 x + 1}{x^{2} - 1}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
18. 如图，△ABC的三个顶点在边长为1的正方形网格中，已知A（−4，5），B（﹣3，1），C（−2，3）．

⑴画出△ABC及关于y轴对称的△A₁B₁C₁ ，其中点B₁的坐标是 ▲ ；

⑵若点M是x轴上的动点，在图中画出使△B₁CM周长最小时的点M．

查看试题解析
19. 先阅读下列材料，再解答问题：
常用的分解因式的方法有提取公因式法和公式法，但有的多项式只用上述一种方法无法分解，例如多项式 $x^{2} - x y + 4 x - 4 y$ 和 $a^{2} - b^{2} - c^{2} + 2 b c$ ．经过细心观察可以发现，若将多项式进行合理分组后，先将每一组进行分解，分别分解后再用提公因式法或公式法就可以完整分解了.

解答过程如下：
（1） $x^{2} - x y + 4 x - 4 y$

$= (x^{2} - x y) + (4 x - 4 y)$

$= x (x - y) + 4 (x - y)$

$= (x - y) (x + 4)$

（2） $a^{2} - b^{2} - c^{2} + 2 b c$

$= a^{2} - (b^{2} + c^{2} - 2 b c)$

$= a^{2} - {(b - c)}^{2}$

$= (a + b - c) (a - b + c)$

这种方法叫分组分解法，对于超过三项的多项式往往考虑这种方法．利用上述思想方法，把下列各式分解因式：
① $m^{3} - 2 m^{2} - 3 m + 6$
② $x^{2} - 2 x y - 9 + y^{2}$

查看试题解析
20. 如图1是一个平分角的仪器，其中OD=OE，FD=FE．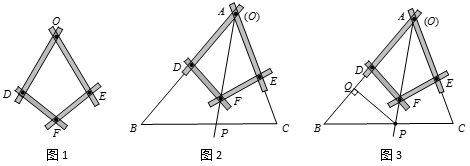

(1)、如图2，将仪器放置在△ABC上，使点O与顶点A重合，D、E分别在边AB、AC上，沿AF画一条射线AP，交BC于点P．则AP就是∠BAC的平分线吗？请给出判断并说明理由．

(2)、如图3，在（1）的前提下，过点P作PQ⊥AB于点Q，已知PQ=4，AC=7，△ABC的面积是32，求AB的长．

查看试题解析
21. 某学校八年级举行数学解题大赛，为表彰获胜的选手，学校准备在商店购买A、B两种文具作为奖品．已知A文具的单价比B文具少8元，且用320元购买A文具的数量与用 480元购买B文具的数量相同．

(1)、求A、B两种文具的单价；

(2)、若学校需要购买A、B两种文具共60件，且购买这两种文具的总费用不超过1200元，则学校至少购买A种文具多少件？

查看试题解析
22. 如图1，在直角△ABC中，∠C=90°，分别作∠CAB的平分线AP和AB的垂直平分线DP，交点为P．

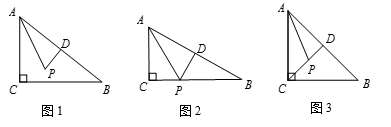(1)、如图2，若点P正好落在BC边上．
①求∠B的度数；

②求证：BC=3PC．

(2)、如图3，若点C、P、D恰好在一条直线上，线段AD、PD、BC之间的数量关系是否满足AD+PD=BC？若满足，请给出证明；若不满足，请说明理由．

查看试题解析