山东省青岛市西海岸区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（）

A、 $- \sqrt{4}$ B、 $3. \overset{\cdot}{1} \overset{\cdot}{4}$ C、 $\frac{1}{3}$ D、 $\sqrt{8}$

查看试题解析
2. 下列句子，是命题的是（）

A、美丽的天空 B、相等的角是对顶角 C、作线段AB=CD D、你喜欢运动吗？

查看试题解析
3. 小明为了解本班同学一周的课外阅读量，随机抽取班上15名同学进行调查，并将调查结果绘制成折线统计图（如图），则下列说法正确的是（）

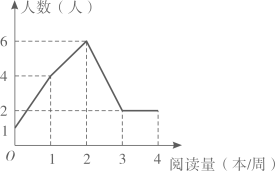A、中位数是3，众数是2 B、众数是1，平均数是2 C、中位数是2，众数是2 D、中位数是3，平均数是2.5

查看试题解析
4. 满足下列条件时， $△ A B C$ 不是直角三角形的是（）

A、 $A B = \sqrt{41}$ ， $B C = 4$ ， $A C = 5$ B、 $A B ： B C ： A C = 3 ： 4 ： 5$ C、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ D、 $∠ A = 40 °$ ， $∠ B = 50 °$

查看试题解析
5. 已知点 $P_{1} (a - 1 ， 5)$ 和 $P_{2} (2 ， b - 1)$ 关于x轴对称，则a+b的值为（）

A、-1 B、0 C、1 D、5

查看试题解析
6. 已知一次函数 $y = k x + 3$ 的图象经过点A，且y随x的增大而减小，则点A的坐标可以是（）

A、 $(- 1 ， 2)$ B、 $(1 ， - 2)$ C、 $(2 ， 3)$ D、 $(3 ， 4)$

查看试题解析
7. 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元购买A，B两种奖品（两种都要买），A种每个15元，B种每个25元，在钱全部用完的情况下，购买方案共有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
8. 已知关于x，y的二元一次方程组 ${\begin{array}{l} y = (7 - k) x - 2 \\ y = (3 k - 1) x + 5 \end{array}$ 无解，则一次函数 $y = k x - \frac{3}{2}$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

二、填空题

9. 比较大小： $\frac{\sqrt{3} - 1}{2}$ $\frac{1}{2}$ （填“＞”“＜”或“＝”）．

查看试题解析
10. 如图，在 $△ A B C$ 中，AB=AC， $∠ A = 40^{\circ}$ ， $C D$ // $A B$ ，则 $∠ B C D$ 的度数是°．

查看试题解析
11. 某 $5$ 人学习小组在寒假期间进行线上测试，其成绩（分）分别为： $86 ， 88 ， 90 ， 92 ， 94$ ，方差为 $s^{2} = 8.0$ ．后来老师发现每人都少加了 $2$ 分，每人补加 $2$ 分后，这 $5$ 人新成绩的方差 $s_{新}^{2} =$ ．

查看试题解析
12. 如图，在一次夏令营活动中，小明从营地A出发，沿北偏东53°方向走了400m到达B点，然后再沿北偏西37°方向走了300m到达目的地C.此时A，C两点之间的距离为m．

查看试题解析
13. 如图，一个正比例函数图象与一次函数y=-x+1的图象相交于点P，则这个正比例函数的表达式是

查看试题解析
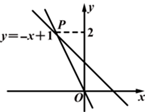14. 如图， $△ A O B$ 与 $△ C O B$ 关于边OB所在的直线成轴对称，AO的延长线交BC于点D.若 $∠ B O D = 46 °$ ， $∠ C = 22 °$ ，则 $∠ A D C =$ °．

查看试题解析
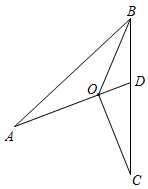15. 如图，是由7块颜色不同的正方形组成的长方形，已知中间小正方形的边长为1，则这个长方形的面积为．

查看试题解析
16. 如图，已知直线 $a$ ： $y = x$ ，直线 $b$ ： $y = - \frac{1}{2} x$ 和点 $P (1 ， 0)$ ，过点 $P$ 作 $y$ 轴的平行线交直线 $a$ 于点 $P_{1}$ ，过点 $P_{1}$ 作 $x$ 轴的平行线交直线 $b$ 于点 $P_{2}$ ，过点 $P_{2}$ 作 $y$ 轴的平行线交直线 $a$ 于点 $P_{3}$ ，过点 $P_{3}$ 作 $x$ 轴的平行线交直线 $b$ 于点 $P_{4}$ ，…，按此作法进行下去，则点 $P_{2021}$ 的横坐标为．

查看试题解析

三、解答题

17.

(1)、计算： $4 - \frac{\sqrt{50} - \sqrt{32}}{\sqrt{8}}$

(2)、计算： $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$

(3)、解方程组： ${\begin{array}{l} 2 x - 5 y = - 21 \\ 4 x + 3 y = 23 \end{array}$

(4)、解方程组： ${\begin{matrix} \frac{x}{3} - y = 4 \\ \frac{x}{4} - y = 1 \end{matrix}$

查看试题解析
18. 如图，直线 $E F$ 分别与直线 $A B$ ， $C D$ 交于点E，F. $E M$ 平分 $∠ B E F$ ， $F N$ 平分 $∠ C F E$ ，且 $E M$ ∥ $F N$ .求证： $A B$ ∥ $C D$ .

查看试题解析
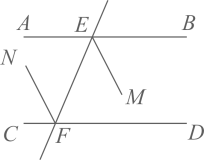19. 为响应“把中国人的饭碗牢牢端在自己手中”的号召，确保粮食安全，优选品种，提高产量，某农业科技小组对A，B两个玉米品种进行了试验种植对比研究．今年A，B两个品种各种植了10亩．收获后A，B两个品种的售价均为2.4元/千克，且B品种的平均亩产量比A品种高100千克，A，B两个品种全部售出后总收入为21600元．求A，B两个品种今年平均亩产量分别是多少千克？

查看试题解析

20. 6月26日是“国际禁毒日”某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动，为了解竞赛情况，从两个年级各抽取10名学生的成绩（满分为100分），收集数据为：七年级90，95，95，80，85，90，85，90，85，100；八年级：85，85，95，80，95，90，90，90，100，90；

整理数据：

	80	85	90	95	100
七年级	2	2	3	2	1
八年级	1	2	4	$a$	1

分析数据：

	平均数	中位数	众数	方差
七年级	89	$b$	90	39
八年级	$c$	90	$d$	30

根据以上信息回答下列问题：

(1)、请直接写出表格中

a ， b ， c ， d

的值

(2)、通过数据分析，你认为哪个年级的成绩比较好？说明理由；

(3)、该校七八年级共600人，本次竞赛成绩不低于90分的为“优秀”估计这两个年级共多少名学生达到“优秀”？

查看试题解析

21. 如图， $B D$ // $G E$ ， $∠ A F G = ∠ 1 = 50 °$ ，AQ平分 $∠ F A C$ ，交BD的延长线于点Q，交DE于点H， $∠ Q = 15 °$ ，求 $∠ C A Q$ 的度数．

查看试题解析
22. 如图1，在A，B两地之间有汽车站C，客车由A地驶往C站，货车由B地驶往A地，两车同时出发，匀速行驶．客车离C站的距离y₁（km）、货车离C站的距离y₂（km）与行驶时间x（h）之间的关系如图2所示．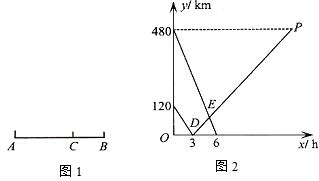

(1)、A，B两地相距千米，货车的速度是千米/时；

(2)、出发3小时后，求货车离C站的距离y₂（km）与行驶时间x（h）之间的关系式；

(3)、两车出发后几小时相遇？

查看试题解析
23. 阅读感悟：
有些关于方程组的问题，需要求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：

已知实数x，y满足 $3 x - y = 5$ ①， $2 x + 3 y = 7$ ②，求 $x - 4 y$ 和 $7 x + 5 y$ 的值．

本题常规思路是将①②两式联立组成方程组，解得x，y的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①-②可得 $x - 4 y = - 2$ ，由①+②×2可得 $7 x + 5 y = 19$ ．这样的解题思想就是通常所说的“整体思想”．解决问题：

(1)、已知二元一次方程组 ${\begin{array}{l} 2 x + 3 y = 17 \\ 3 x + 2 y = 13 \end{array}$ ，则 $x - y =$ ， $x + y =$ ；

(2)、“战疫情，我们在一起”，某公益组织计划为老年公寓捐赠一批防疫物资．已知购买20瓶消毒液、3支测温枪、2套防护服共需1180元；购买30瓶消毒液、2支测温枪、8套防护服共需2170元，若该公益组织实际捐赠了100瓶消毒液、10支测温枪、20套防护服，则购买这批防疫物资共需多少元？

(3)、对于实数x，y，定义新运算： $x * y = a x - b y + c$ ，其中a，b，c是常数，等式右边是通常的加法和乘法运算．已知 $3 * 5 = 15$ ， $4 * 7 = 28$ ，求 $1 * 1$ 的值．

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = x + 2$ 与x轴，y轴分别交于A，B两点，直线 $y = x + 2$ 与直线 $y = n x + 5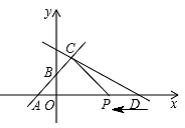$ 相交于点C（m，4） .

(1)、求m，n的值；

(2)、直线 $y = n x + 5$ 与x轴交于点D，动点P从点D开始沿线段DA以每秒1个单位的速度向A点运动，设点P的运动时间为t秒．
①若 $△ A C P$ 的面积为12，求t的值；

②是否存在某一时刻t，使 $△ A C P$ 为等腰三角形？若存在，求出t的值；若不存在，请说明理由．

查看试题解析