山东省青岛市市南区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数中不能作为直角三角形的三边长的是( )

A、1，5， 2， 3 B、7，24，25 C、6，8，10 D、9，12，15

查看试题解析
2. 下列说法错误的是（）

A、 $\frac{4}{9}$ 的平方根是 $\pm \frac{2}{3}$ B、 $\sqrt{25}$ ＝±5 C、 $\sqrt{4}$ 的算术平方根是 $\sqrt{2}$ D、 $\sqrt[3]{- 27}$ ＝﹣3

查看试题解析
3. 若样本x₁ ， x₂ ， x₃ ， …x_n的平均数为18，方差为2，则对于样本x₁+2，x₂+2，x₃+2，…x_n+2，下列结论正确的是（）

A、平均数为20，方差为2 B、平均数为20，方差为4 C、平均数为18，方差为2 D、平均数为18，方差为4

查看试题解析
4. 小涵与阿嘉一起去咖啡店购买同款咖啡豆，咖啡豆每公克的价钱固定，购买时自备容器则结帐金额再减5元.若小涵购买咖啡豆250公克且自备容器，需支付295元；阿嘉购买咖啡豆x公克但没有自备容器，需支付y元，则y与x的关系式为下列何者？（）

A、 $y = \frac{295}{250} x$ B、 $y = \frac{300}{250} x$ C、 $y = \frac{295}{250} x + 5$ D、 $y = \frac{300}{250} x + 5$

查看试题解析
5. 如图，在Rt△ABC中，∠BAC＝90°，点D在BC上，过D作DF⊥BC交BA的延长线于F，连接AD，CF，若∠CFE＝32°，∠ADB＝45°，则∠B的大小是（）

A、32° B、64° C、77° D、87°

查看试题解析
6. 一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行，如图2，当∠BAD＝15°时，BC∥DE，则∠BAD（0°＜∠BAD＜180°）其它所有可能符合条件的度数为（）

A、60°、115°、135° B、45°、60°、105°、135° C、15°、30°、45°、135° D、45°、60°、30°、15°

查看试题解析
7. 如图，在 $R t △ A B O$ 中， $∠ O B A = 90 °$ ， $A (4 ， 4)$ ，点 $C$ 在边 $A B$ 上，且 $\frac{A C}{C B} = \frac{1}{3}$ ，点 $D$ 为 $O B$ 的中点，点 $P$ 为边 $O A$ 上的动点，当点 $P$ 在 $O A$ 上移动时，使四边形 $P D B C$ 周长最小的点 $P$ 的坐标为（）

A、 $(2 ， 2)$ B、 $(\frac{5}{2} ， \frac{5}{2})$ C、 $(\frac{8}{3} ， \frac{8}{3})$ D、 $(3 ， 3)$

查看试题解析
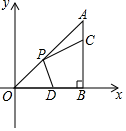8. 如图，△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H．下列结论：①∠DBE＝∠F； ②2∠BEF＝∠BAF＋∠C；③∠F＝∠BAC－∠C；④∠BGH＝∠ABE＋∠C．其中正确个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

9. 如图所示的网格是正方形网格，∠APB＝°．

查看试题解析
10. 某衬衣定价为100元时，每月可卖出2000件，受成本影响，该衬衣需涨价，已知价格每上涨10元，销售量便减少50件.那么，每月售出衬衣的总件数y（件）与衬衣价格x（元）之间的关系式为.

查看试题解析
11. 如果三个数a、b、c满足其中一个数的两倍等于另外两个数的和，我们称这三个数a、b、c是“等差数”若正比例函数y＝2x的图象上有三点A( $\frac{1}{2}$ m﹣1，y₁)、B(m，y₂)、C(2m+1，y₃)，且这三点的纵坐标y₁、y₂、y₃是“等差数”，则m＝．

查看试题解析
12. 魏县鸭梨是我省的特产，经过加工后出售，单价可能提高20%，但重量会减少10%．现有未加工的鸭梨30千克，加工后可以比不加工多卖12元，设加工前每千克卖x元，加工后每千克卖y元，根据题意，可列方程组．

查看试题解析
13. 用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，其阴影部分的面积为．

查看试题解析
14. 某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离y（千米）与货车行驶时间x（小时）之间的函数图象如图所示，现有以下4个结论：①快递车从甲地到乙地的速度为100千米/时；②甲、乙两地之间的距离为120千米； ③图中点B的坐标为（ $3 \frac{3}{4}$ ，75）；④快递车从乙地返回时的速度为90千米/时．以上4个结论中正确的是．

查看试题解析

三、解答题

15. 如图1，图2，图3，图4一个每个小正方形的边长为1正方形网格，借用网格就能计算出一些三角形的面积的面积．

(1)、请你利用正方形网格，计算出如图1所示的△ABC的面积为．

(2)、请你利用正方形网格，在图2中比较 $\sqrt{10} +$ 1与 $\sqrt{13}$ 的大小．

(3)、已知x是正数，请利用正方形网格，在图3中求出 $\sqrt{x^{2} + 9} + \sqrt{{(5 - x)}^{2} + 1}$ 的最小值．

(4)、若△ABC三边的长分别为 $\sqrt{4 m^{2} + n^{2}}$ ， $\sqrt{4 m^{2} + 9 n^{2}}$ ， $\sqrt{16 m^{2} + 4 n^{2}}$ （其中m＞0，n＞0且m≠n），请利用正方形网格，在图4中求出这个三角形的面积．

查看试题解析
16. 计算：

(1)、 $\sqrt{5} \times \sqrt{2} \div 3 \sqrt{5} \times \frac{\sqrt{2}}{2}$ ．

(2)、 $\frac{\sqrt{5} \times \sqrt{21}}{\sqrt{15}} -$ 14 $\sqrt{\frac{1}{7}} - \sqrt[3]{- 8}$ ．

(3)、用含药30%和75%的两种防腐药水，配制含药50%的防腐药水36千克，两种药水各需多少千克？

(4)、甲，乙两位同学在解方程组 ${\begin{array}{l} a x + 3 y = 4 \\ 2 x - b y = - 1 \end{array}$ 时，甲把字母a看错了得到方程组的解为 ${\begin{array}{l} x = 4 \\ y = 3 \end{array}$ ，乙把字母b看错了得到方程组的解为 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ ．求a，b的符合题意值及求原方程组的解．

查看试题解析
17. 如图，∠1+∠2=180°，∠B=∠E，试猜想AB与CE之间有怎样的位置关系？并说明理由．

查看试题解析
18. 随着移动计算技术和无线网络的快速发展，移动学习方式越来越引起人们的关注，某校计划将这种学习方式应用到教育学中，从全校1500名学生中随机抽取了部分学生，对其家庭中拥有的移动设备的情况进行调查，并绘制出如下的统计图①和图②，根据相关信息，解答下列问题：

(1)、本次接受随机抽样调查的学生人数为，图①中m的值为；

(2)、求本次调查获取的样本数据的众数、中位数和平均数；

(3)、根据样本数据，估计该校1500名学生家庭中拥有3台移动设备的学生人数．

查看试题解析
19. 某工厂用如图①所示的长方形和正方形纸板，做成如图②所示的竖式与横式两种长方体的无盖纸盒．现有正方形纸板150张，长方形纸板300张，若这些纸板恰好用完，则可制作横式、竖式两种纸盒各多少个？

查看试题解析
20. 已知，如图，在 $△ A B C$ 中，AD，AE分别是 $△ A B C$ 的高和角平分线，

(1)、若∠B=30°，∠C=50°．求∠DAE的度数；

(2)、试写出∠DAE与∠C，∠B有何关系？并证明你的结论．

查看试题解析
21. 小明从家去李宁体育馆游泳，同时，妈妈从李宁体育馆以50米/分的速度回家，小明到体育馆后发现要下雨，立即返回，追上妈妈后，小明以250米/分的速度回家取伞，立即又以250米/分的速度折回接妈妈，并一同回家．如图是两人离家的距离y（米）与小明出发的时间x（分）之间的函数图象．（注：小明和妈妈始终在同一条笔直的公路上行走，图象上A、C、D、F四点在一条直线上）

(1)、求点C坐标是、BC的函数表达式是．

(2)、求线段OB、AF函数表达式及点D的坐标；

(3)、当x为时，小明与妈妈相距1500米．

查看试题解析
22. 已知某酒店的三人间和双人间客房标价为：三人间为每人每天200元，双人间为每人每天300元，为吸引客源，促进旅游，在“十·一”黄金周期间酒店进行优惠大酬宾，凡团体入住一律五折优惠．一个50人的旅游团在十月二号到该酒店住宿，租住了一些三人间、双人间客房．

(1)、如果租住的每个客房正好住满，并且一天一共花去住宿费6300元．求租住了三人间、双人间客房各多少间？

(2)、设三人间共住了 $x$ 人，这个团一天一共花去住宿费 $y$ 元，请写出 $y$ 与 $x$ 的函数关系式，并写出自变量的取值范围．

(3)、一天6300元的住宿费是否为最低？如果不是，请设计一种方案：要求租住的房间正好被住满的，并使住宿费用最低，请写出设计方案，并求出最低的费用．

查看试题解析
23. （模型定义）
它是由两个共顶点且顶角相等的等腰三角形构成．在相对位置变化的同时，始终存在一对全等三角形．他们得知这种模型称为“手拉手模型”，如果把小等腰三角形的腰长看作是小手，大等腰三角形的腰长看作大手，两个等腰三角形有公共顶点，类似大手拉着小手．

(1)、（模型探究）
如图1，若△ACB和△DCE均为等边三角形，点A、D、E在同一条直线上，连接BE，则∠AEB的度数为；线段BE与AD之间的数量关系是．

(2)、（模型应用）
如图2，AB＝BC，∠ABC＝∠BDC＝60°，求证：AD+CD＝BD；

(3)、如图3，P为等边△ABC内一点，且PA：PB：PC＝3：4：5，以BP为边构造等边△BPM，这样就有两个等边三角形共顶点B，然后连接CM，求∠APB的度数是．

(4)、（拓展提高）
如图4，在△ABC中，AB＝AC，∠BAC＝m°，点E为△ABC外一点，点D为BC中点，∠EBC＝∠ACF，ED⊥FD，求∠EAF的度数．（用含有m的式子表示）

(5)、如图5，两个等腰直角三角形△ABC和△ADE中，AB＝AC，AE＝AD，∠BAC＝∠DAE＝90°，连接BD，CE，两线交于点P，请证明BD和CE的数量关系和位置关系．

(6)、如图6，AD＝4，CD＝3，∠ABC＝∠ACB＝∠ADC＝45°，求BD的长．

(7)、（深化模型）
如图7，C为线段AE上一动点（不与A、E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，以下五个结论：①AD＝BE；②PQ∥AE；③CP＝CQ；④BO＝OE；⑤∠AOB＝60°，恒成立的结论有．

查看试题解析
24. 如图，在平面直角坐标系中，四边形 $O A B C$ 是矩形，点 $O (0 ， 0)$ ，点 $A (3 ， 0)$ ，点 $C (0 ， 4)$ ；D为 $A B$ 边上的动点.

（Ⅰ）如图1，将 $△ A B C$ 对折，使得点B的对应点 $B_{1}$ 落在对角线 $A C$ 上，折痕为 $C D$ ，求此刻点D的坐标；

（Ⅱ）如图2，将 $△ A B C$ 对折，使得点A的与点C重合，折痕交 $A B$ 于点D，交 $A C$ 于点E，求直线 $C D$ 的解析式；

（Ⅲ）在坐标平面内，是否存在点P（除点B外），使得 $△ A P C$ 与 $△ A B C$ 全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析