山东省临沂市罗庄区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下面的图形是用数学家名字命名的,其中轴对称图形的个数是( )
 A、1 B、2 C、3 D、43. 若一个多边形的内角和为1080°,则这个多边形的边数为()
A、1 B、2 C、3 D、43. 若一个多边形的内角和为1080°,则这个多边形的边数为()
A、6 B、7 C、8 D、94. 若 ,则下列分式化简正确的是( )A、 B、 C、 D、5. 分式 的值是零,则 的值为( )A、5 B、-5 C、-2 D、26. 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A、4 B、5 C、6 D、77. 下列多项式中,能运用平方差公式分解因式的是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到 ',那么点B的对应点B'的坐标为( )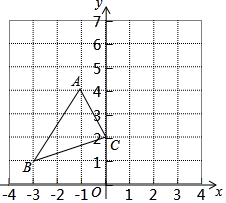 A、(1,7) B、(0,5) C、(3,4) D、(﹣3,2)9. 如图,已知 .能直接判断 的方法是( )
A、(1,7) B、(0,5) C、(3,4) D、(﹣3,2)9. 如图,已知 .能直接判断 的方法是( ) A、 B、 C、 D、10. 已知 .若 ,则x的值为( )A、16 B、8 C、4 D、211. 关于三角形中边与角之间的不等关系,提出如下命题:
A、 B、 C、 D、10. 已知 .若 ,则x的值为( )A、16 B、8 C、4 D、211. 关于三角形中边与角之间的不等关系,提出如下命题:命题1:在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大;
命题2:在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大;
命题3:如果一个三角形中最大的边所对的角是锐角,这个三角形一定是锐角三角形;
命题4:直角三角形中斜边最长;
以上真命题的个数是( )
A、1 B、2 C、3 D、412. 定义:若两个分式的和为n(n为正整数),则称这两个分式互为“n阶分式”.例如,分式 与 互为“3阶分式”.设正数x,y互为倒数,则分式 与 互为( )A、二阶分式 B、三阶分式 C、四阶分式 D、六阶分式二、填空题
-
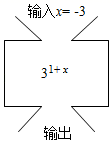
13. 使分式 有意义的x的取值范围是.14. 分解因式: .15. 代数式 与代数式 的值相等,则x= .16. 根据数值转换机的示意图,输出的值为 .
 17. 如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=37°,则∠BAD=度.
17. 如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=37°,则∠BAD=度.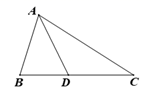 18. 若 ,则19. 如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5 , 且A3A4 B3B4 , 直线l经过B2、B3 , 则直线l与A1A2的夹角α= .
18. 若 ,则19. 如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5 , 且A3A4 B3B4 , 直线l经过B2、B3 , 则直线l与A1A2的夹角α= . 20. 如图,∠AOB=30°,点P在∠AOB的内部,点C,D分别是点P关于OA,OB的对称点,连接CD交OA,OB分别于点E,F;若△PEF的周长的为9,则线段OP=
20. 如图,∠AOB=30°,点P在∠AOB的内部,点C,D分别是点P关于OA,OB的对称点,连接CD交OA,OB分别于点E,F;若△PEF的周长的为9,则线段OP=
三、解答题
-
21.(1)、计算:(2)、分解因式:(3)、解方程:22. 先化简,再求值: ,其中 .23. 如图,△ABC中,AB=AC,∠ABC的平分线BE交AC于D, AF⊥AB交BE于点F.
 (1)、如图1,若∠BAC=40°,求∠AFE的度数;(2)、如图2,若BD⊥AC,垂足为D,BF=8,求DF的长.24. 为切实做好新冠疫情防控工作,我区某校准备在药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.25. 如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)、如图1,若∠BAC=40°,求∠AFE的度数;(2)、如图2,若BD⊥AC,垂足为D,BF=8,求DF的长.24. 为切实做好新冠疫情防控工作,我区某校准备在药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.25. 如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE. (1)、如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°.
(1)、如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°.①求证:AD=BE;
②求∠AEB的度数.
(2)、如图2,若∠ACB=∠DCE=90°,CF为△DCE中DE边上的高,试猜想AE,CF,BE之间的关系,并证明你的结论.26. 在平面直角坐标系中,A(﹣3,0)、B(0,7)、C(7,0),∠ABC+∠ADC=180°,BC⊥CD. (1)、如图1,
(1)、如图1,①求证:∠ABO=∠CAD;
②AB与AD是否相等?请说明理由;
(2)、如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.