山东省临沂市兰山区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下面四个图形分别是可回收垃圾、其它垃圾、厨余垃圾、有害垃圾标志,在这四个标志中,是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 目前世界上刻度最小的标尺是钻石标尺,它的最小刻度为 (其中 ),用科学记数法表示这个最小刻度(单位:m),结果是( )A、 B、 C、 D、3. 一个三角形的两边长分别是2与3,第三边的长不可能为( )A、2 B、3 C、4 D、54. 若 、 的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、5. 若 , ,则 的值为( )A、24 B、81 C、9 D、756. 如图,已知 , 平分 ,若 , ,则 的度数是( )
2. 目前世界上刻度最小的标尺是钻石标尺,它的最小刻度为 (其中 ),用科学记数法表示这个最小刻度(单位:m),结果是( )A、 B、 C、 D、3. 一个三角形的两边长分别是2与3,第三边的长不可能为( )A、2 B、3 C、4 D、54. 若 、 的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、5. 若 , ,则 的值为( )A、24 B、81 C、9 D、756. 如图,已知 , 平分 ,若 , ,则 的度数是( )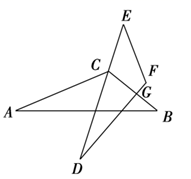 A、30° B、50° C、44° D、34°7. 若关于 的多项式 与 的乘积中,一次项系数为25,则 的值( )A、5 B、-5 C、3 D、-38. 科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
A、30° B、50° C、44° D、34°7. 若关于 的多项式 与 的乘积中,一次项系数为25,则 的值( )A、5 B、-5 C、3 D、-38. 科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( ) A、12米 B、16米 C、18米 D、20米9. 若 是一个完全平方式,则a的值为( )A、20 B、-20 C、±20 D、±1010. 某边防哨卡运来一筐苹果,共有60个,计划每名战士分得数量相同的若干个苹果,结果还剩5个苹果;改为每名战士再多分1个,结果还差6个苹果.若设该哨卡共有 名战士,则所列方程为( )A、 B、 C、 D、11. 如图,在 中, // , 和 的平分线分别交 于点 、 ,若 , ,则 的值为( )
A、12米 B、16米 C、18米 D、20米9. 若 是一个完全平方式,则a的值为( )A、20 B、-20 C、±20 D、±1010. 某边防哨卡运来一筐苹果,共有60个,计划每名战士分得数量相同的若干个苹果,结果还剩5个苹果;改为每名战士再多分1个,结果还差6个苹果.若设该哨卡共有 名战士,则所列方程为( )A、 B、 C、 D、11. 如图,在 中, // , 和 的平分线分别交 于点 、 ,若 , ,则 的值为( )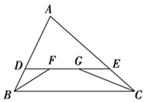 A、3 B、4 C、5 D、912. 如图, , 是 的中点, 平分 ,且 , ,则 的长度为( )
A、3 B、4 C、5 D、912. 如图, , 是 的中点, 平分 ,且 , ,则 的长度为( )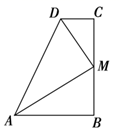 A、 B、 C、 D、13. 如图, , 两点在正方形网格的格点上,每个方格都是边长为1的正方形,点 也在格点上,且 为等腰三角形,在图中所有符合条件的点 的个数为( )
A、 B、 C、 D、13. 如图, , 两点在正方形网格的格点上,每个方格都是边长为1的正方形,点 也在格点上,且 为等腰三角形,在图中所有符合条件的点 的个数为( )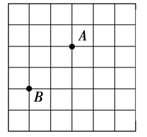 A、7 B、8 C、9 D、1014. 如图,四边形ABCD中, , ,E,F分别是BC,DC上的点,当 的周长最小时, 的度数为( )
A、7 B、8 C、9 D、1014. 如图,四边形ABCD中, , ,E,F分别是BC,DC上的点,当 的周长最小时, 的度数为( )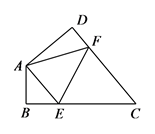 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 计算: .16. 把 分解因式得 .17. 关于 的分式方程 无解,则 的取值是 .18. 在 中, , , , 于 , , 两点分别在边 和射线 上移动.当 , 时, 和 全等.
 19. 读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 ,这里“∑”是求和符号.通过对以上材料的阅读,计算 = .
19. 读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 ,这里“∑”是求和符号.通过对以上材料的阅读,计算 = .三、解答题
-
20. 计算:(1)、 ;(2)、 ;(3)、解分式方程: .21. 已知在平面直角坐标系中有 , , 三点.请回答下列问题:
 (1)、在如图坐标系内画出 关于 轴对称的图形 ,并直接写出各个顶点的坐标;(2)、 与 对应点的坐标的关系是 .(3)、直接写出 的面积: .22. 如图, , , , ,垂足分别为 , , ,求 ,求 的长.
(1)、在如图坐标系内画出 关于 轴对称的图形 ,并直接写出各个顶点的坐标;(2)、 与 对应点的坐标的关系是 .(3)、直接写出 的面积: .22. 如图, , , , ,垂足分别为 , , ,求 ,求 的长. 23. 在今年新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.5元,且用8000元购买A型口罩的数量与用5000元购买B型口罩的数量相同,(1)、A、B两种型号口罩的单价各是多少元?(2)、根据疫情发展情况,该公司还需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3800元,则增加购买A型口罩的数量最多是多少个?
23. 在今年新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.5元,且用8000元购买A型口罩的数量与用5000元购买B型口罩的数量相同,(1)、A、B两种型号口罩的单价各是多少元?(2)、根据疫情发展情况,该公司还需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3800元,则增加购买A型口罩的数量最多是多少个?