山东省聊城市阳谷县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列垃圾分类指引标志图形中，其中是轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 下列各式从左往右变形正确的是（）

A、 $\frac{a + 2}{b + 2} = \frac{a}{b}$ B、 $\frac{a}{b} = \frac{a^{2}}{b^{2}}$ C、 $\frac{a}{b} = \frac{a - 3}{b - 3}$ D、 $\frac{a}{b} = \frac{\frac{1}{3} a}{\frac{1}{3} b}$

查看试题解析
3. 甲，乙，丙，丁四位同学本学期5次50米短跑成绩的平均数 $\bar{x}$ （秒）及方差 $S^{2}$ 如下表所示．若从这四位同学中选出一位成绩较好且状态稳定的同学参加学校比赛，则应该选的同学是（）

甲

乙

丙

丁

$\bar{x}$

7

7

7.5

7.5

$S^{2}$

0.45

0.2

0.2

0.45

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（）

A、15° B、30° C、10° D、20°

查看试题解析
5. 化简 $\frac{a - b}{a} \div (a - \frac{b^{2}}{a})$ 的结果是（）

A、a+b B、a-b C、 $\frac{1}{a + b}$ D、 $\frac{1}{a - b}$

查看试题解析
6. 若点 $P (m - 1, 5)$ 与点 $Q (3, 2 - n)$ 关于 $x$ 轴对称，则 $m + n$ 的值是（）

A、1 B、3 C、5 D、11

查看试题解析
7. “倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为新时期的重要工作.教育主管部门对某学校青年教师2019年度阅读情况进行了问卷调查，并将收集的数据统计如表，根据表中的信息判断，下列结论错误的是（）

A、该学校中青年教师2019年度看书数量的中位数为4本 B、该学校中青年教师2019年平均每人阅读8本书 C、该学校中参与调查的青年教师人数为40人 D、该学校中青年教师2019年度看书数量的众数为4本

查看试题解析
8. 如图，在所给网格中，以格点（网格线的交叉点）A，B的连线为一边构造格点等腰 $△ A B C$ ，则符合条件的点C的个数是（）

A、6 B、7 C、8 D、9

查看试题解析
9. 下列命题中，其逆命题是真命题的是（）

A、对顶角相等 B、两直线平行，同位角相等 C、全等三角形的对应角相等 D、如果 $a = b$ ，那么 $| a | = | b |$

查看试题解析
10. 如图，在已知的△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连接CD，若CD＝AC，∠B＝25°，则∠ACB的度数为（）

A、105° B、100° C、95° D、90°

查看试题解析
11. 小红和小丽分别将9000字和7500字的两篇文稿录入计算机，…，求两人每分钟各录入多少字？设小红每分钟录入x个字，则可得方程 $\frac{9000}{x} = \frac{7500}{220 - x}$ ，根据此情景，题中用“…”表示的缺失的条件应为（）

A、两人每分钟录入字数的和是220字 B、所用时间相同，两人每分钟录入字数的和是220字 C、所用时间相同，小红每分钟录入字数比小丽多220字 D、所用时间相同，小丽每分钟录人字数比小红多200字

查看试题解析
12. 如图，已知△ABC中，AB＝6，BC＝5，AC＝4，∠ABC，∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，连AF，则下列结论：①DE＝BD+CE；②∠BFC＝90°+ $\frac{1}{2}$ ∠ABC；③△ADE的周长为10；④S_△_ABF：S_△_ACF：S_△_BCF＝6：4：5．正确的是（）

A、①③④ B、①②③ C、①②③④ D、②③④

查看试题解析

二、填空题

13. 结合下图，“∵∠B＝60°，AB＝AC，∴△ABC是等边三角形．”在这个推理过程中所使用的几何定理是．

查看试题解析
14. 命题“平行于同一条直线的两条直线平行”的题设是，结论是这两条直线平行，它是命题（填“真”，“假”）．

查看试题解析
15. 数据6，5，x，4，7的平均数是5，那么这组数据的方差为；

查看试题解析
16. 如图，在锐角△ABC中，∠A=80°，DE和DF分别垂直平分边AB、AC，则∠DBC的度数为°．

查看试题解析
17. 若分式方程 $\frac{m}{x - 2} - \frac{2 x}{2 - x} = 1$ 会产生增根，则m的值为.

查看试题解析
18. 如图，三角形纸片ABC中∠A＝75°，∠B＝72°，将三角形纸片的一角折叠，使点C落在△ABC内，如果∠1＝32°，那么∠2＝度．

查看试题解析

三、解答题

19. 先化简，再求值：
$(1 - \frac{4}{x + 1}) \div \frac{x^{2} - 6 x + 9}{x + 1}$ ，其中 $x = - 2$ ．

查看试题解析
20. 已知：如图，点E，F在CD上， $A E // B F$ ， $A E = B F$ ， $C F = D E$ ．求证： $A C // B D$ ．

查看试题解析

21. 2019年12月13日是我国第六个南京大屠杀难者国家公祭日，某校决定开展铭记历史珍爱和平”主题演讲比赛，其中八（1）班要从甲、乙两名参赛选手中择优推荐一人参加校级决赛，他们预赛阶段的各项得分如下表：

项目

选手

演讲内容

演讲技巧

仪表形象

甲

$95$

$90$

$85$

乙

$88$

$92$

$93$

(1)、如果根据三项成绩的平均分确定推荐人选，请通过计算说明甲、乙两人谁会被推荐

(2)、如果根据演讲内容、演讲技、巧仪表形象按

5 : 4 : 1

的比例确定成绩，请通过计算说明甲、乙两人谁会被推荐，并对另外一位同学提出合理的建议．

查看试题解析

22. 解方程

(1)、 $\frac{1}{x - 2} - 3 = \frac{x - 1}{2 - x}$ ；

(2)、 $\frac{4}{x^{2} - 1} = \frac{x + 1}{x - 1} - 1$ ．

查看试题解析
23. 证明：有两个角相等的三角形是等腰三角形.

已知：如图，在 $Δ A B C$ 中， ▲ ，

求证： ▲ .

证明：

查看试题解析
24. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为： $A (1 ， 1)$ ， $B (4 ， 2)$ ， $C (3 ， 4)$ ．

(1)、若 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 关于y轴成轴对称，请在图中作出 $△ A_{1} B_{1} C_{1}$ ，并写出 $△ A_{1} B_{1} C_{1}$ 三个顶点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、若点P为x轴上一点，在图中画出点P，使 $P A + P B$ 的值最小，并直接写出点P的坐标．

查看试题解析
25. 某市为落实“2020脱贫攻坚政策”，工程队计划将该市的1200套老旧房屋进行翻新改造，为尽快完成任务，实际每天翻新改造的数量是原来计划的1.5倍，结果提前20天完成任务，求工程队原计划每天翻新改造老旧房屋的数量．

查看试题解析
26. 如图，AC平分∠BAD，CE⊥AB，CD⊥AD，点E、D为垂足，CF=CB.

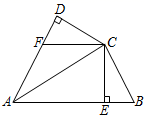(1)、求证：BE=FD；

(2)、若CD=6，AD=8，求四边形ABCF的面积.

查看试题解析
27. 问题情境
如图1， $△ A C B$ 和 $△ D C E$ 均为等边三角形，点A，D，E在同一条直线上，连接BE．

(1)、探究发现
小亮发现： $△ A C D ≌ △ B C E$ ，请你帮他写出推理过程；

(2)、大刚受小亮的启发，求出了 $∠ A E B$ 度数，请直接写出 $∠ A E B$ 等于度；

(3)、小颖在他们两人的基础上又探索出了CD与BE的位置关系为（请直接写出结果）；

(4)、拓展探究
小博士把上面的问题进行了改编：如图2， $△ A C B$ 和 $△ D C E$ 均为等腰直角三角形， $∠ A C B =$ $∠ D C E = 90 °$ ，点A，D，E在同一条直线上，CM为 $△ D C E$ 的边DE上的高，连接BE．试探索CM，AE，BE之间的数量关系，并证明你的结论．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	7	7	7.5	7.5
$S^{2}$	0.45	0.2	0.2	0.45