山东省聊城市莘县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 低碳环保理念深入人心，共享单车已成为出行新方式．下列共享单车图标，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若x、y的值均扩大为原来的2倍，则下列分式的值保持不变的是（）

A、 $\frac{x}{x - y}$ B、 $\frac{2 x}{y^{2}}$ C、 $\frac{x^{2}}{y}$ D、 $\frac{3 x^{3}}{2 y^{2}}$

查看试题解析
3. 用直尺和圆规作一个角的平分线的示意图如图所示，则能说明∠AOC=∠BOC的依据是（）

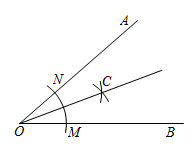A、SSS B、ASA C、AAS D、SAS

查看试题解析
4. 下列各式中最简分式是（）

A、 $\frac{a - b}{b - a}$ B、 $\frac{x^{2} + y^{2}}{x + y}$ C、 $\frac{2 a b}{a^{3}}$ D、 $\frac{x^{2} + 2 x + 1}{1 - x^{2}}$

查看试题解析
5. 如图，已知∠1＝∠2，AC＝AD，增加下列条件：其中不能使△ABC≌△AED的条件（）

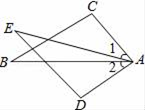A、AB＝AE B、BC＝ED C、∠C＝∠D D、∠B＝∠E

查看试题解析
6. 学校开展为贫困地区捐书活动，以下是5名同学捐书的册数：2，2，x，4，9．已知这组数据的平均数是4，则这组数据的中位数和众数分别是（）

A、2和2 B、4和2 C、2和3 D、3和2

查看试题解析
7. 如图，把一副三角板的两个直角三角形如图叠放在一起，则 $∠ α$ 的度数是（）

A、105° B、115° C、120° D、135°

查看试题解析
8. 下列定理中，逆命题是假命题的是（）

A、在一个三角形中，等角对等边 B、全等三角形对应角相等 C、三边相等的三角形是等边三角形 D、等腰三角形两个底角相等

查看试题解析
9. 若关于x的方程 $\frac{6 - x}{x - 3} - \frac{2 m}{x - 3} = 0$ 有增根，则m的值是（）

A、 $\frac{3}{2}$ B、 $- \frac{2}{3}$ C、3 D、-3

查看试题解析
10. 如图，在 $Δ A B C$ 中，点 $D$ 是边 $A B$ 、 $A C$ 的垂直平分线的交点，已知 $∠ A ＝ 50 °$ ，则 $∠ B D C ＝$ （）

A、180° B、100° C、80° D、50°

查看试题解析
11. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $A C = 12 cm$ ， $B C = 6 cm$ ，一条线段 $P Q = A B$ ， $P$ ， $Q$ 两点分别在线段 $A C$ 和 $A C$ 的垂线 $A X$ 上移动，若以 $A$ 、 $B$ 、 $C$ 为顶点的三角形与以 $A$ 、 $P$ 、 $Q$ 为顶点的三角形全等，则 $A P$ 的值为（）

A、 $6 cm$ B、 $12 cm$ C、 $12 cm$ 或 $6 cm$ D、以上答案都不对

查看试题解析
12. 如图，已知等边 $△ A B C ， A B = 2$ ，点D在 $A B$ 上，点F在 $A C$ 的延长线上， $B D = C F ， D E ⊥ B C$ 于点 $E ， F G ⊥ B C$ 于 $G ， D F$ 交 $B C$ 于点P，则下列结论中：① $B E = C G$ ；② $△ E D P ≌ △ G F P$ ；③ $∠ E D P = 60 °$ ；④ $E P = 1$ ．一定正确的是（）

A、① B、②④ C、①②③ D、①②④

查看试题解析

二、填空题

13. 化简 $\frac{x^{2} - y^{2}}{x - y}$ 的结果为．

查看试题解析
14. 已知一组数据的方差s²= $\frac{1}{4}$ [（x₁﹣6）²+（x₂﹣6）²+（x₃﹣6）²+（x₄﹣6）²]，那么这组数据的总和为．

查看试题解析
15. 如图，已知方格纸中是4个相同的小正方形，则 $∠ 1 + ∠ 2$ 的度数为.

查看试题解析
16. 如图，在△ABC中，AD⊥DE，BE⊥DE，AC、BC分别平分∠BAD和∠ABE．点C在线段DE上．若AD=5，BE=2，则AB的长是．

查看试题解析
17. 已知：①x+ $\frac{2}{x}$ ＝3可转化为x+ $\frac{1 \times 2}{x}$ ＝1+2，解得x₁＝1，x₂＝2，
②x+ $\frac{6}{x}$ ＝5可转化为x+ $\frac{2 \times 3}{x}$ ＝2+3，解得x₁＝2，x₂＝3，

③x+ $\frac{12}{x}$ ＝7可转化为x+ $\frac{3 \times 4}{x}$ ＝3+4，解得x₁＝3，x₂＝4，……

根据以上规律，关于x的方程x+ $\frac{n^{2} + n}{x - 3}$ ＝2n+4的解为．

查看试题解析

三、解答题

18. 先化简， $\frac{x - 2}{x - 1} \div (\frac{3}{x - 1} - x - 1)$ ，然后从 $- 1 ， 1 ， 2$ 中选取一个你喜欢的数作为x的值代入求值．

查看试题解析
19. 解方程： $\frac{x + 1}{x - 2} = \frac{2 x}{x + 3} - 1$ .

查看试题解析
20. 用圆规、直尺作图，不写作法，但要保留作图痕迹，并写出结论．如图，现要在 $△ A B C$ 内建一中心医院，使医院到 $A ， B$ 两个居民小区的距离相等，并且到公路 $A B$ 和 $A C$ 的距离也相等，请确定这个中心医院的位置．

查看试题解析
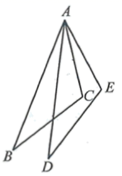
21. 如图，已知 $∠ B A D = ∠ C A E$ ， $A B = A D$ ， $A C = A E$ .
求证： $∠ B = ∠ D$ .

查看试题解析
22. 下表是某校八年级（1）班20名学生某次数学测验的成绩统计表

成绩（分）

60

70

80

90

100

人数（人）

1

5

x

y

2

(1)、若这20名学生成绩的平均分数为82分，求x和y的值；

(2)、在（1）的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求 $a ， b$ 的值．

查看试题解析
23. 列方程或方程组解应用题：
京通公交快速通道开通后，为响应市政府“绿色出行”的号召，家住通州新城的小王上班由自驾车改为乘坐公交车．已知小王家距上班地点18千米．他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米，他从家出发到达上班地点，乘公交车方式所用时间是自驾车方式所用时间的 $\frac{3}{7}$ ．小王用自驾车方式上班平均每小时行驶多少千米？

查看试题解析
24. 如图，在△ABC中，BE是AC边上的高，DE∥BC，∠ADE＝48°，∠C＝62°，求∠ABE的度数.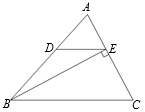

查看试题解析
25. 如图，已知△ABC中，AB=AC=8厘米，BC=6厘米，点D为AB 的中点．如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．当一个点停止运动时，另一个点也随之停止运动．设运动时间为t．

(1)、当点P运动t秒时CP的长度为（用含t的代数式表示）；

(2)、若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；

(3)、若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

查看试题解析

成绩（分）	60	70	80	90	100
人数（人）	1	5	x	y	2