山东省济宁市鱼台县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列代数式 $\frac{2}{x} ， \frac{x + y}{3} ， \frac{1}{2 - a} ， \frac{x}{2 π + 1} ， \frac{x}{b - 3} ， \frac{y}{2} + y$ ，其中属于分式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列等式中从左到右边的变形是分解因式的是（）

A、 $a (a + b - 1) = a^{2} + a b - a$ B、 $a^{2} - a - 2 = a (a - 1) - 1$ C、 $- 4 a^{2} + 9 b^{2} = (- 2 a + 3 b) (2 a + 3 b)$ D、 $2 x + 1 = x (2 + \frac{1}{x})$

查看试题解析
3. 计算 $(- \frac{1}{2} x) \cdot (- 2 x^{2}) (- 4 x^{4})$ 的结果为（）

A、－4x⁶ B、－4x⁷ C、4x⁸ D、－4x⁸

查看试题解析
4. 如果分式 $\frac{x^{2} - 1}{2 x + 1}$ 的值为 $0$ ，则 $x$ 的值是（）

A、1 B、0 C、-1 D、±1

查看试题解析
5. 下列运算正确的是（）

A、 ${(- a^{3})}^{2} = - a^{6}$ B、 $a^{8} \div a^{4} = a^{2}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 ${(- \frac{1}{2})}^{- 2} = 4$

查看试题解析
6. 多项式 $9 x^{2} + 1$ 加上一个单项式后﹐使它成为一个整式的完全平方，那么加上的单项式可以是（）

A、 $\pm 6 x$ B、-1或 $\frac{81}{4} x^{4}$ C、 $- 9 x^{2}$ D、 $\pm 6 x$ 或-1或 $- 9 x^{2}$ 或 $\frac{81}{4} x^{4}$

查看试题解析
7. 若（x+m）（x﹣8）中不含x的一次项，则m的值为（）

A、8 B、﹣8 C、0 D、8或﹣8

查看试题解析
8. 甲乙两港口相距50千米，一艘轮船从甲港口顺流航行至乙港口，又立即从乙港口逆流返回甲港口，共用去8小时，已知水流速度为 $4 k m / h$ ，若设该轮船在静水中的速度为 $x k m / h$ ，则可列方程（）

A、 $\frac{50}{x + 4} + \frac{50}{x - 4} = 8$ B、 $\frac{50}{4 - x} + \frac{50}{4 + x} = 8$ C、 $\frac{100}{4 + x} + \frac{100}{x - 4} = 8$ D、 $\frac{100}{4 - x} + \frac{100}{4 + x} = 8$

查看试题解析
9. 已知 $9 x^{2} - m x y + 16 y^{2}$ 能运用完全平方公式分解因式，则 $m$ 的值为（）

A、12 B、 $\pm 12$ C、24 D、 $\pm 24$

查看试题解析
10. $3 (2^{2} + 1) (2^{4} + 1) (2^{8} + 1)$ ··· $(2^{32} + 1) + 1$ 的个位数是（）

A、4 B、5 C、6 D、8

查看试题解析

二、填空题

11. 当x 时，分式 $\frac{| x | - 1}{x - 1}$ 有意义．

查看试题解析
12. 分式 $\frac{1}{2 x}$ ， $\frac{1}{4 y^{2}}$ ， $-$ $\frac{1}{5 x y}$ 的最简公分母是.

查看试题解析
13. 把多项式 $a^{2} - 4$ 分解因式的结果是．

查看试题解析
14. 已知 $2^{a} = 3$ ， $2^{b} = 6$ ， $2^{c} = 12$ ，则 $a + c - 2 b =$ .

查看试题解析
15. 如图为杨辉三角表，它可以帮助我们按规律写出 ${(a + b)}^{n}$ （其中 $n$ 为正整数）展开式的系数，请仔细观察表中规律，将 ${(a + b)}^{4}$ 的展开式补充完整．
${(a + b)}^{1} = a + b$

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$

${(a + b)}^{4} = a^{4} + 4 a^{3} b +$ $a^{2} b^{2} + 4 a b^{3} + b^{4}$

查看试题解析

三、解答题

16. 计算：

(1)、 $- 6 x^{2} y^{3} \div 2 x^{2} y$

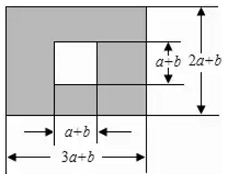
(2)、 $(16 x^{2} y^{3} z + 8 x^{3} y^{2} z) \div 8 x y^{2}$

(3)、运用乘法公式计算： $123^{2} - 124 \times 122$

查看试题解析
17. 因式分解：

(1)、 $8 a^{3} - 2 a$

(2)、 $4 + 12 (x - y) + 9 {(x - y)}^{2}$

查看试题解析
18. 已知 $a^{x} = 2 ， a^{y} = 3$ ，求 $a^{2 x + 3 y}$ 的值

查看试题解析
19. 解分式方程：

(1)、 $\frac{1}{x} + \frac{1}{1.5 x} = \frac{7}{72}$

(2)、 $\frac{x - 2}{x - 3} + \frac{1}{3 - x} = 5$

查看试题解析
20. 已知 $a - b = 7 ， a b = - 12$

(1)、求 $a b^{2} - a^{2} b$ 的值

(2)、求 $a^{2} + b^{2}$ 的值

查看试题解析
21. 如图，某市有一块长为 $(3 a + b)$ 米，宽为 $(2 a + b)$ 米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米?并求出当 $a = 6$ ， $b = 4$ 时的绿化面积．

查看试题解析
22. 某服装店用960元购进一批服装，并以每件46元的价格全部售完，由于服装畅销，服装店又用2220元，再次以比第一次进价多5元的价格购进服装，数量是第一次购进服装的2倍，仍以每件46元的价格出售，卖了部分后，为了加快资金周转，服装店将剩余的20件以售价的九折全部出售.问：

(1)、该服装店第一次购买了此种服装多少件？

(2)、两次出售服装共盈利多少元？

查看试题解析
23. 在当今“互联网＋”时代，有一种用“因式分解法”生成密码的方法：将一个多项式因式分解，如将多项式 $x^{3} - x$ 分解结果为 $x (x + 1) (x - 1)$ ．当 $x = 20$ 时， $x - 1 = 19 ， x + 1 = 21$ ，此时可得到数字密码 $201921$ ，或者是 $192021$

(1)、根据上述方法，当 $x = 16 ， y = 4$ 时，对于多项式． $x^{3} - x y^{2}$ 分解因式后可以形成哪些数字密码（写出两个即可）？

(2)、将多项式 $x^{3} + (m - n) x^{2} + n x$ ．因式分解后﹐利用题目中所示的方法，当 $x = 10$ 时可以得到密码 $101213$ ，求 $m ， n$ 的值．

查看试题解析
24. 我们知道：分式和分数有着很多的相似点.如类比分数的基本性质，我们得到了分式的基本性质；类比分数的运算法则，我们得到了分式的运算法则等等.小学里，把分子比分母小的分数叫做真分数.类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式，
如： $\frac{x + 1}{x - 1} = \frac{x - 1 + 2}{x - 1} = \frac{x - 1}{x - 1} + \frac{2}{x - 1} = 1 + \frac{2}{x - 1}$ ；

$\frac{2 x - 3}{x + 1} = \frac{2 x + 2 - 5}{x + 1} = \frac{2 x + 2}{x + 1} + \frac{- 5}{x + 1} = 2 + (- \frac{5}{x + 1})$ .

(1)、下列分式中，属于真分式的是：（填序号）
① $\frac{a - 2}{a + 1}$ ； ② $\frac{x^{2}}{x + 1}$ ； ③ $\frac{2 b}{b^{2} + 3}$ ； ④ $\frac{a^{2} + 3}{a^{2} - 1}$ .

(2)、将假分式 $\frac{4 a + 3}{2 a - 1}$ 化成整式与真分式的和的形式为：
$\frac{4 a + 3}{2 a - 1}$ =+.

(3)、将假分式 $\frac{a^{2} + 3}{a - 1}$ 化成整式与真分式的和的形式：
$\frac{a^{2} + 3}{a - 1}$ =+.

查看试题解析