山东省济宁市兖州区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 若一个三角形的两边长分别为3 、6 ,则它的第三边的长可能是( )A、2 B、3 C、6 D、92. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 打喷嚏 捂口鼻
B、
打喷嚏 捂口鼻
B、 勤洗手 勤通风
C、
勤洗手 勤通风
C、 戴口罩 讲卫生
D、
戴口罩 讲卫生
D、 喷嚏后 慎揉眼
3. 如果把分式 中的 和 都扩大2倍,那么分式的值( )A、扩大3倍 B、扩大9倍 C、缩小3倍 D、不变4. 下列计算正确的是( )A、 B、 C、 D、5. 在 中, , 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )
喷嚏后 慎揉眼
3. 如果把分式 中的 和 都扩大2倍,那么分式的值( )A、扩大3倍 B、扩大9倍 C、缩小3倍 D、不变4. 下列计算正确的是( )A、 B、 C、 D、5. 在 中, , 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( ) A、3 B、 C、2 D、66. 如图,已知E,B,F,C四点在一条直线上, , ,添加以下条件之一,仍不能证明 ≌ 的是
A、3 B、 C、2 D、66. 如图,已知E,B,F,C四点在一条直线上, , ,添加以下条件之一,仍不能证明 ≌ 的是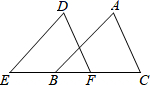 A、 B、 C、 D、7. 甲、乙两人做某种机械零件,已知甲做240个零件与乙做280个零件所用的时间相等,两人每天共做130个零件.设甲每天做x个零件,下列方程正确的是( )A、 B、 C、 D、8. 利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2 . 你根据图乙能得到的数学公式是( )
A、 B、 C、 D、7. 甲、乙两人做某种机械零件,已知甲做240个零件与乙做280个零件所用的时间相等,两人每天共做130个零件.设甲每天做x个零件,下列方程正确的是( )A、 B、 C、 D、8. 利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2 . 你根据图乙能得到的数学公式是( ) A、(a+b)(a﹣b)=a2﹣b2 B、(a﹣b)2=a2﹣2ab+b2 C、a(a+b)=a2+ab D、a(a﹣b)=a2﹣ab9. 如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )
A、(a+b)(a﹣b)=a2﹣b2 B、(a﹣b)2=a2﹣2ab+b2 C、a(a+b)=a2+ab D、a(a﹣b)=a2﹣ab9. 如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )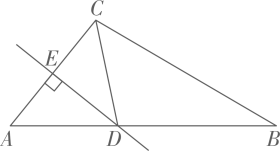 A、 B、 C、 D、10. 如图, 中, , , , 为 的中点,若动点 以 的速度从 点出发,沿 的方向运动,设 点的运动时间为 秒 ,连接 ,当 是直角三角形时, 的值为( )
A、 B、 C、 D、10. 如图, 中, , , , 为 的中点,若动点 以 的速度从 点出发,沿 的方向运动,设 点的运动时间为 秒 ,连接 ,当 是直角三角形时, 的值为( ) A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5二、填空题
-
11. 若代数式 有意义,则实数x的取值范围是 .12. 因式分解: .13. 一个 边形的内角和等于外角和的2倍,则其边数 为 .14. 如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是 .
 15. 某中学假期后勤中的一项工作是请 名木工制作200把椅子和100张课桌,已知一名工人在单位时间内可以制作10把椅子或7张课桌,将这30名工人分成两组,一组制作课桌,一组制作椅子,两组同时开工.应分配人制作课桌,才能使完成此项工作的时间最短.
15. 某中学假期后勤中的一项工作是请 名木工制作200把椅子和100张课桌,已知一名工人在单位时间内可以制作10把椅子或7张课桌,将这30名工人分成两组,一组制作课桌,一组制作椅子,两组同时开工.应分配人制作课桌,才能使完成此项工作的时间最短.三、解答题
-
16. 已知:如图点D在AB上,E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C,求证:BD=CE.
 17. 计算:(1)、 ;(2)、先化简 ,再从 中选择合适的 值代入求值.(3)、如图,一块直径为a+b的圆形钢板,从中挖去直径为 与 的两个圆.
17. 计算:(1)、 ;(2)、先化简 ,再从 中选择合适的 值代入求值.(3)、如图,一块直径为a+b的圆形钢板,从中挖去直径为 与 的两个圆.①用含有 的代数式来表示剩下钢板的面积;
②当 时,剩下的钢板的面积为多少?
 18. 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形(请画出图形,写出已知、求证、证明的过程).19. 给出下列算式: ;
18. 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形(请画出图形,写出已知、求证、证明的过程).19. 给出下列算式: ;;
;
.
······
(1)、观察上面一系列式子,你能发现什么规律?(2)、用含 为正整数)的式子表示出来你发现的规律,并证明这个规律﹔(3)、计算 , 此时 .20. 如图, 中, 点 是直线 上的一动点(不和 重合), 交 所在的直线于点 交直线 于 . (1)、点 在边 上时,证明: ;(2)、点 在 的延长线或反向延长线上时, 中的结论是否成立?若成立,请给出证明;若不成立,请画出图形,并直接写出 三者之间数量关系.21. 中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开.某茶店用4000元购进了A种茶叶若干盒,用8400元购进B种茶叶若干盒,所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍.(1)、A , B两种茶叶每盒进价分别为多少元?(2)、第一次所购茶叶全部售完后第二次购进A , B两种茶叶共100盒(进价不变),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元.两种茶叶各售出一半后,为庆祝国际茶日,两种茶叶均打七折销售,全部售出后,第二次所购茶叶的利润为5800元(不考虑其他因素),求本次购进A , B两种茶叶各多少盒?22. 如图
(1)、点 在边 上时,证明: ;(2)、点 在 的延长线或反向延长线上时, 中的结论是否成立?若成立,请给出证明;若不成立,请画出图形,并直接写出 三者之间数量关系.21. 中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开.某茶店用4000元购进了A种茶叶若干盒,用8400元购进B种茶叶若干盒,所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍.(1)、A , B两种茶叶每盒进价分别为多少元?(2)、第一次所购茶叶全部售完后第二次购进A , B两种茶叶共100盒(进价不变),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元.两种茶叶各售出一半后,为庆祝国际茶日,两种茶叶均打七折销售,全部售出后,第二次所购茶叶的利润为5800元(不考虑其他因素),求本次购进A , B两种茶叶各多少盒?22. 如图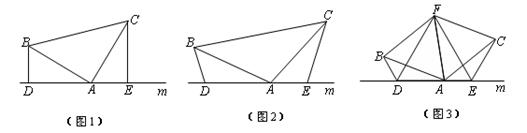 (1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.