山东省济宁市泗水县2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列四个图形中,是轴对称图形的有( )
 A、4个 B、3个 C、2个 D、1个2. 下列计算中,正确的是( )A、 B、 C、 D、3. 下列各式由左边到右边的变形中,是分解因式的为( )A、 B、 C、 D、4. 已知 , ,则 的值为( )
A、4个 B、3个 C、2个 D、1个2. 下列计算中,正确的是( )A、 B、 C、 D、3. 下列各式由左边到右边的变形中,是分解因式的为( )A、 B、 C、 D、4. 已知 , ,则 的值为( )
A、9 B、 C、12 D、5. 下列各式中能用完全平方公式法分解因式的是( )A、 B、 C、 D、6. 下列各式中,相等关系一定成立的是( )A、 B、 C、 D、7. 若分式 的值为0,则x的值为( )A、4 B、-4 C、3或-3 D、38. 下列运算中正确的是( )A、 B、 C、 D、9. 如图, 相交于点 ,则下列说法中正确的个数是( )① ;②点 到 的距离相等;③ ;④
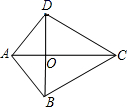 A、4 B、3 C、2 D、110. 如图,等边 中, 于 点 分别为上 的两个定点且 ,在 上有一动点 使 最短,则 的最小值为( )
A、4 B、3 C、2 D、110. 如图,等边 中, 于 点 分别为上 的两个定点且 ,在 上有一动点 使 最短,则 的最小值为( ) A、3.5 B、4 C、5 D、611. 如图,在 中, ,以 为圆心,任意长为半径画弧分别交 于点 和 ,再分别以 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 ,并延长交 于点 ,则下列说法中正确的个数是( )
A、3.5 B、4 C、5 D、611. 如图,在 中, ,以 为圆心,任意长为半径画弧分别交 于点 和 ,再分别以 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 ,并延长交 于点 ,则下列说法中正确的个数是( )
① 是 的平分线;② ;③点 在 的垂直平分线上;④若 ,则点 到 的距离是 ,
A、2 B、3 C、4 D、512. 在矩形 内将两张边长分别为 和 的正方形纸片按图1和图2两种方式放置(图1和图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为 ,图2中阴影部分的面积为 .当 时, 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 点 关于y轴对称的点的坐标是 .14. 分解因式:15. 如图,把等腰直角三角板放平面直角坐标系内,已知直角顶点 的坐标为 ,另一个顶点 的坐标为 ,则点 的坐标为
 16. 如图,一个直角三角形纸板的直角边 分别经过正八边形的两个顶点,则图中
16. 如图,一个直角三角形纸板的直角边 分别经过正八边形的两个顶点,则图中 17. 在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生密码,方便记忆.原理是:如对于多项式 ,因式分解的结果是 ,若取 时,则各个因式的值是: ,于是就可以把“ ”作为一个六位数的密码.对于多项式 ,取 时,用上述方法产生的密码是:(写出一个即可).18. 在平面直角坐标系中,若干个边长为 个单位长度的等边三角形,按如图中的规律摆放.点 从原点 出发,以每秒 个单位长度的速度沿着等边三角形的边“ …”的路线运动,设第 秒运动到点 ,( 为正整数),则点 的坐标是
17. 在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生密码,方便记忆.原理是:如对于多项式 ,因式分解的结果是 ,若取 时,则各个因式的值是: ,于是就可以把“ ”作为一个六位数的密码.对于多项式 ,取 时,用上述方法产生的密码是:(写出一个即可).18. 在平面直角坐标系中,若干个边长为 个单位长度的等边三角形,按如图中的规律摆放.点 从原点 出发,以每秒 个单位长度的速度沿着等边三角形的边“ …”的路线运动,设第 秒运动到点 ,( 为正整数),则点 的坐标是
三、解答题
-
19.(1)、(2)、20. 先化简,再求值: ,其中21. 如图,点D在△ABC的AB边上,且∠ACD=∠A.
 (1)、作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,判断直线DE与直线AC的位置关系,并说明理由.22. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形) 的顶点 的坐标分别为
(1)、作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,判断直线DE与直线AC的位置关系,并说明理由.22. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形) 的顶点 的坐标分别为 (1)、请在如图所示的网格内作出平面直角坐标系并作出 关于 轴对称的(2)、写出点 的坐标并求出 的面积.23. 如图,在正方形中 , 是 上一点, 是 延长线上一点,且 .
(1)、请在如图所示的网格内作出平面直角坐标系并作出 关于 轴对称的(2)、写出点 的坐标并求出 的面积.23. 如图,在正方形中 , 是 上一点, 是 延长线上一点,且 . (1)、求证: ;(2)、若点 在 上,且 ,判断线段 之间的数量关系,并说明理由.24. 某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.(1)、求甲、乙两种商品的每件进价;(2)、该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元.销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?25. 如图
(1)、求证: ;(2)、若点 在 上,且 ,判断线段 之间的数量关系,并说明理由.24. 某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.(1)、求甲、乙两种商品的每件进价;(2)、该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元.销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?25. 如图

我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图(1)可以用来解释 ,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.
如图(2),将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为 的大正方形,两块是边长都为 的小正方形,五块是长为 ,宽为 的全等小长方形,且 .(以上长度单位: )
(1)、观察图形,可以发现代数式 可以分解因式为(2)、若每块小长方形的面积为 ,四个正方形的面积和为 试求图中所有裁剪线(虚线部分)长之和.26. 如图,以直角三角形AOC的直角顶点O为原点,以OC,OA所在直线为轴和轴建立平面直角坐标系,点A(0,a),C(b,0)满足 . (1)、a=;b=;直角三角形AOC的面积为 .(2)、已知坐标轴上有两动点P,Q同时出发,P点从C点出发以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发以每秒1个单位长度的速度向点A匀速移动,点P到达O点整个运动随之结束.AC的中点D的坐标是(4,3),设运动时间为t秒.问:是否存在这样的t,使得△ODP与△ODQ的面积相等?若存在,请求出t的值;若不存在,请说明理由.(3)、在(2)的条件下,若∠DOC=∠DCO,点G是第二象限中一点,并且y轴平分∠GOD.点E是线段OA上一动点,连接接CE交OD于点H,当点E在线段OA上运动的过程中,探究∠GOD,∠OHC,∠ACE之间的数量关系,并证明你的结论(三角形的内角和为180).
(1)、a=;b=;直角三角形AOC的面积为 .(2)、已知坐标轴上有两动点P,Q同时出发,P点从C点出发以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发以每秒1个单位长度的速度向点A匀速移动,点P到达O点整个运动随之结束.AC的中点D的坐标是(4,3),设运动时间为t秒.问:是否存在这样的t,使得△ODP与△ODQ的面积相等?若存在,请求出t的值;若不存在,请说明理由.(3)、在(2)的条件下,若∠DOC=∠DCO,点G是第二象限中一点,并且y轴平分∠GOD.点E是线段OA上一动点,连接接CE交OD于点H,当点E在线段OA上运动的过程中,探究∠GOD,∠OHC,∠ACE之间的数量关系,并证明你的结论(三角形的内角和为180).