山东省济南市济阳区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 16的算术平方根是( )A、4 B、±4 C、8 D、±82. 在平面直角坐标系中,下列各点位于第二象限的点是( )A、(3,2) B、(﹣3,﹣2) C、(3,﹣2) D、(﹣3,2)3. 如图,直线AB∥CD,直线EF分别与直线AB、CD相交于点G、H,若∠2=35°,则∠1 的度数为( )
 A、165° B、155° C、145° D、135°4. 如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向下平移3个单位长度,再向右平移2个单位长度,得到 △A1B1C1 , 那么点A的对应点A1的坐标为( )
A、165° B、155° C、145° D、135°4. 如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向下平移3个单位长度,再向右平移2个单位长度,得到 △A1B1C1 , 那么点A的对应点A1的坐标为( ) A、(0,2) B、(0,-2) C、(2,0) D、(-2,0)5. 下列命题中,是假命题的是( )A、直角三角形的两个锐角互余 B、在同一个平面内,垂直于同一条直线的两条直线平行 C、同旁内角互补,两直线平行 D、三角形的一个外角大于任何一个内角6. 已知 二元一次方程2x+my=5的一组解,则m的值是( )A、 B、 C、 D、7. 已知点(x1 , y1),(x1+1,y2)都在直线y=-3x+2上,则y1 与y2的大小关系是( )A、y1 >y2 B、y1 =y2 C、y1 <y2 D、不能比较8. 某校八(3)班40名同学为“希望工程”捐款,共捐款510元,捐款情况如下表:
A、(0,2) B、(0,-2) C、(2,0) D、(-2,0)5. 下列命题中,是假命题的是( )A、直角三角形的两个锐角互余 B、在同一个平面内,垂直于同一条直线的两条直线平行 C、同旁内角互补,两直线平行 D、三角形的一个外角大于任何一个内角6. 已知 二元一次方程2x+my=5的一组解,则m的值是( )A、 B、 C、 D、7. 已知点(x1 , y1),(x1+1,y2)都在直线y=-3x+2上,则y1 与y2的大小关系是( )A、y1 >y2 B、y1 =y2 C、y1 <y2 D、不能比较8. 某校八(3)班40名同学为“希望工程”捐款,共捐款510元,捐款情况如下表:
表格中捐款6元和8元的人数不小心被墨水污染已看不清楚。若设捐款6元的有x名同学,捐款8元的有y名同学,根据题意,可得方程组( )
A、 B、 C、 D、9. 将一副三角尺按如图所示的方式摆放,则 的大小为( ) A、 B、 C、 D、10. “元旦”期间,老李一家自驾游去了离家320千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A、 B、 C、 D、10. “元旦”期间,老李一家自驾游去了离家320千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( ) A、1.25小时 B、4小时 C、4.25小时 D、4.75小时11. 如图,在△ABC中,∠ACB=90°,D在AB上,将△ABC沿CD折叠,点B落在AC边上的点B′处,若 ,则∠A的度数为( )
A、1.25小时 B、4小时 C、4.25小时 D、4.75小时11. 如图,在△ABC中,∠ACB=90°,D在AB上,将△ABC沿CD折叠,点B落在AC边上的点B′处,若 ,则∠A的度数为( ) A、25° B、30° C、35° D、40°12. 定义新运算:对于任意实数a,b都有a※b=am-bn,等式右边是通常的减法和乘法运算.规定,若3※2=5,1※(-2)=-1,则(-3)※1的值为( )A、-2 B、-4 C、-7 D、-11
A、25° B、30° C、35° D、40°12. 定义新运算:对于任意实数a,b都有a※b=am-bn,等式右边是通常的减法和乘法运算.规定,若3※2=5,1※(-2)=-1,则(-3)※1的值为( )A、-2 B、-4 C、-7 D、-11二、填空题
-
13. 计算 的结果是 .14. 如图,△ABC中AD⊥BC于D,AC=2, DC=1,BD=3, 则AB的长为 .
 15. 某中学规定学生体育成绩满分为100分,按课外活动成绩、期中成绩、期末成绩2:3:5的比计算学期成绩.小明同学本学期三项成绩依次为90分、80分、90分,则小明同学本学期的体育成绩是分.16. 已知 是方程组 的解,则数据3,a,1,b,4的方差为 .17. 如图,在平面直角坐标系xOy中,一次函数 与正比例函数 的图象交于点 ,与x轴交于点B(5,0),则△OAB的面积是 .
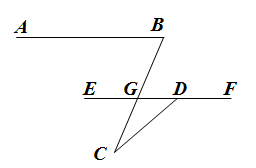
15. 某中学规定学生体育成绩满分为100分,按课外活动成绩、期中成绩、期末成绩2:3:5的比计算学期成绩.小明同学本学期三项成绩依次为90分、80分、90分,则小明同学本学期的体育成绩是分.16. 已知 是方程组 的解,则数据3,a,1,b,4的方差为 .17. 如图,在平面直角坐标系xOy中,一次函数 与正比例函数 的图象交于点 ,与x轴交于点B(5,0),则△OAB的面积是 . 18. 如图,BF平分∠ABD,CE平分∠ACD,BF与CE交于G,若 ,则∠A的度数为 .
18. 如图,BF平分∠ABD,CE平分∠ACD,BF与CE交于G,若 ,则∠A的度数为 .
三、解答题
-
19. 计算:20. 解方程组:21. 已知:如图, ,求∠BCD的度数.
 22. 如图,网格中小正方形的边长为1,
22. 如图,网格中小正方形的边长为1, (1)、画出△ABC关于x轴对称的△A1B1C1(其中A1、B1、C1分别为A、B、C的对应点);(2)、△ABC的面积为;点B到边AC的距离为;(3)、在x轴上是否存在一点M,使得MA+MB最小,若存在,请直接写出MA+MB的最小值;若不存在,请说明原因23. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
(1)、画出△ABC关于x轴对称的△A1B1C1(其中A1、B1、C1分别为A、B、C的对应点);(2)、△ABC的面积为;点B到边AC的距离为;(3)、在x轴上是否存在一点M,使得MA+MB最小,若存在,请直接写出MA+MB的最小值;若不存在,请说明原因23. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).

信息二:第三组的成绩(单位:分)为74 71 73 74 79 76 77 76 76 73 72 75
根据信息解答下列问题:
(1)、补全第二组频数分布直方图(直接在图中补全);(2)、第三组竞赛成绩的众数是分,抽取的50名学生竞赛成绩的中位数是分;(3)、若该校共有1500名学生参赛,请估计该校参赛学生成绩不低于80分的约为人.24. 为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:时间
销售数量(个)
销售收入(元)(销售收入=售价×销售数量)
甲种型号
乙种型号
第一月
22
8
1100
第二月
38
24
2460
(1)、求甲、乙两种型号水杯的售价;(2)、第三月超市计划再购进甲、乙两种型号水杯共80个,设购进甲种型号水杯a个,在 80个水杯全部售完的情况下,利润为w元,写出w与a的函数关系式.(不用写出a 的取值范围)25. 甲、乙两车同时从A地出发,沿同一路线赶往距离A地800km的B地,在行驶过程中乙车速度始终保持80km/h,甲车先以一定速度行驶了500km,用时5h,然后再以乙车的速度行驶,直至到B地(加油、休息时间忽略不计).甲、乙两车离A地的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题: (1)、甲车改变速度前的速度是km/h,甲车行驶h到达B地,乙车行驶h到达B地;(2)、求甲车改变速度后离A地的路程y(km)与所用时间x(h)之间的函数解析式(不用写出自变量x的取值范围);(3)、出发h时,甲、乙两车相距40km.26. △ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)、甲车改变速度前的速度是km/h,甲车行驶h到达B地,乙车行驶h到达B地;(2)、求甲车改变速度后离A地的路程y(km)与所用时间x(h)之间的函数解析式(不用写出自变量x的取值范围);(3)、出发h时,甲、乙两车相距40km.26. △ABC中,AD是∠BAC的角平分线,AE是△ABC的高. (1)、如图1,若∠B=40°,∠C=60°,求∠DAE的度数;(2)、如图2,∠B<∠C,则DAE、∠B,∠C之间的数量关系为;(3)、如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.27. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)、如图1,若∠B=40°,∠C=60°,求∠DAE的度数;(2)、如图2,∠B<∠C,则DAE、∠B,∠C之间的数量关系为;(3)、如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.27. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.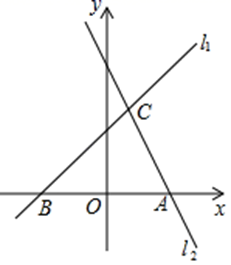 (1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.(3)、在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.(3)、在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.