山东省济南市槐荫区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 在 中,无理数是( )A、0 B、-5 C、0.14 D、2. 下列四组数中,是勾股数的是( )A、 B、 C、 D、3. 一次函数y=﹣2x+2的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 某射击运动员在一次射击练习中,成绩(单位:环)记录如下:8,9,8,7,10.这组数据的平均数和中位数分别是( )A、8,8 B、8.4,8 C、8.4,8.4 D、8,8.45. 如图,表示 的点落在( )
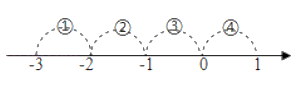 A、段① B、段② C、段③ D、段④6. 下列图形中,不能代表y是x函数的是( )A、
A、段① B、段② C、段③ D、段④6. 下列图形中,不能代表y是x函数的是( )A、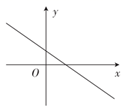 B、
B、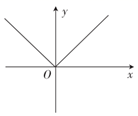 C、
C、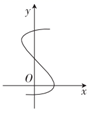 D、
D、 7. 已知 ,则下列结论不成立的是( )A、 B、 C、 D、8. 如图,直线 经过点 ,则关于 的不等式 的解集是( )
7. 已知 ,则下列结论不成立的是( )A、 B、 C、 D、8. 如图,直线 经过点 ,则关于 的不等式 的解集是( )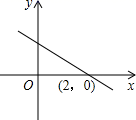 A、x>2 B、x<2 C、x≥2 D、x≤29. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是点A(-3,0)、点B(-1,2)、点C(3,2).则到△ABC三个顶点距离相等的点的坐标是( )
A、x>2 B、x<2 C、x≥2 D、x≤29. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是点A(-3,0)、点B(-1,2)、点C(3,2).则到△ABC三个顶点距离相等的点的坐标是( )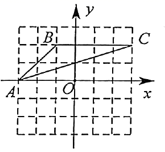 A、(0,-1) B、(0,0) C、(1,-1) D、(1,-2)10. 如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
A、(0,-1) B、(0,0) C、(1,-1) D、(1,-2)10. 如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( ) A、2个 B、3个 C、4个 D、5个11. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 ,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是( )
A、2个 B、3个 C、4个 D、5个11. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 ,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是( ) A、 寸 B、 寸 C、 寸 D、 寸12. 如图,长方形 的各边分别平行于 轴或 轴,物体甲和物体乙分别由点 同时出发,沿矩形 的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2021次相遇地点的坐标是( )
A、 寸 B、 寸 C、 寸 D、 寸12. 如图,长方形 的各边分别平行于 轴或 轴,物体甲和物体乙分别由点 同时出发,沿矩形 的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2021次相遇地点的坐标是( )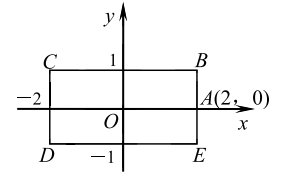 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 在平面直角坐标系中,点P(-3,-5)关于x轴对称的点的坐标是.14. 不等式 的解集是 .15. 甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.5米,方差分别为s甲2=0.2,S乙2=0.08,成绩比较稳定的是(填“甲”或“乙”).16. 等腰三角形中,若一个角是 ,则它的顶角的度数为 .17. 如图所示,在 中, 垂直平分 ,交 于点 ,垂足为点 , ,则 的长为 .
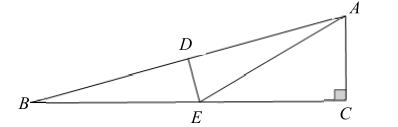 18. 如图,在平面直角坐标系中,△ABO的边OB在x轴上,∠OBA=90°,∠AOB=30°,AB=3,点C是边AB的中点,点D在边OB上,且OD= ,点P为边OA上的动点,当四边形PDBC周长最小时,点P的横坐标为 .
18. 如图,在平面直角坐标系中,△ABO的边OB在x轴上,∠OBA=90°,∠AOB=30°,AB=3,点C是边AB的中点,点D在边OB上,且OD= ,点P为边OA上的动点,当四边形PDBC周长最小时,点P的横坐标为 .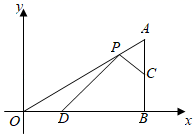
三、解答题
-
19. 计算(1)、(2)、20. 求不等式组 的整数解.21. 如图,正方形网格中的每个小正方形边长都是1.(1)、在图1中,画一个顶点为格点、面积为2的正方形;
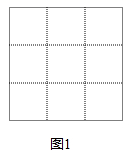 (2)、在图2中,仅用直尺,找一格点 ,满足以下两个条件:
(2)、在图2中,仅用直尺,找一格点 ,满足以下两个条件: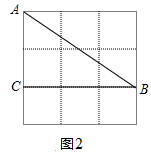
①点 到 的距离相等;
②点 到点 的距离相等.(保留作图痕迹)
22. 如图,在△ABC中,AB=AC,BD平分∠ABC,CE平分∠ACB,过点A分别作BD、CE的垂线段AD、AE,垂足为D、E,求证:AD=AE.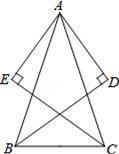 23. 如图,在平面直角坐标系中,点 ,点 分别在 轴, 轴的正半轴上,且满足 .
23. 如图,在平面直角坐标系中,点 ,点 分别在 轴, 轴的正半轴上,且满足 . (1)、求点 的坐标及直线 的解析式;(2)、在 轴上是否存在点 ,使以点 为顶点的三角形的面积 ?若存在,请写出点 的坐标;若不存在,请说明理由.24. 某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图统计图.
(1)、求点 的坐标及直线 的解析式;(2)、在 轴上是否存在点 ,使以点 为顶点的三角形的面积 ?若存在,请写出点 的坐标;若不存在,请说明理由.24. 某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图统计图.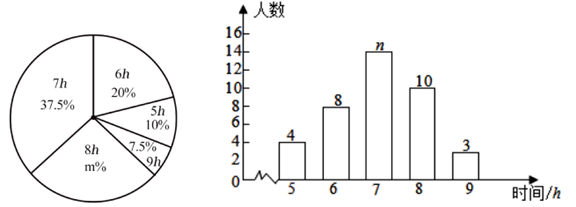
请根据相关信息,解答下列问题:
(1)、本次接受调查的初中学生人数为人,扇形统计图中的 ;(2)、所调查的初中学生每天睡眠时间的众数是 , 平均数是;(3)、该校共有 名初中学生,根据样本数据,估计该校初中学生每天睡眠时间不足 小时的人数.25. 今年冬天受寒潮影响,淘宝上的电热取暖器销售火爆.某电商销售每台成本价分别为200元、170元的A、B两种型号的电热取暖器,下表是近两天的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一天
3台
5台
1800元
第二天
4台
10台
3100元
(1)、求A、B两种型号的电热取暖器的销售单价;(2)、若该电商准备用不多于5400元的金额再采购这两种型号的电热取暖器共30台,问A种型号的电热取暖器最多能采购多少台?26. 快车与慢车分别从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时间x(h)的关系如图所示.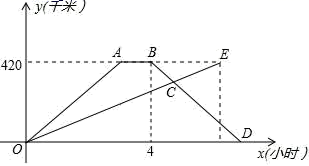 (1)、甲乙两地之间的路程为km;快车的速度为km/h;慢车的速度为km/h;(2)、出发h,快慢两车距各自出发地的路程相等;(写出解答过程快慢两车出发h相距150km.(写出解答过程)27. 如图
(1)、甲乙两地之间的路程为km;快车的速度为km/h;慢车的速度为km/h;(2)、出发h,快慢两车距各自出发地的路程相等;(写出解答过程快慢两车出发h相距150km.(写出解答过程)27. 如图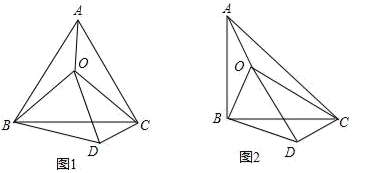 (1)、如图1, 是等边 内一点,连接 ,且 ,连接 .
(1)、如图1, 是等边 内一点,连接 ,且 ,连接 .① ▲ 度;(答案直接填写在横线上)
② ▲ ﹔(答案直接填写在横线上)
③求 的度数.
(2)、如图2所示, 是等腰直角 内一点,连接 , ,连接 .当 满足什么条件时, .请给出证明.