山东省菏泽市郓城县2020-2021学年八年级上学期期末数学试题
试卷更新日期：2021-11-09 类型：期末考试
一、单选题
-
1. 如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（ ）A、12米 B、13米 C、14米 D、15米2. 的平方根是（ ）A、4 B、±4 C、±2 D、-23. 若方程mx+ny=6的两个解是 ， ，则m，n的值为（ ）A、4，2 B、2，4 C、﹣4，﹣2 D、﹣2，﹣44. 用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象（如图所示），则所解的二元一次方程组是（ ）
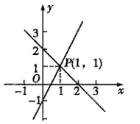A、 B、 C、 D、5. 已知小华上学期语文、数学、英语三科平均分为92分，他记得语文得了88分，英语得了95分，但他把数学成绩忘记了，你能告诉他应该是以下哪个分数吗？（ ）A、93 B、95 C、94 D、966. 某组7名同学在一学期里阅读课外书籍的册数分别是：14，12，13，12，17，18，16．则这组数据的众数和中位数分别是( )A、12，13 B、12，14 C、13，14 D、13，167. 如图，下列说法错误的是( )
A、因为∠BAD＋∠ADC＝180°，所以AB∥CD B、因为AB∥CD，所以∠BAC＝∠ACD C、因为∠ABD＝∠CDB，所以AD∥BC D、因为AD∥BC，所以∠BCA＝∠DAC8. 如果三角形的三个内角的度数比是2:3:4,则它是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、钝角或直角三角形二、填空题
-
9. 若点M（a，﹣1）与点N（2，b）关于y轴对称，则a+b的值是10. 当m=时，函数y=（2m－1）X 是正比例函数．11. 王老师把几本《数学大世界》给学生们阅读．若每人3本，则剩下3本；若每人5本，则有一位同学分不到书看，只够平均分给其他几位同学．则学生与书本的数量分别是；12. 已知样本数据 的方差为2，则 的方差是 ．13. 如图，已知 ， ，则 度
14. 用等腰直角三角板画 ，并将三角板沿 方向平移到如图所示的虚线处后绕点 逆时针方向旋转 ，则三角板的斜边与射线 的夹角 为 ．
三、解答题
-
15. 如图，在Rt△ABC中，∠ABC=90°，AB=16cm，正方形BCEF的面积为144cm2 ， BD⊥AC于点D，求BD的长.
16. 如果 的整数部分是a，小数部分是b，求 的值．17. 在平面直角坐标系中，点A关于y轴的对称点为点B，点B关于x轴的对称点为点C．
(1)、若点A的坐标为(1，2)，请你在给出的坐标系中画出ΔABC，设AB与y轴的交点为D，求 的值；(2)、若点A的坐标为(a，b)(ab≠0)，判断ΔABC的形状.18. 地表以下岩层的温度 ，随着所处的深度 的变化而变化，t与h在一定范围内近似成一次函数关系．(1)、根据下表，求 与 之间的函数关系式．温度
…
20
90
160
…
深度
…
0
2
4
…
(2)、求当岩层温度达到 时，岩层所处的深度为多少千米？19. 为迎接国庆，某市准备用灯饰美化红旗路，需采用 、 两种不同类型的灯笼共200个，且 型灯笼的个数是 型灯笼的 ．(1)、求 两种灯笼各需多少个；(2)、已知 两种灯笼的单价分别为40元、60元，则这次美化工程购置灯笼需多少费用？20. 一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车．已知过去两次租用这两种货车的情况如下表：第一次
第二次
甲种货车辆数（辆）
2
5
乙种货车辆数（辆）
3
6
累计运货吨数（吨）
15.5
35
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货，如果按每吨付运费30元计算，问货主应付运费多少元？
21. 某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：每人销售件数
1800
510
250
210
150
120
人数
1
1
3
5
3
2
(1)、求这15位营销人员该月销售量的平均数、中位数和众数；
(2)、假设销售负责人把每位营销员的月销售额定为320件，你认为是否合理，为什么？如不合理，请你制定一个较合理的销售定额，并说明理由．22. 王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%．现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示．
(1)、分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；(2)、试通过计算说明，哪个山上的杨梅产量较稳定？
