山东省东营市垦利区（五四制）2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 解分式方程 $\frac{2}{x + 1} + \frac{3}{x - 1} = \frac{6}{x^{2} - 1}$ ，分以下四步，其中错误的一步是（）.

A、方程两边分式的最简公分母是 $(x - 1) (x + 1)$ B、方程两边都乘以 $(x - 1) (x + 1)$ ，得整式方程 $2 (x - 1) + 3 (x + 1) = 6$ C、解这个整式方程，得 $x = 1$ D、原方程的解为 $x = 1$

查看试题解析
3. 如图，用一条宽相等的足够长的纸条，打一个结，如图1所示，然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE，其中∠BAE的度数是（）

A、90° B、108° C、120° D、135°

查看试题解析
4. 为了解某种电动汽车一次充电后行驶的里程数，抽检了 $10$ 辆车，对一次充电后行驶的里程数进行了统计，结果如图所示，则在这组数据中，众数和中位数分别是（）

A、 $220 ， 220$ B、 $210 ， 215$ C、 $210 ， 210$ D、 $220 ， 215$

查看试题解析
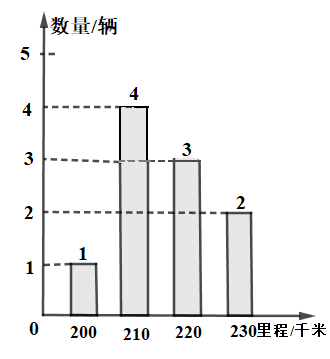5. 如图，将△ABC绕点B顺时针旋转50°得△DBE，点C的对应点恰好落在AB的延长线上，连接AD，下列结论不一定成立的是（）

A、AB=DB B、∠CBD=80° C、∠ABD=∠E D、△ABC≌△DBE

查看试题解析
6. 某校为了丰富校园生活，准备购进一批篮球和足球，其中篮球的单价比足球的单价多20元，李老师购买篮球花费900元，购买足球花费400元，结果购得篮球数量是足球数量的1.5倍，设购买足球数量是x个，则下列选项中所列方程正确的是（）

A、 $\frac{900}{x} = \frac{400}{1.5 x} + 20$ B、 $\frac{400}{x} = \frac{900}{1.5 x} + 20$ C、 $\frac{900}{1.5 x} = \frac{400}{x} + 20$ D、 $\frac{400}{1.5 x} = \frac{900}{x} + 20$

查看试题解析
7. 如图，在菱形 $A B C D$ 中， $A B = 5$ ， $B D = 6$ ， $D E ⊥ A B$ 于点E，则 $D E$ 的长为（）

A、4.8 B、5 C、9.6 D、10

查看试题解析
8. 若关于 $x$ 的分式方程 $\frac{m + 1}{x - 1} = 2$ 的解为非负数，则 $m$ 的取值范围是（）

A、 $m > - 3$ B、 $m \geq - 3$ C、 $m > - 3$ 且 $m \neq - 1$ D、 $m \geq - 3$ 且 $m \neq - 1$

查看试题解析
9. 如图， $O$ 是矩形 $A B C D$ 的对角线 $A C$ 的中点， $M$ 是 $C D$ 边的中点．若 $A B = 12$ ， $O M = \frac{9}{2}$ ，则线段 $O B$ 的长为（）

A、7 B、8 C、 $\frac{15}{2}$ D、 $\frac{16}{2}$

查看试题解析
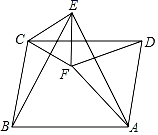
10. 如图所示，在平行四边形ABCD中，分别以AB、AD为边作等边△ABE和等边△ADF，分别连接CE，CF和EF，则下列结论，一定成立的个数是（）
①△CDF≌△EBC；②△CEF是等边三角形；③∠CDF＝∠EAF；④CE∥DF

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解： $m^{3} - 6 m^{2} + 9 m =$ ．

查看试题解析
12. 如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠BAD=127°，则∠BCE= ．

查看试题解析
13. 如图，小明从A点出发，沿直线前进8米后向左转45°，再沿直线前进8米，又向左转45°…照这样走下去，他第一次回到出发点A时，共走路程为米．

查看试题解析
14. 如果代数式m²+2m＝1，那么 $\frac{m^{2} + 4 m + 4}{m} \div \frac{m + 2}{m^{2}}$ 的值为．

查看试题解析
15. 跳远运动员李阳对训练效果进行测试5次跳远的成绩如下：7.9，7.6，7.8，7.7，8.0，（单位：m）这五次成绩的平均数为7.8m，方差为0.02．如果李阳再跳一次，成绩为7.8m．则李阳这6次跳远成绩的方差（填“变大”、“不变”或“变小”）．

查看试题解析
16. 如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长等于．

查看试题解析
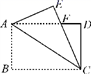17. 如图，点D、E分别是边AB、AC上的点，已知点F、G、H分别是DE、BE、BC的中点，连接FG、GH、FH，若BD=8，CE=6，∠FGH=90°，则FH长为．

查看试题解析
18. 如图，在 $△ A B C$ 中，已知AB=8，BC=6，AC=7，依次连接 $△ A B C$ 的三边中点，得到 $△ A_{1} B_{1} C_{1}$ ，再依次连接 $△ A_{1} B_{1} C_{1}$ 的三边中点，得到 $△ A_{2} B_{2} C_{2}$ ， $\cdot \cdot \cdot$ ，按这样的规律下去， $△ A_{2020} B_{2020} C_{2020}$ 的周长为．

查看试题解析

三、解答题

19.

(1)、解方程： $\frac{x}{3 x - 1} - 2 = \frac{1}{9 x - 3}$ ；

(2)、先化简： $(\frac{2 a^{2} - 2 a}{a^{2} - 2 a + 1} - 1) \div \frac{a^{2} + a}{a^{2} - 1}$ ，然后从﹣1，0，1，2中选一个合适的数作为a的值代入求值．

查看试题解析
20. 已知：△A₁B₁C₁三个顶点的坐标分别为A₁(﹣3，4)，B₁(﹣1，3)，C₁(1，6)，把△A₁B₁C₁先向右平移3个单位长度，再向下平移3个单位长度后得到△ABC，且点A₁的对应点为A，点B₁的对应点为B，点C₁的对应点为C．

⑴在坐标系中画出△ABC；

⑵画出△ABC关于原点O对称的△A₂B₂C₂；

⑶设点P在y轴上，且△APB与△ABC的面积相等，求点P的坐标．

查看试题解析
21. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：

（Ⅰ）图1中a的值为 ▲ ；

（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；

（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．

查看试题解析
22. 如图，在△ABC中，AB=AC，AD为∠BAC的平分线，AN为△ABC的外角∠BAM的平分线，BE⊥AN，垂足为点E．

(1)、求证：四边形ADBE是矩形．

(2)、连接DE，试判断四边形ACDE的形状，并证明你的结论．

查看试题解析
23. 阅读材料：若m²﹣2mn+2n²﹣8n+16=0，求m、n的值．
解：∵m²﹣2mn+2n²﹣8n+16=0，∴（m²﹣2mn+n²）+（n²﹣8n+16）=0
∴（m﹣n）²+（n﹣4）²=0，∴（m﹣n）²=0，（n﹣4）²=0，∴n=4，m=4．
根据你的观察，探究下面的问题：

(1)、已知x²+2xy+2y²+2y+1=0，求2x+y的值；

(2)、已知a﹣b=4，ab+c²﹣6c+13=0，求a+b+c的值．

查看试题解析
24. 复课返校后，为了拉大学生锻炼的间距，某学校决定增购适合独立训练的两种体育器材：跳绳和毽子，已知跳绳的单价比毽子的单价多4元，用1000元购买的跳绳个数和用800元购买的键子数量相同．

(1)、求跳绳和毽子的单价分别是多少元？

(2)、学校计划购买跳绳和毽子两种器材共400个，由于受疫情影响，商场决定对这两种器材打折销售，其中跳绳以八折出售，毽子以七五折出售，学校要求跳绳的数量不少于毽子数量的3倍，跳绳的数量不多于302根，请你求出学校花钱最少的购买方案．

查看试题解析
25. 如图一，在平行四边形ABCD中，AB⊥AC，AB=1，BC= $\sqrt{5}$ ，对角线AC，BD相交于O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．（所需图形须在备用图中画出）

(1)、试说明在旋转过程中，线段AF与EC总保持相等；

(2)、求证：当旋转角为90°时，四边形ABEF是平行四边形；

(3)、在旋转过程中，当EF⊥BD，旋转的角度小于180°时，求出此时绕点O顺时针旋转的度数．

查看试题解析