山东省东营市河口区（五四制）2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各分式中，是最简分式的是（）

A、 $\frac{x^{2} + y^{2}}{x + y}$ B、 $\frac{x^{2} - y^{2}}{x + y}$ C、 $\frac{x^{2} + x}{x y}$ D、 $\frac{x y}{y^{2}}$

查看试题解析
3. 下面关于平行四边形的说法中，错误的是（）

A、对角线互相平分的四边形是平行四边形 B、有一组对边平行，一组对角相等的四边形是平行四边形 C、有一组对边相等，一组对角相等的四边形是平行四边形 D、有两组对角相等的四边形是平行四边形

查看试题解析
4. 在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的( )

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
5. 如图所示， $△ A B C$ 中， $∠ C = 65 °$ ，将 $Δ A B C$ 绕点 $A$ 顺时针旋转后，得到 $Δ A B^{'} C^{'}$ ，且 $C^{'}$ 在边 $B C$ 上，则 $∠ B^{'} C^{'} B$ 的度数是（）

A、46° B、48° C、50° D、52°

查看试题解析
6. A，B两地相距48千米，一艘轮船从A地顺流航行至B地，又立即从B地逆流返回A地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x千米/时，则可列方程（）

A、 $\frac{48}{x + 4} + \frac{48}{x - 4} = 9$ B、 $\frac{48}{4 + x} + \frac{48}{4 - x} = 9$ C、 $\frac{48}{x}$ +4=9 D、 $\frac{96}{x + 4} + \frac{96}{x - 4} = 9$

查看试题解析
7. 有公共顶点A，B的正五边形和正六边形按如图所示位置摆放，连接AC交正六边形于点D，则∠ADE的度数为（　　）

A、144° B、84° C、74° D、54°

查看试题解析
8. 如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长度为（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析
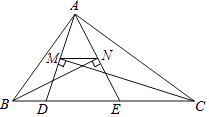9. 若关于 $x$ 的分式方程 $\frac{m}{2 x - 4} = \frac{1 - x}{2 - x} - 2$ 的根是正数，则实数 $m$ 的取值范围是（）.

A、 $m > - 4$ ，且 $m \neq 0$ B、 $m < 10$ ，且 $m \neq - 2$ C、 $m < 0$ ，且 $m \neq - 4$ D、 $m < 6$ ，且 $m \neq 2$

查看试题解析
10. 如图，在△ABC中，AB＝3，AC＝4，BC＝5，△ABD ， △ACE ， △BCF都是等边三角形，下列结论中：①AB⊥AC；②四边形AEFD是平行四边形；③∠DFE＝150°；④S_四边形_AEFD＝5．正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解：4m²﹣24m+36＝

查看试题解析
12. 一个 $n$ 边形的内角和等于外角和的2倍，则其边数 $n$ 为．

查看试题解析
13. 某公司要招聘职员，竞聘者需通过计算机、语言表达和写作能力测试，李丽的三项成绩百分制依次是70分，90分，80分，其中计算机成绩占 $50 %$ ，语言表达成绩占 $30 %$ ，写作能力成绩占 $20 %$ ，则李丽最终的成绩是分.

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中，点 $M$ 为边 $A D$ 上一点， $A M = 2 M D$ ，点 $E$ ，点 $F$ 分别是 $B M ， C M$ 中点，若 $E F = 6$ ，则 $A M$ 的长为．

查看试题解析
15. 若关于x的分式方程 $\frac{x + m}{x - 3} + \frac{3 m}{3 - x} = 3$ 有增根，则实数m的值为．

查看试题解析
16. 如图，△ABC的边长AB =3 cm，BC=4 cm，AC=2 cm，将△ABC沿BC方向平移a cm（a＜4 cm），得到△DEF，连接AD，则阴影部分的周长为cm．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ B A C = 45 °$ ， $A B = A C = 4$ ，点D是AB上一动点，以AC为对角线的所有平行四边形ADCE中，DE的最小值是．

查看试题解析
18. 如图，在平面直角坐标系中，将△ABC绕点A顺时针旋转到△AB₁C₁的位置，点B，O（分别落在点B₁ ， C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，再将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去，…，若点A(3，0)，B(0，4)，AB=5，则点B₂₀₂₁的坐标为．

查看试题解析

三、解答题

19.

(1)、解方程． $\frac{2}{x + 1} + \frac{5}{1 - x} = \frac{- 10}{x^{2} - 1}$ ．

(2)、先化简分式（ $\frac{a^{2} - 4}{a^{2} - 4 a + 4} - \frac{1}{a - 2}$ ）÷ $\frac{a + 1}{a^{2} - 2 a}$ ，然后在0，1，2中选一个你认为合适的a值，代入求值．

查看试题解析
20. 如图，在一个10×10的正方形网格中有一个△ABC，△ABC的顶点都在格点上．

(1)、在网格中画出△ABC向下平移4个单位，再向右平移6个单位得到的△A₁B₁C₁ ．

(2)、在网格中画出△ABC关于点P成中心对称得到的△A₂B₂C₂ ．

(3)、若可将△A₁B₁C₁绕点O旋转得到△A₂B₂C₂ ，请在正方形网格中标出点O，连接A₁A₂和B₁B₂ ，请直接写出四边形A₂B₂A₁B₁的面积．

查看试题解析

21. 某中学举行“中国梦”校园好声音歌手比赛，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，根据这10人的决赛成绩（满分为100分），制作了如下统计图：

(1)、根据上图提供的数据填空：

	平均数	中位数	众数	方差
初中部	*	85	$b$	70
高中部	85	$a$	100	*

$a$ 的值是， $b$ 的值是；

(2)、结合两队的平均数和中位数，分析哪个队的决赛成绩好；

(3)、根据题（1）中的数据，试通过计算说明，哪个代表队的成绩比较稳定？

查看试题解析

22. 如图，在▱ABCD中，点E在AD上，连接BE，DF∥BE交BC于点F，AF与BE交于点M，CE与DF交于点N．

(1)、求证：DE=BF；

(2)、求证：四边形MFNE是平行四边形．

查看试题解析
23. 把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．
如：①用配方法分解因式：a²+6a+8，

解：原式=a²+6a+8+1-1=a²+6a+9-1

=(a+3)²－1²=[(a+3)+1][(a+3)-1]=(a+4)(a+2)

②M=a²-2a－1，利用配方法求M的最小值．

解：a²-2a-1=a²-2a+1=(a-1)²-2

∵(a-b)²≥0，∴当a=1时，M有最小值-2．

请根据上述材料解决下列问题：

(1)、用配方法因式分解：x²+2x-3．

(2)、若M=2x²-8x，求M的最小值．

查看试题解析
24. “你怎么样，中国便是怎么样：你若光明，中国便不黑暗”。2019年，一场新冠肺炎疫情牵扯着人们的心灵，各界人士齐心协力，众志成城。针对资源急需问题，某医疗设备公司紧急复工，但受疫情影响，医用防护服生产车间仍有7人不能到厂生产，为了应对疫情，已复产的工人加班生产，由原来每天工作8小时增加到10小时，每小时完成的工作量不变原来每天能生产防护服 $800$ 套，现在每天能生产防护服650套．

(1)、求原来生产防护服的工人有多少人？

(2)、复工 $10$ 天后，未到的工人同时到岗加入生产，每天生产时间仍然为 $10$ 小时公司决定将复工后生产的防护服 $14500$ 套捐献给某地，则至少还需要生产多少天才能完成任务？

查看试题解析
25. 旋转变换在平面几何中有着广泛的应用．特别是在解（证）有关等腰三角形、正三角形、正方形等问题时，更是经常用到的思维方法，请你用旋转变换等知识，解决下面的问题．如图1，△ABC与△DCE均为等腰直角三角形，DC与AB交于点M，CE与AB交于点N．

(1)、以点C为中心，将△ACM逆时针旋转90°，画出旋转后的图形，并证明AM²+BN²=MN² ．

(2)、如图2，在四边形ABCD中，∠BAD=45°，∠BCD=90°，AC平分∠BCD，若BC=4，CD=3，则对角线AC的长度为多少？

查看试题解析