山东省德州市齐河县2020-2021学年八年级上学期期末数学试题(A)
试卷更新日期:2021-11-09 类型:期末考试
一、单选题
-
1. 下列图形,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果单项式 与 是同类项,那么这两个单项式的积是( )A、 B、 C、 D、3. 如图, , , , ,则 的度数是( )
2. 如果单项式 与 是同类项,那么这两个单项式的积是( )A、 B、 C、 D、3. 如图, , , , ,则 的度数是( ) A、105° B、115° C、125° D、130°4. 如图,作 关于直线对称的图形 ,接着 沿着平行于直线 的方向向下平移,在这个变换过程中两个对应三角形的对应点应具有的性质是( )
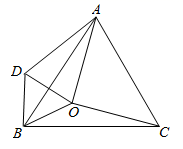
A、105° B、115° C、125° D、130°4. 如图,作 关于直线对称的图形 ,接着 沿着平行于直线 的方向向下平移,在这个变换过程中两个对应三角形的对应点应具有的性质是( )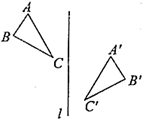 A、对应点连线相等 B、对应点连线互相平行 C、对应点连线垂直于直线 D、对应点连线被直线平分5. 如图,在等腰 中, , 垂直平分线 交 于点 ,交 于点 , 的垂直平分线 交 于点 ,交 于点 ,连接 , ,则 ( )
A、对应点连线相等 B、对应点连线互相平行 C、对应点连线垂直于直线 D、对应点连线被直线平分5. 如图,在等腰 中, , 垂直平分线 交 于点 ,交 于点 , 的垂直平分线 交 于点 ,交 于点 ,连接 , ,则 ( ) A、65° B、60° C、56° D、50°6. 计算 的结果是( )A、 B、 C、0.75 D、-0.757. 下列各式从左到右变形错误的是( )A、 B、 C、 D、8. 如图所示, , 均为正三角形,连接 , 交于点 , 与 交于点 , 与 交于点 ,则下面结论错误的是( )
A、65° B、60° C、56° D、50°6. 计算 的结果是( )A、 B、 C、0.75 D、-0.757. 下列各式从左到右变形错误的是( )A、 B、 C、 D、8. 如图所示, , 均为正三角形,连接 , 交于点 , 与 交于点 , 与 交于点 ,则下面结论错误的是( ) A、 B、 C、 D、9. 如图所示,阴影部分是边长为 的大正方形中剪去一个边长为 的小正方形后得到的图形,佳佳将阴影部分通过割拼,拼成了图①和图②两种新的图形,其中能够验证平方差公式的是( )
A、 B、 C、 D、9. 如图所示,阴影部分是边长为 的大正方形中剪去一个边长为 的小正方形后得到的图形,佳佳将阴影部分通过割拼,拼成了图①和图②两种新的图形,其中能够验证平方差公式的是( ) A、① B、② C、①②都能 D、①②都不能10. 如图,在正方形 中, , 是 上的一点且 ,连接 ,动点 从点 以每秒2个单位长度的速度沿 向终点 运动,设点 的运动时间为 秒,当 和 全等时, 的值是( )
A、① B、② C、①②都能 D、①②都不能10. 如图,在正方形 中, , 是 上的一点且 ,连接 ,动点 从点 以每秒2个单位长度的速度沿 向终点 运动,设点 的运动时间为 秒,当 和 全等时, 的值是( ) A、3.5 B、5.5 C、6.5 D、3.5或6.5
A、3.5 B、5.5 C、6.5 D、3.5或6.5二、填空题
-
11. 要使 的值和 的值互为相反数,则x的值是 .12. 图中有个三角形.
 13. 分解因式: .14. 如图所示,折叠直角三角形纸片的直角,使点 落在 上的点 处,已知 , ,则 的长是 .
13. 分解因式: .14. 如图所示,折叠直角三角形纸片的直角,使点 落在 上的点 处,已知 , ,则 的长是 . 15. 找规律: , , …根据上面的规律:当n为正整数时,得 .
15. 找规律: , , …根据上面的规律:当n为正整数时,得 .三、解答题
-
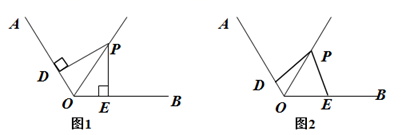
16. 化简:(1)、(2)、解方程:17. 先化简,再求值: ,其中 .18. 观察等式找规律: ; ; ; ;…(1)、根据以上规律写出第 个等式;(2)、根据你得出的结论计算右面这个式子的结果: ;(3)、若 ,求 的值.19. 沛沛沿一段笔直的人行道行走,边走边欣赏风景,在由 走到 的过程中,通过隔离带的空隙 ,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图, ,相邻两平行线间的距离相等 , 相交于 , 垂足为 .已知 米.请根据上述信息求标语 的长度.
 20. 如图,在 中, , , 垂直于 于点 , 是 的中点.
20. 如图,在 中, , , 垂直于 于点 , 是 的中点. (1)、求证: ;(2)、若 ,求 的长.21. 某学校利用暑假对操场进行塑胶跑道的建设,承包单位派甲队进行施工,计划用45天时间完成整个工程,当甲队工作3天后,承包单位接到通知,有一大型比赛要在该操场举行,要求比原计划提前14天完成这个工程,于是承包单位派遣乙队与甲队共同完成剩余工程,结果按通知要求如期完成整个工程.(1)、乙队单独工作完成整个工程需要多少天?(2)、若刚开始,由甲乙两队同时进行施工,完成整个工程需要多少天?
(1)、求证: ;(2)、若 ,求 的长.21. 某学校利用暑假对操场进行塑胶跑道的建设,承包单位派甲队进行施工,计划用45天时间完成整个工程,当甲队工作3天后,承包单位接到通知,有一大型比赛要在该操场举行,要求比原计划提前14天完成这个工程,于是承包单位派遣乙队与甲队共同完成剩余工程,结果按通知要求如期完成整个工程.(1)、乙队单独工作完成整个工程需要多少天?(2)、若刚开始,由甲乙两队同时进行施工,完成整个工程需要多少天?