山东省滨州市无棣县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 斐波那契螺旋线也称为“黄金螺旋线”，它是根据斐波那契数列画出米的螺旋曲线，科学家在自然界中发现存在许多斐波那契螺旋线图案．下列斐波那契螺旋线图案中属于轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 若一个三角形的三边长分别为3，7，x，则x的值可能是（）

A、6 B、3 C、2 D、11

查看试题解析
3. 三角形按边分类可以用集合来表示，如图所示，图中小椭圆圈里的A表示（）

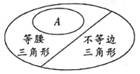A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形

查看试题解析
4. 下列计算中，结果是 $m^{8}$ 的是（）

A、 ${(m^{2})}^{4}$ B、 $m^{2} • m^{4}$ C、 $m^{12} \div m^{2}$ D、 $m^{2} + m^{4}$

查看试题解析
5. 如图是作 $Δ A B C$ 的作图痕迹，则此作图的已知条件是（）

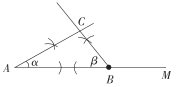A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角

查看试题解析
6. 关于分式 $\frac{2 m - 6 n}{3 m - 4 n}$ ，下列说法正确的是（）

A、分子、分母中的m、n均扩大2倍，分式的值也扩大2倍 B、分子、分母的中m扩大2倍，n不变，分式的值扩大2倍 C、分子、分母的中n扩大2倍，m不变，分式的值不变 D、分子、分母中的m、n均扩大2倍，分式的值不变

查看试题解析
7. 下列说法中，①面积相等的两个三角形全等：②周长相等的两个等边三角形全等：③有三个角对应相等的两个三角形全等：④有三边对应相等的两个三角形全等，错误的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. “三等分角”大约是在公元前五世纪由古希腊人提出来的．借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA， OB组成，两根棒在O点相连并可绕O转动，C点固定， $O C = C D = D E$ ，点D，E可在槽中滑动，若 $∠ B D E = 72^{°}$ ，则 $∠ C D E$ 的度数是（）

A、84° B、82° C、81° D、78°

查看试题解析
9. 对于① $(x + 2) (x - 1) = x^{2} + x - 2$ ，② $x - 4 x y = x (1 - 4 y)$ ，从左到右的变形，表述正确的是（）

A、都是因式分解 B、都是乘法运算 C、①是因式分解，②是乘法运算 D、①是乘法运算，②是因式分解

查看试题解析
10. 如图，已知 $A B + A C = 16$ ，点O为 $∠ A B C$ 与 $∠ A C B$ 的平分线的交点，且 $O D ⊥ B C$ 于D．若 $O D = 4$ ，则四边形ABOC的面积是（）

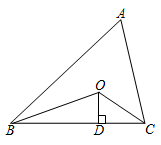A、36 B、32 C、30 D、64

查看试题解析
11. 若关于x的方程 $\frac{m - 1}{x - 1} = 2$ 的解为正数，则m的取值范围是（）

A、 $m > - 1$ B、 $m \neq 1$ C、 $m > 1$ D、 $m > - 1$ 且 $m \neq 1$

查看试题解析
12. 如图， $△ A B C$ 中， $∠ A B C = 45^{°}$ ， $C D ⊥ A B$ 于D，BE平分 $∠ A B C$ ，且 $B E ⊥ A C$ 于E，与CD相交于点F， $D H ⊥ B C$ 于H，交BE于G，下列结论：① $B D = C D$ ；② $A E = B G$ ；③ $2 C E = B F$ ；④ $A D + C F = B D$ ．其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 因式分解： $m^{3} n^{2} - m =$ ．

查看试题解析
14. 如图所示，要测量河两岸相对的两点 $A$ 、 $B$ 的距离，在 $A B$ 的垂线段 $B F$ 上取两点 $C$ 、 $D$ ，使 $B C = C D$ ，过 $D$ 作 $B F$ 的垂线 $D E$ ，与 $A C$ 的延长线交于点 $E$ ，若测得 $D E$ 的长为 $20$ 米，则河宽 $A B$ 长为米．

查看试题解析
15. 已知x^m＝ $\frac{1}{8}$ ，xⁿ＝16，则x^2m+n的值为.

查看试题解析
16. 一副直角三角板如上图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，则∠DBC＝°．

查看试题解析
17. 如图， $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 50^{°}$ ，AD是中线， $B E ⊥ A C$ ，垂足为E，AD与BE交于点F，则 $∠ B F A =$ ．

查看试题解析
18. 在平面直角坐标系中，将点 $P (3 ， - 2)$ 向右平移4个单位得到点 $P^{'}$ ，则点 $P^{'}$ 关于x轴的对称点的坐标为．

查看试题解析
19. 计算： $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times \dots \dots \times (1 - \frac{1}{10^{2}}) =$

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ A C B = 90^{°}$ ， $∠ B = 30^{°}$ ， $A C = 6$ ，P为BC边的垂直平分线DE上一个动点，则 $△ A C P$ 周长的最小值为．

查看试题解析

三、解答题

21. 计算：

(1)、 ${(\frac{1}{4})}^{- 2} + {(π - 2021)}^{0} - | 1 - 3 | + {(- 2)}^{3}$ ；

(2)、 $(a + b) \cdot (a^{2} - a b + b^{2}) + (a - b) \cdot (a^{2} + a b + b^{2})$ ．

查看试题解析
22.

(1)、计算： $\frac{x^{2}}{y} \div \frac{- y^{2}}{x} \cdot {(\frac{y}{- x})}^{2}$

(2)、如图，在 $△ A B C$ 中，AD是中线， $C E ⊥ A D$ 于点E， $B F ⊥ A D$ ，交AD的延长线于点F，求证：点D是线段EF的中点．

查看试题解析
23.

(1)、先化简，再求值： $(\frac{m + 2}{m^{2} - 2 m} + \frac{8}{4 - m^{2}}) \div \frac{m^{2} - 4}{m}$ ，其中m满足 $m^{2} + 4 m + 3 = 0$ ．

(2)、如图，在等边 $△ A B C$ 中，D．E分别在边BC、AC上，且 $D E / / A B$ ，过点E作 $E F ⊥ D E$ 交BC的延长线于点F．若 $C D = 3 cm$ ，求DF的长．

查看试题解析
24. 列方程解应用题：为了响应绿色环保的倡议，我县教体局提出了每个人都践行“双面打印，节约用纸”的口号．已知打印一份资料，如果用 $A 4$ 厚型纸单面打印，总质量为800克，将其全部改成双面打印，用纸将减少一半；如果用 $A 4$ 薄型纸双面打印，这份资料的总质量为320克，已知每页 $A 4$ 薄型纸比 $A 4$ 厚型纸轻0.8克，求 $A 4$ 薄型纸每页的质量（墨的质量忽略不计）．

查看试题解析
25. 图1是一个长为 $2 a$ 、宽为 $2 b$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

(1)、图2中的阴影部分的正方形的周长等于．

(2)、观察图2，请你写出下列三个代数式 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ，ab之间的等量关系为．

(3)、运用你所得到的公式，计算：若m、n为实数，且 $m n = - 3$ ， $m - n = 4$ ，试求 $m + n$ 的值．

(4)、如图3，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设 $A B = 8$ ，两正方形的面积和 $S_{1} + S_{2} = 26$ ，求图中阴影部分面积．

查看试题解析
26. 如图，在四边形ABCD中， $A B / / C D$ ， $∠ A B C$ 的平分线交CD的延长线于点E，F是BE的中点，连接CF并延长交AD于点G．

(1)、求证： $∠ B C G = ∠ D C G$ ．

(2)、若 $∠ C G D = 50^{°}$ ， $∠ A B C = 58^{°}$ ，求 $∠ A D E$ 的度数．

查看试题解析
27. 如图， $△ A B C$ 是边长为10的等边三角形，现有两点P、Q沿如图所示的方向分别从点A、点B同时出发，沿 $△ A B C$ 的边运动，已知点P的速度为每秒1个单位长度，点Q的运度为每秒2个单位长度，当点P第一次到达B点时，P、Q同时停止运动．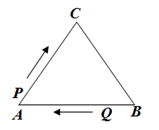

(1)、点P、Q运动几秒后，可得到等边三角形 $△ A P Q$ ？

(2)、点P、Q运动几秒后，P、Q两点重合？

(3)、当点P、Q在BC边上运动时，能否得到以PQ为底边的等腰 $△ A P Q$ ？如存在，请求出此时P、Q运动的时间．

查看试题解析