山东省滨州市惠民县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 小明有两根3cm、7cm的木棒，他想以这两根木棒为边做一个三角形，还需再选用的木棒长为（　　）

A、3cm B、4cm C、9cm D、10cm

查看试题解析
2. 运用图腾解释神话、民俗民风等是人类历史上最早的一种文化现象.下列图腾中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{(- 2) \times (- 3)} = \sqrt{- 2} \times \sqrt{- 3}$ C、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ D、 $\sqrt{6} \div \sqrt{3} = \sqrt{2}$

查看试题解析
4. 下列等式中，从左到右的变形是因式分解的是（）

A、 $m (a + b) = m a + m b$ B、 $3 x^{2} - 3 x + 1 = 3 x (x - 1) + 1$ C、 $x^{2} + 3 x + 2 = (x + 1) (x + 2)$ D、 $a^{2} + 4 a + 4 = {(a - 2)}^{2}$

查看试题解析
5. 2020年6月23日，中国第55颗北斗导航卫星成功发射，顺利完成全球组网．其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片，已实现规模化应用，22纳米=0.000000022米，将0.000000022用科学记数法表示为（）

A、22×10⁸ B、2.2×10^-8 C、0.22×10^-7 D、22×10^-9

查看试题解析
6. 如果把分式 $\frac{x + y}{x y}$ 中的x、y同时扩大为原来的2倍，那么该分式的值（　　）

A、不变 B、扩大为原来的2倍 C、缩小为原来的 $\frac{1}{2}$ D、缩小为原来的 $\frac{1}{4}$

查看试题解析
7. 下列式子正确的是（）

A、 $a^{2} - 4 b^{2} = (a + 4 b) (a - 4 b)$ B、 $a^{- 2} b^{2} \cdot {(a^{2} b^{- 2})}^{- 3} = \frac{b^{8}}{a^{8}}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 ${(- 1)}^{2020} + {(- 1)}^{0} = - 2$

查看试题解析
8. 已知△ABC ，两个完全一样的三角板如图摆放，它们的一组对应直角边分别在AB ， AC上，且这组对应边所对的顶点重合于点M ，点M一定在（）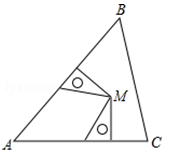

A、∠A的平分线上 B、AC边的高上 C、BC边的垂直平分线上 D、AB边的中线上

查看试题解析
9. 实数 $a$ ， $b$ 在数轴上对应的点的位置如图所示，化简 $| a | + \sqrt{{(a - b)}^{2}}$ 的结果是（）

A、 $- 2 a + b$ B、 $2 a - b$ C、 $- b$ D、 $b$

查看试题解析
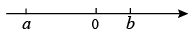10. 如图，已知∠MON及其边上一点A ，以点A为圆心，AO长为半径画弧，分别交OM ， ON于点B和C ，再以点C为圆心，AC长为半径画弧，恰好经过点B ，错误的结论是（）.

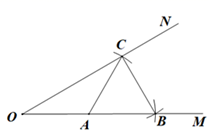A、 $S_{△ A O C} = S_{△ A B C}$ B、∠OCB＝90° C、∠MON＝30° D、OC＝2BC

查看试题解析
11. 关于 $x$ 的方程 $x + \frac{1}{x} = a + \frac{1}{a}$ 的两个解为 $x_{1} = a ， x_{2} = \frac{1}{a}$ ； $x + \frac{2}{x} = a + \frac{2}{a}$ 的两个解为 $x_{1} = a ， x_{2} = \frac{2}{a}$ ； $x + \frac{3}{x} = a + \frac{3}{a}$ 的两个解为 $x_{1} = a ， x_{2} = \frac{3}{a}$ ，则关于 $x$ 的方程 $x + \frac{10}{x - 1} = a + \frac{10}{a - 1}$ 的两个解为（）

A、 $x_{1} = a ， x_{2} = \frac{10}{a}$ B、 $x_{1} = a ， x_{2} = \frac{a + 8}{a - 1}$ C、 $x_{1} = a ， x_{2} = \frac{10}{a - 1}$ D、 $x_{1} = a ， x_{2} = \frac{a + 9}{a - 1}$

查看试题解析
12. 如图， $△ A B C$ 是等边三角形， $△ A B D$ 是等腰直角三角形，∠BAD=90°，AE⊥BD于点E．连CD分别交AE，AB于点F，G，过点A做AH⊥CD交BD于点H，则下列结论：①∠ADC=15°；②AF=AG；③AH=DF；④△ADF≌△BAH；⑤DF=2EH.其中正确结论的个数为（）

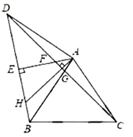A、5 B、4 C、3 D、2

查看试题解析

二、填空题

13. 如果 $\frac{\sqrt{x - 3}}{x - 1}$ 有意义，那么 $x$ 的取值范围是．

查看试题解析
14. 若 $3^{x} = 4$ ， $9^{y} = 7$ ，则 $3^{x - 2 y}$ 的值为．

查看试题解析
15. 若多项式 $x^{2} + 2 (3 - m) x + 25$ 是完全平方式，则 $m$ 的值为．

查看试题解析
16. 若最简二次根式 $\sqrt{4 a - 1}$ 和 $\sqrt[a - 1]{3 b + 5}$ 可以合并，则 $a^{- b} =$ ．

查看试题解析
17. 小强在做分式运算与解分式方程的题目时经常出现不符合题意，于是他在整理错题时，将这部分内容进行了梳理，如图所示：

请你帮小强在图中的括号里补写出“通分”和“去分母”的依据分别是：和

查看试题解析
18. 如图，点P是∠AOB内任意一点，且∠AOB=40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为．

查看试题解析
19. 若分式方程 $\frac{x}{x - 4} = 2 + \frac{a}{x - 4}$ 的解为正数，则a的取值范围是．

查看试题解析
20. 如图，直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ 于点 $D$ ， $A F$ 平分 $∠ C A B$ 交 $C D$ 于点 $E$ ，交 $B C$ 于点 $F$ ， $E G // A B$ 交 $C B$ 于点 $G$ ， $F H ⊥ A B$ 于 $H$ ，以下4个结论：① $∠ A C D = ∠ B$ ；② $△ C E F$ 是等边三角形；③ $C D = F H + D E$ ；④ $B G = C E$ 中正确的是（将正确结论的序号填空）

查看试题解析

三、解答题

21.

(1)、计算：① $\sqrt{8} + | 1 - \sqrt{2} | + {(\frac{1}{2})}^{- 1} - 2020^{0}$ ；
② ${(2 \sqrt{3} - 1)}^{2} - (\sqrt{3} + 2) (\sqrt{3} - 2)$ ．

(2)、先化简； $(\frac{a + 7}{a - 1} - \frac{2}{a + 1}) \div \frac{a^{2} + 3 a}{a^{2} - 1}$ ，再从-3、-2，-1、0、1中选一个合适的数作为 $a$ 的值代入求值．

查看试题解析
22. 如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．

(1)、求证：△ACD≌△CBE；

(2)、若AD=12，DE=7，求BE的长．

查看试题解析
23. 如图，在平面直角坐标系 xOy 中，△ABC 的三个顶点的坐标分别是 A(2，3)，B(1，0)，C(1，2).

(1)、在图中画出△ABC 关于 y 轴对称的 $△ A_{1} B_{1} C_{1}$

(2)、直接写出 $A_{1} 、 B_{1} 、 C_{1}$ 三点的坐标：
$A_{1}$ ()， $B_{1}$ ()， $C_{1}$ ()；

(3)、如果要使以 B、C、D 为顶点的三角形与△ABC 全等，直接写出所有符合条件的点 D 坐标.

查看试题解析
24. 列方程或列方程组解应用题.
老京张铁路是1909年由“中国铁路之父”詹天佑主持设计建造的中国第一条干线铁路，全长约210千米，用“人”字形铁轨铺筑的方式解决了火车上山的问题．京张高铁是2022年北京至张家口冬奥会的重点配套交通基础设施，全长约175千米，预计2019年底建成通车．京张高铁的预设平均速度将是老京张铁路的5倍，可以提前5个小时到达，求京张高铁的平均速度．

查看试题解析
25.

(1)、计算： $(a + 2) (a^{2} - 2 a + 4) =$ ．
$(2 x + y) (4 x^{2} - 2 x y + y^{2})$ $=$ ．

(2)、上面的整式乘法计算结果很简洁，你又发现一个新的乘法公式，请用含a、b的字母表示：；

(3)、下列各式能用你发现的乘法公式计算的是（）

A、 $(a + 3) (a^{2} - 3 a + 9)$ B、 $(2 m + n) (2 m^{2} + 2 m n + n^{2})$ C、 $(4 - x) (16 + 4 x - x^{2})$ D、 $(m - n) (m^{2} + 2 m n + n^{2})$

(4)、利用所学知识以及（2）所得等式，化简代数式 $\frac{m^{3} + n^{3}}{m^{2} - mn + n^{2}} \div \frac{m^{2} - n^{2}}{m^{2} - 2 mn + n^{2}}$ ．

查看试题解析
26. （知识生成）
我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式，例如图1可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，基于此，请解答下列问题：

(1)、根据图2，写出一个代数恒等式：．

(2)、利用（1）中得到的结论，解决下面的问题：若 $a + b + c = 10$ ， $a b + a c + b c = 35$ ，则 $a^{2} + b^{2} + c^{2} =$ ．

(3)、小明同学用图3中 $x$ 张边长为 $a$ 的正方形， $y$ 张边长为 $b$ 的正方形， $z$ 张宽、长分别为 $a$ 、 $b$ 的长方形纸片拼出一个面积为 $(3 a + b) (a + 3 b)$ 长方形，则 $x + y + z =$ ．

(4)、（知识迁移）
事实上，通过计算几何图形的体积也可以表示一些代数恒等式，图4表示的是一个边长为 $x$ 的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据图4中图形的变化关系，写出一个代数恒等式：．

查看试题解析
27.

(1)、（问题提出）（1）如图， $△ A B C$ 与 $△ A D E$ 均是顶角为 $40 °$ 的等腰三角形， $B C$ 、 $D E$ 分别是底边，求证： $B D = C E$ ；

(2)、
（类比延伸）如图， $△ A C B$ 与 $△ A E D$ 均为等边三角形，点 $B$ 、 $D$ 、 $E$ 在同一直线上，连接 $C E$ ．填空： $∠ A E C$ 的度数为；线段 $E C$ 与 $B D$ 之间的数量关系为．

(3)、
（拓展研究）如图， $△ A C B$ 与 $△ A E D$ 均为等腰直角三角形， $∠ C A B = ∠ E A D = 90 °$ ，点 $B$ 、 $D$ 、 $E$ 在同一直线上， $A M ⊥ D E$ 于点 $M$ ，连接 $C E$ ．请求出 $∠ B E C$ 的度数及线段 $A M$ 、 $C E$ 、 $B E$ 之间的数量关系，并说明理由．

查看试题解析