内蒙古自治区乌海市海勃湾区2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为（）

A、 0.215×10⁸ B、2.15×10⁷ C、2.15×10⁶ D、21.5×10⁶

查看试题解析
3. 下列运算正确的是（）

A、（﹣2a³）²＝4a⁶ B、a²•a³＝a⁶ C、3a+a²＝3a³ D、（a﹣b）²＝a²﹣b²

查看试题解析
4. 若 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 的平均数为4， $x_{5}$ ， $x_{6}$ ， $x_{7}$ ， $\cdot \cdot \cdot$ ， $x_{10}$ 的平均数为6，则 $x_{1}$ ， $x_{2}$ ， $\cdot \cdot \cdot$ ， $x_{10}$ 的平均数为（）

A、5 B、4.8 C、5.2 D、8

查看试题解析
5. 如图1，已知 $∠ A B C$ ，用尺规作它的角平分线．
如图2，步骤如下，

第一步：以B为圆心，以a为半径画弧，分别交射线 BA ， BC 于点D，E；

第二步：分别以D，E为圆心，以b为半径画弧，两弧在 $∠ A B C$ 内部交于点P；

第三步：画射线 BP ．射线 BP 即为所求．

下列正确的是（）

A、a，b均无限制 B、 $a > 0$ ， $b > \frac{1}{2} D E$ 的长 C、a有最小限制，b无限制 D、 $a \geq 0$ ， $b < \frac{1}{2} D E$ 的长

查看试题解析
6. “数学是将科学现象升华到科学本质认识的重要工具”，比如在化学中，甲烷的化学式CH₄ ，乙烷的化学式是C₂H₆ ，丙烷的化学式是C₃H₈ ， …，设碳原子的数目为n（n为正整数），则它们的化学式都可以用下列哪个式子来表示（　　）

A、C_nH_2n+2 B、C_nH_2n C、C_nH_2n_﹣₂ D、C_nH_n+3

查看试题解析
7. 如图，正八边形ABCDEFGH中，∠EAG大小为（）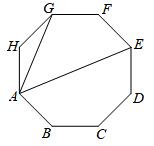

A、30° B、40° C、45° D、50°

查看试题解析
8. 如图，ABCD的对角线AC、BD相交于点O，EF、GH过点O，且点E、H在边AB上，点G、F在边CD上，向▱ABCD内部投掷飞镖（每次均落在▱ABCD内，且落在▱ABCD内任何一点的机会均等）恰好落在阴影区域的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
9. 用三个不等式 $a > b$ ， $a b > 0$ ， $\frac{1}{a} < \frac{1}{b}$ 中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
10. 设a，b是方程x²+x-2009=0的两个实数根，则a²+2a+b的值为（　　）

A、2006 B、2007 C、2008 D、2009

查看试题解析
11. 如图，将△ABC绕点C顺时针旋转得到△DEC ，使点A的对应点D恰好落在边AB上，点B的对应点为E ，连接BE ，下列四个结论：
①AC＝AD；②AB⊥EB；③BC＝EC；④∠A＝∠EBC；

其中一定正确的是（）

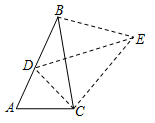A、①② B、②③ C、③④ D、②③④

查看试题解析
12. 如图所示，已知二次函数y＝ax²+bx+c的图象与x轴交于A ， B两点，与y轴交于点C ， OA＝OC ，对称轴为直线x＝1，则下列结论：①abc＜0；②a+ $\frac{1}{2}$ b+ $\frac{1}{4}$ c＞0；③ac+b+1＝0；④2+c是关于x的一元二次方程ax²+bx+c＝0的一个根．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 如图，若 $x = \sqrt{5}$ ，则表示 $\frac{x^{2} - 2 x + 1}{x} \div (1 - \frac{1}{x})$ 的值的点落在（填序号）

查看试题解析
14. 不等式组 ${\begin{array}{l} 2 - x \geq 0 \\ 2 x > x - 1 \end{array}$ 的最小整数解是.

查看试题解析
15. 代数式2a²-b=7，则10-4a²+2b的值是

查看试题解析
16. 已知：如图是由若干个大小相同的小正方体所搭成的几何体从正面、左面和上面看到的形状图，则搭成这个几何体的小正方体的个数是．

查看试题解析
17. 如图，在菱形ABCD中，对角线AC，BD交于点O，∠ABC=60°，AB=2，分别以点A、点C为圆心，以AO的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为．（结果保留 $π$ ）

查看试题解析
18. 如图所示的网格是正方形网格，则 $∠ P A B ＋ ∠ P B A$ ＝°（点A，B，P是网格线交点）.

查看试题解析
19. 如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为 $\overset{⌢}{A C}$ 上的动点，点M，N，P分别是AD，DC，CB的中点．若⊙O的半径为4，则PN+MN的长度的最大值是．

查看试题解析
20. 在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．
对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是．

查看试题解析

三、解答题

21. 为了全面建设“资源节约型、环境友好型”两型社会，我国正全力推进垃圾分类工作．垃圾分类通过分类投放、分类收集，把有用物资从垃圾中分离出来重新回收、利用，变废为宝．既提高垃圾资源利用水平，又可减少垃圾处置量．它是实现垃圾减量化和资源化的重要途径和手段．为了促进学生的垃圾分类的意识与行动，市教育局决定开展“垃圾分类知识竞赛”活动．某校团委为了落实此次活动，组织全校5000名学生进行了“垃圾分类知识竞赛”初赛活动，并随机抽取了部分初赛同学的成绩，整理并绘制成如图两个图表（部分末完成）．请你根据表中提供的信息，解答问题．

分数段	频数	频率
60≤x＜70	30	0.1
70≤x＜80	90	n
80≤x＜90	m	0.4
90≤x＜100	60	0.2

(1)、此次调查的样本容量为；m＝；n＝；

(2)、补全频数分布直方图；

(3)、已知全校共有四名同学均取得100分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校团委将从这四名同学中随机选出两名参加市级比赛，请用列举法或树状图法求甲、乙两名同学都被选中的概率．

查看试题解析

22. 交通安全是社会关注的热点问题，安全隐患主要是超速和超载．某中学八年级数学活动小组的同学进行了测试汽车速度的实验．如图，先在笔直的公路1旁选取一点P，在公路1上确定点O、B，使得PO⊥l，PO＝100米，∠PBO＝45°．这时，一辆轿车在公路1上由B向A匀速驶来，测得此车从B处行驶到A处所用的时间为3秒，并测得∠APO＝60°．此路段限速每小时80千米，试判断此车是否超速？请说明理由（参考数据： $\sqrt{2}$ ＝1.41， $\sqrt{3}$ ＝1.73）．

查看试题解析
23. 为迎接国庆节，某商店购进了一批成本为每件30元的纪念商品．经调查发现，该商品每天的销售量 $y$ （件 $)$ 与销售单价 $x$ （元 $)$ 满足一次函数关系，其图象如图所示．

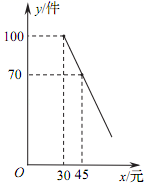(1)、求该商品每天的销售量y与销售单价x的函数关系式；

(2)、若商店按不低于成本价，且不高于60元的单价销售，则销售单价定为多少，才能使销售该商品每天获得的利润 $w$ （元 $)$ 最大？最大利润是多少？

查看试题解析
24. 如图，在⊙O中，点D为AB的中点，点P为半径OC延长线上一点，连结AC ， AP ，且AC平分∠PAB ．

(1)、求证：PA是⊙O的切线；

(2)、若AB平分OC ，且⊙O的半径为2，求PA的长度．

查看试题解析
25. 如图1，E是正方形ABCD中CD边上的一点，以点A为中心，把 $△ A D E$ 顺时针旋转α后，得到 $△ A B G$ .

(1)、求α的值；

(2)、当点F在BC上，且∠EAF=45°，连接EF（如图2），求证：BF+DE=EF；

(3)、在（2）的前提下，连接BD，分别交AE，AF于M，N两点（如图3），试判断线段BN，MN，DM三者的关系式，请给出证明.

查看试题解析
26. 已知：如图，抛物线y=ax²+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．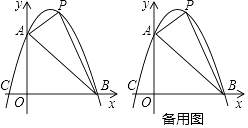

(1)、求抛物线的解析式；

(2)、当点P运动到什么位置时，△PAB的面积有最大值？

(3)、过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．

查看试题解析