内蒙古自治区呼和浩特市2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件是必然事件的是（）

A、经过有交通信号灯的路口，遇到红灯 B、射击运动员射击一次，命中靶心 C、从一定高度落下的图钉，落地后钉尖朝下 D、通常温度降到0℃以下，纯净的水会结冰

查看试题解析
2. 把点 $P (x ， y)$ 绕原点顺时针旋转270°，点 $P$ 的对应点的坐标是（）

A、 $(y ， - x)$ B、 $(- x ， - y)$ C、 $(- y ， x)$ D、 $(x ， y)$

查看试题解析
3. 如图， $P A$ ， $P B$ 是 $⊙ O$ 的切线， $A$ ， $B$ 为切点， $A C$ 是 $⊙ O$ 的直径， $∠ B A C = 25.5 °$ ，则 $∠ P$ 的度数为（）

A、52° B、51° C、61° D、64.5°

查看试题解析
4. 函数 $y = x^{2} + \frac{1}{\sqrt{- x}}$ 的图象上的点 $P (x ， y)$ 一定在第（）象限

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 半径为2的圆内接正六边形的边心距的长是（）

A、2 B、1 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 如图， $⊙ O$ 的直径 $C D = 10 cm$ ， $A B$ 是 $⊙ O$ 的弦， $A B ⊥ C D$ ，垂足为 $M$ ， $O D ： O M = 5 ： 3$ ，则 $A B$ 的长为（）

A、 $6 cm$ B、 $\sqrt{91} cm$ C、 $8 cm$ D、 $4 cm$

查看试题解析
7. 如图， $A B = 5$ ， $O$ 是 $A B$ 的中点， $P$ 是以点 $O$ 为圆心， $A B$ 为直径的半圆上的一个动点（点 $P$ 与点 $A$ ， $B$ 可以重合），连接 $P A$ ，过 $P$ 作 $P M ⊥ A B$ 于点 $M$ ，设 $A P = x$ ，则 $A M = \frac{1}{5} x^{2}$ ，令 $y = A P - A M$ ，下列图象中，能表示 $y$ 与 $x$ 的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 已知二次函数 $y = (2 - a) x^{2} + (a + 2) x - 1$ ，当 $x$ 取互为相反数的任意两个实数值时，对应的函数值 $y$ 总相等，则关于 $x$ 的一元二次方程 $(2 - a) x^{2} + (a + 2) x - 1 = 0$ 的两根之积为（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{4}$ C、－1 D、0

查看试题解析
9. 用一个圆心角为120°，半径为4的扇形，做一个圆锥的侧面，则这个圆锥的全面积（侧面与底面面积的和）为（）

A、 $\frac{56 π}{3}$ B、 $\frac{64 π}{3}$ C、 $\frac{56 π}{9}$ D、 $\frac{64 π}{9}$

查看试题解析
10. 下列结论中：① $△ A B C$ 的内切圆半径为 $r$ ， $△ A B C$ 的周长为 $L$ ，则 $△ A B C$ 的面积是 $\frac{1}{2} L r$ ；②同时抛掷两枚质地均匀的硬币，两枚硬币全部正面向上的概率为 $\frac{1}{2}$ ；③圆内接平行四边形是矩形；④无论 $p$ 取何值，方程 $(x - 3) (x - 2) - p^{2} = 0$ 总有两个不等的实数根．其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 把一枚质地均匀的骰子先后抛掷两次，将“两次抛掷骰子所得点数相同”记为事件 $A$ ，则 $P (A) =$ ．

查看试题解析
12. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，若 $∠ A D C = 80 °$ ，则 $∠ A B C$ 的度数是．

查看试题解析
13. 关于 $x$ 的方程 $x^{2} + 10 x + 9 = 0$ 的实数根为．

查看试题解析
14. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则 $y > 0$ 时，对应的 $x$ 的取值范围为．

查看试题解析
15. 在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感．按此比例，如果雕像的高为 $2 m$ ，设雕像下部高为 $x m$ ，则可得到方程．

查看试题解析
16. 已知 $(- 3 ， y_{1})$ ， $(- 2 ， y_{2})$ ， $(1 ， y_{3})$ 是抛物线 $y = - 3 x^{2} - 12 x + m$ 上的点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是.

查看试题解析
17. 已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5，则在一定时间段内，由该元件组成的图示电路 $A$ ， $B$ 之间，电流能够正常通过的概率是．

查看试题解析
18. 下列四个二次函数：① $y = x^{2}$ ，② $y = - 2 x^{2}$ ，③ $y = \frac{1}{2} x^{2}$ ，④ $y = 3 x^{2}$ ．其中抛物线开口从大到小的排列顺序是（填序号即可）．

查看试题解析
19. 下列说法中正确的说法的序号是．
①367人中至少有两人是同月同日生；②某商场抽奖活动的中奖率为1‰，说明每抽1000张奖券，一定有一张能中奖；③“打开电视机，正在播放《动物世界》”是随机事件；④“明天降雨的概率是80%”表示明天有80%的时间降雨．

查看试题解析
20. 二次函数 $y = x^{2} + b x$ 的图象如图，对称轴为直线 $x = 1$ ．若关于 $x$ 的一元二次方程 $x^{2} + b x - t = 0$ （ $t$ 为实数）在 $- 1 < x < 4$ 的范围内解，则 $t$ 的取值范围是．

查看试题解析

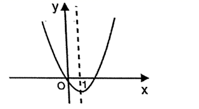
三、解答题

21. 按要求解下列方程

(1)、 $3 x^{2} + 6 x - 4 = 0$ （配方法）

(2)、 ${(2 x - 1)}^{2} = x^{2} + 6 x + 9$ （因式分解法）

查看试题解析
22. 如图， $△ A B C$ 在平面直角坐标系内，顶点的坐标分别为 $A (- 4 ， 4)$ ， $B (- 2 ， 5)$ ， $C (- 2 ， 1)$ ．

(1)、平移 $△ A B C$ ，使点 $C$ 移到点 $C_{1} (- 2 ， - 4)$ ，画出平移后的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $B_{1}$ 的坐标；

(2)、画出与 $△ A B C$ 关于原点对称的图形．

查看试题解析
23. 已知关于 $x$ 的一元二次方程 $m x^{2} - 4 x - 5 = 0$ ．

(1)、求证：当 $m > 0$ 时，方程一定有两个不相等的实数根；

(2)、已知 $x = n$ 是它的一个实数根，若 $m n^{2} - 4 n + m = 3 + m^{2}$ ，求 $m$ 的值．

查看试题解析
24. 如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至 $CE'F'D'$ ，旋转角为 .

(1)、当点 $D$ ′恰好落在EF边上时，求旋转角的值；

(2)、如图2，G为BC的中点，且0°＜＜90°，求证： $GD' = E'D$ ；

(3)、小长方形CEFD绕点C顺时针旋转一周的过程中， $Δ DCD'$ 与 $Δ CBD'$ 能否全等？若能，直接写出旋转角的值；若不能，说明理由.

查看试题解析
25. 已知二次函数 $y = \frac{1}{4} x^{2} - 6 x + c + 27$ ．

(1)、求证：当 $c = 10$ 时，任意实数 $a$ ，对应的函数值 $\frac{1}{4} a^{2} - 6 a + c + 27 \geq 1$ ；

(2)、该函数图象是否可以通过函数 $y = \frac{1}{4} x^{2} - 6 x$ 的图象平移得到，如果能，请写出变化过程．

查看试题解析
26. 如图， $A B$ 是半圆 $O$ 的直径，点 $C$ 是半圆上不同于 $A$ ， $B$ 的一动点，在弧 $B C$ 上取点 $D$ ，使 $∠ D B C = ∠ A B C$ ， $D E$ 为半圆 $O$ 的切线，过点 $B$ 作 $B F ⊥ D E$ 于点 $F$ ．

(1)、求证： $∠ D B F = 2 ∠ C A D$ ；

(2)、连接 $O C$ ， $C D$ ．探究：当 $∠ C A B$ 等于多少度时，四边形 $C O B D$ 为菱形，并且写出证明过程．

查看试题解析